Aurélie 01 / 05
approche de la seconde loi de Newton ; variation du vecteur vitesse

Google

Approche de la seconde loi de Newton

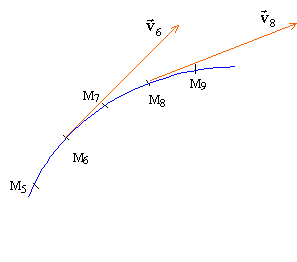
On enregistre, à intervalles de temps réguliers t = 20 ms, les positions successives da centre d'un palet autoporteur sur une table horizontale. L'enregistrement obtenu est représenté ci-dessous réduit à l'échelle 1/5 :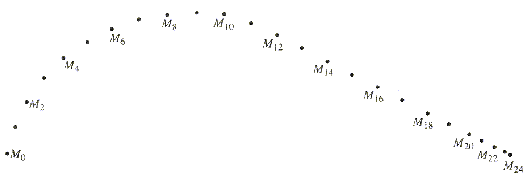

 

  1. Déterminer en m.s-1 la valeur v6 de la vitesse du point dans la position M6 .Représenter sur l'enregistrement le vecteur vitesse v6 à l'échelle 1 cm pour 0,5 m.s-1. M5M6 = 1 cm ; M6M7 = 1,2 cm ; (mesures faites sur le schéma)
  2. Même question au point M8. M7M8 = 0,9 cm ; M8M9 = 1,1 cm ; (mesures faites sur le schéma)
  3. Représenter sur l'enregistrement la variation du vecteur vitesse au point M7. Conclure quant à la somme vectorielle des forces appliquées sur le solide en M7.
corrigé
Le vecteur vitesse est tangent à la trajectoire et a le sens du mouvement.

au point M6, la valeur du vecteur vitesse v6 est égale à la vitesse moyenne sur le trajet M5M7.

v6 = (M5M6 + M6M7) / (2t)

t= 0,02 s ; M5M6 = 0,01 m et M6M7= 0,012 m.

en tenant compte de l'échelle 1/5 : M5M6 = 0,05 m et M6M7= 0,06 m.

v6 = (0,05+0,06)/ 0,04 = 2,75 m/s. ( soit une flèche de 5,4 cm de long)

au point M8, la valeur du vecteur vitesse v8 est égale à la vitesse moyenne sur le trajet M7M9.

v8 = (M7M8 + M8M9) / (2t)

t= 0,02 s ; M7M8 = 0,009 m et M8M9= 0,011 m.

en tenant compte de l'échelle 1/5 : M7M8 = 0,045 m et M8M9 = 0,055 m.

v6 = (0,045+0,055)/ 0,04 = 2,5 m/s. ( soit une flèche de 5 cm de long)

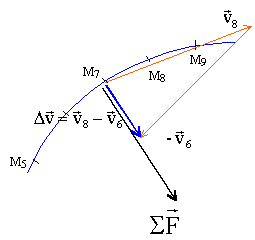
Le vecteur somme des forces est colinéaire et de même sens que le vecteur variation du vecteur vitesse au point M7. Il s'agit d'une approche de la seconde loi de Newton.

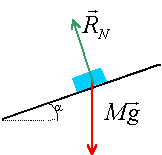
Une luge de masse m = 8,0 kg est lâchée sans vitesse initiale en haut d'une piste verglacée faisant un angle de 12° avec l'horizontale. Elle prend alors un mouvement de translation rectiligne accéléré suivant la ligne de plus grande pente. On prend g=9,8 N.kg-1 et on néglige tous les frottements.

  1. Faire le bilan des forces agissant sur la luge.
  2. Quels sont la direction et le sens du vecteur variation du vecteur vitesse du centre d'inertie de la luge pendant une petite durée ?
  3. En déduire la direction et le sens de la somme des forces agissant sur la luge.
  4. Calculer la valeur de la réaction de la piste.
corrigé
Les forces sont le poids, vertical, vers le bas, valeur P= mg et la réaction du support notée RN, perpendiculaire au support en absence de frottement, dirigée vers le haut.

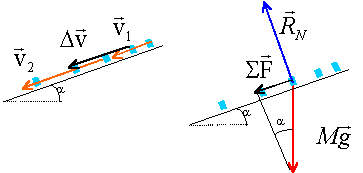
Le vecteur vitesse est tangent à la trajectoire ( donc parallèle au plan incliné), a le sens du mouvement. La vitesse augmente pendant la descente. La variation du vecteur vitesse est colinéaire au plan incliné et dirigé vers le bas du plan.

Le vecteur somme vectorielle des forces et colinéaire au vecteur variation de vitesse.

Le poids de la luge est P=mg soit 8 *9,8 = 78,4 N.

RN= P*cos 12 = 76,7 N

retour -menu