Aurélie dec 04
Devoir première S

théorème de l'énergie cinétique ; conductimétrie

d'après le site de sciences physiques d'Isabelle Tarride

Google

Une skieuse remonte une pente à vitesse constante. La piste est rectiligne, elle fait un angle constant a = 10° avec l'horizontale et mesure L = 300 m de long. Elle est aussi verglacée, ce qui permet de négliger les frottements. La tige du remonte-pente fait un angle b = 30° avec la direction de la piste. La force exercée par le remonte-pente sur la skieuse est constante.La masse de la skieuse et de son équipement est m = 60 kg. On prendra g = 9,8 N.kg-1.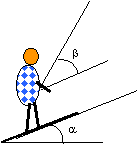

 

  1. Quelles sont les caractéristiques connues de toutes les forces s'exerçant sur le système {skieuse + équipement}. Préciser celles dont on ne connaît pas la valeur à priori ? Représenter ces forces sur un schéma.
  2. Quelle est la relation liant les forces appliquées au système ? Justifier en nommant et en énonçant la loi appropriée.
  3. Calculer le travail de ces forces sur le déplacement L.
  4. Énoncer le théorème de l'énergie cinétique et l'appliquer pour calculer la valeur d'une des forces.
  5. Arrivée en haut, la skieuse se laisse glisser sans vitesse initiale sur une piste rectiligne verglacée inclinée d'un angle d = 20° avec l'horizontale. Quelle est sa vitesse au bout de 100 m de descente ?
corrigé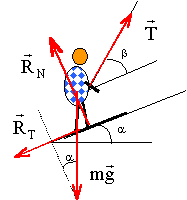

Le poids P , vertical, vers le bas, valeur P=mg= 60*9,8 = 588 N

L'action du plan R, perpendiculaire au plan en absence de frottement, valeur RN= mg cos a = 60*9,8*cos 10 = 579 N

dans le cas présent RT est nulle ( piste bien glacée, frottement quasiment nul)

Tension T de la perche, dirigée suivant la perche, valeur T inconnue.

Mouvement rectiligne et uniforme ( valeur de la vitesse constante) : d'après le principe d'inertie, les forces se compensent et le système est pseudo-isolé.

Principe d'inertie " dans un référentiel galiléen, si un solide est pseudo-isolé alors soit il est à l'état de repos,s oit son centre d'inertie est animé d'un mouvement rectiligne uniforme".

RN, perpendiculaire à la vitesse ne travaille pas.

le travail du poids est résistant en montée W(P) A--> B = -mg AB sin a = -mg L sin a= -60*9,8*300 sin 10 = -30 630 J .

le travail de la tension de la perche est moteur : W(T) A--> B = T AB cos b = T L cos b = T*300 cos 30 = 259,8 T.

Le système étant pseudo-isolé, l'énergie cinétique du système ne varie pas et en conséquence la somme algébrique des travaux des forces est nulle :

259,8 T-30630 = 0 soit T= 118 N.

th énergie cinétique : " la variation de l'énergie cinétique d'un système (S) entre deux dates t1 et t2 est égale à la somme des travaux des forces appliquées au système durant des deux dates ".

Appliquer le théorème de l'énergie cinétique lors de la descente:

départ : altitude h = longueur de la descente rectiligne*sin b =100 sin 20 = 34,2 m ; vitesse nulle)

arrivée : altitude choisie comme origine ; vitesse v

DEc= ½mv²-0 = ½mv²

La skieuse est soumise à son poids et à l'action du plan perpendiculaire au plan ( absence de frottement)

Seul le poids travaille et ce travail est moteur en descente

W(P) A--> B = mg AB sin d = 60*9,8*100*sin 20 = 20 111 J

½mv² = 20 111 soit v² = 20 111*2 / 60 = 670,3 et v = racine carrée (670,3) = 25,9 m/s.

 

  1. L'ion borate BO2- est une base selon Brönsted. Quel est son acide conjugué ? Écrire la demi-équation acido-basique correspondante.
  2. Qu'est-ce qu'un couple oxydant/réducteur ? Citer un exemple. Écrire la demi-équation correspondante
  3. Trois solutions ioniques, de concentration c = 1,0 10 -3 mol.L-1, sont disposées dans trois flacons numérotés 1, 2 et 3, à la température de 25 °C. On dispose également de trois étiquettes, sur lesquelles sont inscrites les indications suivantes : (Na+ ; Cl- ) ; (K+ ; Cl- ) et ( Na+ ; HO- ). On désire retrouver par des mesures de conductance à quel flacon correspond chaque étiquette. La cellule est formée d'électrodes planes et parallèles, de surface 4,00 cm2, séparées d'une distance de 12,5 mm.On obtient les mesures suivantes (les électrodes sont totalement immergées) :
    flacon
    1
    2
    3
    G(µS)
    795,8
    404,5
    479,4
    - Exprimer la conductance G en fonction de la conductivité s et des paramètres géométriques de la cellule. A partir des conductances mesurées, déterminer la conductivité s des solutions 1, 2 et 3.
    - A partir des conductivités molaires ioniques, déterminer la conductivité s des trois solutions aqueuses.
    - Indiquer pour chaque flacon, l'étiquette qui lui correspond.

Données : Conductivités molaires ioniques l en S.m2.mol-1 à 25 °C :

Na+
K+
Cl-
HO-
l en S.m2.mol-1
50,1 10-4
73,510-4
76,3 10-4
198,6 10-4

corrigé
acide conjugué de l'ion borate : HBO2.

  HBO2= H+ + BO2-.

couple redox MnO4 - / Mn2+ : MnO4 - + 8 H+ + 5e- = Mn2+ + 4H2O

couple redox Fe3+ / Fe2+ : 5 Fe2+ = 5 Fe3+ + 5e-.

La forme oxydante MnO4 - du couple peut gagner des électrons et se réduire en Mn2+, forme réduite du couple.

Il y a transfert d'électrons du réducteur (Fe2+) d'un couple redox vers l'oxydant (MnO4 -) d'un autre couple redox.

constante de la cellule notée k = distance (m) / surface (m²) =12,5 10-3 / 4 10-4 = 31,25 m-1.

conductance G ( S) * constante de cellule k (m-1) = conductivité s (S m-1).

flacon
1
2
3
G(S)
7,958 10-4
4,045 10-4
4,794 10-4
conductivité s (S m-1).
7,958 10-4*31,25 = 2,49 10-2
1,26 10-2
1,5 10-2
solution de chlorure de sodium C= [Na+]=[Cl-]=1 mol m-3.

s = l Na+ [Na+] + l Cl- [Cl-] =(5,01+7,63 ) 10-3 = 1,26 10-2 S m-1 donc flacon n° 2.

solution de chlorure de potassium C= [K+]=[Cl-]=1 mol m-3.

s = l K+ [K+] + l Cl- [Cl-] =(7,35+7,63 ) 10-3 = 1,49 10-2 S m-1 donc flacon n° 3.

solution de soude ( hydroxyde de sodium) C= [Na+]=[HO-]=1 mol m-3.

s = l Na+ [Na+] + l HO- [HO-] =(5,01+19,8 ) 10-3 = 2,48 10-2 S m-1 donc flacon n° 1.

retour -menu