miroir ; dioptre plan, lame à face parallèles ; prisme
	1	miroir plan
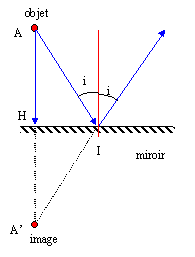
	C'est une surface plane réfléchissante. L'image formée par un miroir plan est virtuelle, située derrière le miroir ( symétrique de l'objet par rapport au plan du miroir). Cette image est inversée (gauche-droite), mais pas renversée (haut-bas). Afin de déterminer géométriquement la position d'une image, il faut tracer, à partir de l'objet, une droite normale à la surface du miroir. Le point image se trouve sur cette droite, à la même distance du miroir que le point objet correspondant. Un miroir plan est un dispositif stigmatique : à un point objet correspond un point image unique.
	2	translation d'un miroir
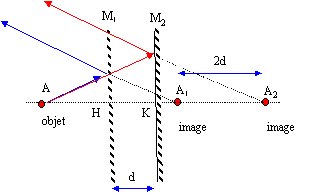
	Lorsque le miroir se déplace de d, l'image correspondante se déplace de 2d. AH= HA1 et AK= KA2. symétrie par rapport au miroir AH+d= KA1+ A1A2 ; A1A2 = AH+d- KA1avec KA1 =HA1-d= HA-d A1A2 =AH+d-(HA-d)=2d
	3	rotation d'un miroir
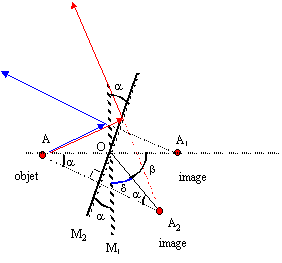
	Le miroir tourne d'un angle a, le rayon réfléchi correspondant tourne de 2a. b + d= 90 et d + 2 a= 90 : d'où : b= 2a
	4	dioptre plan ( lumière monochromatique)
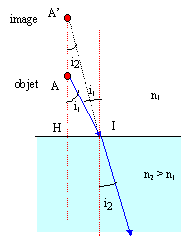
	Deux milieux transparents séparés par une surface plane. La surface plane est le dioptre plan.   tan i1 = HI/AH ; tan i2 = HI/ A'H soit AH tan i1 =A'H tan i2 n1 sin i1 = n2 sin i2 si i1 est petit, i2 est petit et on peut confondre le sinus et la tangente d'où : n1/AH= n2/A'H ( stigmatisme approché pour les rayons peu inclinés sur la normale au dioptre)
	5	lame à face parallèles
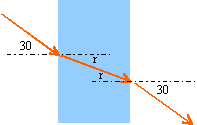
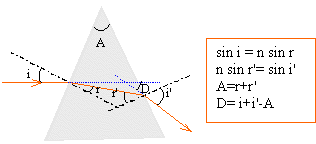
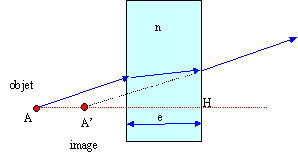
	Milieu d'indice n limité par deux plans parallèles 1 sin 30 = 1,5 sin r sin r = 0,333 d'où r = 19,47° puis dioptre verre air : angle d'incidence 19,47 ° (angle alterne interne) 1,5 sin 19,47 = 1 sin i' i' = 30° La direction du rayon émergent est indépendante de l'indice de la lame ; rayon incident et émergent sont parallèles si les milieux d'entrée et de sortie sont identiques. Le déplacement de l'image par rapport à l'objet est : AA'= e(1-1/n)
	6 le prisme Milieu transparent d'indice n limité par deux plans non parallèles. On ne peut avoir réflexion totale qu'en passant d'un milieu d 'indice n à un milieu d'indice inférieur à n. Sur la seconde face du prisme , il y a réflexion totale si l'angle r' est supérieur à l'angle limite de réfraction noté l tel que sin l = 1/n. r' inférieur ou égal à l. Les formules du prisme conduisent à : r supérieur ou égal à A-l . sin i supérieur ou égal à n sin(A-l) ce qui impose : 1 >= n sin(A-l) sin(l)>= sin(A-l) A <= 2l. La déviation D dépend de A, n et i : D = f( A,i,n). La déviation passe par un minimum Dm : au minimum de déviation le trajet du rayon lumineux est symétrique par rapport au plan bissecteur du prisme im = i' ; r = r'= ½A ; Dm = 2 im-A ; sin (½(A+Dm))= n sin (½A) D varie avec la longueur d'onde de la lumière incidente ; en effet l'indice d'un matériau varie avec l selon la Loi de Cauchy : n = P + Q/l2. 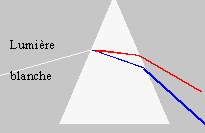7 dispersion par un prisme La dispersion d'une lumière complexe ( décomposition en lumières simples) est due à la différence des indices de la substance dispersive pour les différentes radiations. L'indice d'une substance dépend de la longueur d'onde de la lumière la traversant. n= A + B / l² Loi de Cauchy La déviation du prisme croît avec l'indice. La lumière blanche contient toutes les radiations visibles . Le violet l = 400 nm sera plus dévié que le rouge l= 750nm.     retour - menu