Aurélie dec 2004
cinétique chimique

chlorure de sulfuryle ; chlorocyclohexane ; pentaoxyde de diazote ; dismutation des ions hypochlorites

Google

A 270 °C, le chlorure de sulfuryle SO2Cl2 noté A se dissocie totalement selon l’équation bilan

SO2Cl2 (g)= S02 (g) + Cl2 (g)

Tous les constituants sont gazeux et assimilés à des gaz parfaits.

  1. Dans un récipient de volume constant, préalablement vide, on introduit du chlorure de sulfuryle et on porte le tout à 270 °C. On suit l’évolution de la réaction par mesure de la pression totale P dans le récipient, on obtient les résultats suivants.
    t (min)
    0
    50
    100
    150
    200
    250
    P (mmHg)
    306
    330
    351
    371
    390
    407
    P (Pa)
    40786
    43985
    46784
    49450
    51982
    54248
    En supposant une cinétique d’ordre 1,donner l’expression de la pression partielle PA de chlorure de sulfuryle en fonction de la pression initiale notée P0 de la constante de vitesse k et du temps t.
    - Montrer que : PA = 2 P0 - P
    - Vérifier que les résultats expérimentaux sont conformes à une cinétique d’ordre 1. Calculer la constante de vitesse k.
    - Calculer le temps de demi-réaction à 270 °C.
  2. On donne le temps de demi-réaction obtenu pour deux températures d’étude T1 = 280 °C ; t½(1) = 187,00 min. T2 = 330 °C; t½(2) = 4,21 min. En déduire l’énergie d’activation de la réaction.
  3. On admet l'intervention d'un mécanisme radicalaire :
    SO2Cl2 -->SO2Cl* + Cl* k1
    SO2Cl* -->SO2 + Cl* k2
    SO2Cl2 + Cl*--> SO2Cl* +Cl2 k3
    SO2Cl* + Cl*--> SO2 + Cl2 k4
    k1, k2, k3 , k4 sont les constantes de vitesse associées aux étapes élémentaires.
    - Etablir en appliquant l'approximation des états quasi -stationnaires aux intermédiaires SO2Cl* et Cl* , l'expression des concentrations molaires de ces espéces en fonction des constantes de vitesse k1, k2, k3 , k4 et, éventuellement, des concentrations molaires des espéces chimiques intervenant dans l'équation bilan.
    - En déduire la loi de vitesse de la réaction étudiée.

     

corrigé

v= -dPA/dt = k PA ; dPA/PA= -k dt puis intégrer

ln PA = -kt + Cte

La constante est déterminée à partir des conditions initiales : à t=0 , lnP0=Cte

ln PA = -kt + lnP0 ; ln (PA/P0 ) = -kt

SO2Cl2 (g)
= S02 (g)
+ Cl2 (g)
t=0
n = P0V/(RT) mol (3)
0
0
en cours
n-y mol
y
y
n-y = PAV/(RT) (1)

nombre total de mol à la date t : n+y = PV/(RT) (2)

additionner (1) et (2) : 2 n = (PA+P)V/(RT)

et en tenant compte de (3) : 2P0V/(RT) = (PA+P)V/(RT) ; 2P0 =PA+P ; PA= 2P0 -P.
t (min)
0
50
100
150
200
250
PA =2P0 -P (mmHg)
P0=306
282
261
241
222
205
PA /P0
1
0,92
0,85
0,79
0,72
0,67
ln(PA /P0)
0
-0,082
-0,16
-0,24
-0,32
-0,4
k = -ln(PA /P0)/t
xxxxxxxxxxx
1,63 10-3
1,59 10-3
1,59 10-3
1,6 10-3
1,6 10-3
La dernière ligne du tableau confirme l'ordre 1. k= 1,6 10-3 min-1.

à t= t½ alors PA=½P0 soit PA/P0 =0,5

or ln (PA/P0 ) = -kt, d'où : ln 0,5 = -ln 2 = -k t½.

t½ = 1/(k ln 2)=1/(1,6 10-3*ln2)=902 min.

k= cte exp(-Ea/(RT)) ou ln k = ln Cte -Ea/(RT)

ln k1 = ln Cte -Ea/(RT1) (4); ln k2 = ln Cte -Ea/(RT2) (5)

soustraire (4)-(5) : ln k1 - ln k2 = ln (k1/ k2)= Ea/R ( 1/T2-1/T1)

avec ln (k1/ k2) = ln(t½2/ t½1 ) ; Ea= R ln(t½2/ t½1 ) / ( 1/T2-1/T1)

ln(t½2/ t½1 ) = ln(4,21/187)=-3,8 ; T1 = 273+280 = 553 K ; T2 = 273 + 330 = 603 K

Ea= 2 105 J.

d[SO2Cl*]/dt = k1[SO2CL2]-k2[SO2Cl*]+ k3 [SO2CL2] [Cl*]-k4[SO2Cl*][Cl*]=0 (1)

d[Cl*]/dt =k1[SO2CL2]+k2[SO2Cl*]- k3 [SO2CL2] [Cl*]-k4[SO2Cl*][Cl*]=0 (2)

(1) + (2) donnent : 2k1[SO2CL2] =2k4 [SO2Cl*][Cl*]

soit [SO2Cl*] = k1[SO2CL2] /(k4[Cl*]) (3)

(1) - (2) donnent : 2k2[SO2Cl*]=2 k3 [SO2CL2] [Cl*]

soit [SO2Cl*] = k3 [SO2CL2] [Cl*] / k2 (4)

(3) et (4) donnent : [Cl*] ² = k1k2/(k3k4)

vitesse de la réaction : d[SO2CL2]/dt = -k1[SO2CL2]- k3 [SO2CL2] [Cl*]

puis remplacer (Cl*) par son expression ci-dessus

d[SO2CL2]/dt = -[SO2CL2]( k1 +k3 (k1k2/(k3k4))½)

Le chlorure d’hydrogène (B) réagit sur le cyclohexène (A) avec formation de chlorocyclohexane (C), selon la réaction :

C6H10 + HCl --> C6H11Cl schématisé par : A +B -->C

On réalise une série d’expériences à 25°C, où l’on mesure la vitesse initiale v0 de la réaction en fonction des concentrations molaires initiales [A]0 en cyclohexène et [B]0 en chlorure d’hydrogène dans le milieu réactionnel. Les diverses espèces sont

dans un solvant approprié et le volume réactionnel est constant et égal à 1 litre. Les résultats sont rassemblés dans le tableau ci dessous :
expérience
1
2
3
4
[A]0 mol/L
0,470
0,470
0,470
0,313
[B]0 mol/L
0,235
0,328
0,448
0,448
v0 mol s-1
15,7 10-9
30,6 10-9
57,1 10-9
38 10-9

  1. On désigne respectivement par p et q les ordres partiels initiaux de la réaction par rapport au cyclohexène A et au chlorure d’hydrogène B. Exprimer la loi de vitesse initiale de cette réaction en fonction de p et q.
  2. Déterminer p
  3. Déterminer q, puis l’ordre global de la réaction.
  4. Calculer la constante de vitesse de la réaction.
  5. On réalise dans les conditions précédentes (volume réactionnel constant de 1 litre) un mélange contenant 0,470 mol.L-1 de cyclohexène et 0,470 mol.L-1 de chlorure d’hydrogène.
  6. Si l’ordre global de la réaction est égal à 3, établir la loi de vitesse de la réaction en fonction de la concentration molaire [A] en cyclohexène à la date t, et l’intégrer.
  7. En déduire le temps de demi réaction t½ (calcul littéral puis application numérique).

 

corrigé
v= k[A]p [B]q.

expérience
1
2
3
4
[A]0 mol/L
0,470
0,470
0,470
0,313
[B]0 mol/L
0,235
0,328
0,448
0,448
v0 mol s-1
15,7 10-9
30,6 10-9
57,1 10-9
38 10-9
k= v0 / ([A]0 [B]02)

mol-1 L² s-1.
6,05 10-7
6,05 10-7
6,05 10-7
6,04 10-7
expériences 1 et 2 : [A]0 constant

[B]0 est multipliée par 0,328/0,235 = 1,4 ( proche de racine carrée de deux) ;or la vitesse v0 double: en conséquence q=2

expériences 2 et 3 : [A]0 constant

[B]0 est multipliée par 0,448/0,328 = 1,36 ( remarque : 1,36 ²=1,86) ; or la vitesse v0 est multipliée par 1,86 : en conséquence q=2.

expériences 3 et 4 : [B]0 constant

[A]0 est multipliée 0,313/0,47 = 0,66 et la vitesse v0 est aussi multipliée par 0,66 : en conséquence p=1

ordre global p+q=3

dx/dt = k(a-x)3 avec a = 0,47mol/L et x avancement en mol.

dx/(a-x)3 = kdt

intégrer : une primitive de 1/(a-x)3 est 2/(a-x)² + constante

2/(a-x)² =kt + cte

à t=0 , x=0 et cte = 2/a²

2/(a-x)² -2/a²=kt

à t½ alors x = 0,5 a

8/a²-2/a²=k t½.

t½.= 6/(ka²)=6/(6,05 10-7 *0,47²)= 4,5 107 s. 

Le pentaoxyde de diazote N2O5 gazeux se transforme par chauffage dans un récipient de volume constant en dioxyde d'azote NO2 et dioxygène O2.

  1. Montrer que les valeurs expérimentales suivantes exprimant la pression de N2O5 en fonction du temps à 45 °C sont compatibles avec une cinétique du premier ordre en N2O5. Calculer numériquement la constante de vitesse k.
    t (min)
    0
    10
    20
    40
    60
    80
    100
    120
    p(mmHg)
    348
    247
    185
    105
    58
    33
    18
    10
  2. Le mécanisme de cette réaction semble correspondre aux étapes suivantes:
    N2O5 = NO2 +NO3 k1, k2
    NO2+NO3 -> NO2+NO +O2 k3
    NO + N2O5 -> 3 NO2 k4
    Montrer que ce mécanisme est compatible avec la loi de vitesse expérimentale et proposer une relation liant k à k1, k2 et k3. On admet que les espèces NO et NO3 sont des intermédiaires réactionnels.
  3. Un argument expérimental en faveur du mécanisme postulé ci-dessus a consisté à chauffer un mélange de N2O5 et de dioxyde d'azote marqué 15 NO2. Essayer de justifier cette technique.
corrigé
cinétique d'ordre 1 ( N2O5 est noté A): v= -dPA/dt = k PA ; dPA/PA= -k dt puis intégrer

ln PA = -kt + Cte

La constante est déterminée à partir des conditions initiales : à t=0 , lnP0=Cte

ln PA = -kt + lnP0 ; ln (PA/P0 ) = -kt

t (min)
0
10
20
40
60
80
100
120
p(mmHg)
p0= 348
247
185
105
58
33
18
10
p/p0
1
0,71
0,53
0,3
0,167
0,095
0,052
0,029
-ln(p/p0)
0
0,34
0,63
1,19
1,8
2,35
2,96
3,55
k= ln(p/p0)/t
xxxx
3,4 10-2
3,16 10-2
3 10-2
3 10-2
3 10-2
3 10-2
3 10-2
à l'exception des deux premières colonnes, ces mesures confirment une cinétique d'ordre1.

k= 3 10-2 min -1.

Les intermédiaires réactionnels restent en quantité pratiquement constante et très faible.

d[Pintermédiaire] / dt =0

N2O5 = NO2 +NO3 k1, k2
NO2+NO3 -> NO2+NO +O2 k3
NO + N2O5 -> 3 NO2 k4

d PN2O5/dt = -k1PN2O5 + k2PNO2 PNO3 - k4 PNOPN2O5 (1)

d PNO/dt = 0 = k3 PNO2 PNO3- k4 PNOPN2O5

k3 PNO2 PNO3= k4 PNOPN2O5 (2)

dPNO3 /dt = 0 = k1PN2O5 - k2PNO2 PNO3- k3 PNO2 PNO3=k1PN2O5 -( k2+k3)PNO2 PNO3

k1PN2O5 =( k2+k3)PNO2 PNO3 (3)

(3) donne PNO2 PNO3 = k1/( k2+k3) PN2O5 repport dans (1)

d PN2O5/dt = -k1PN2O5 + k2k1/( k2+k3) PN2O5 - k4 PNOPN2O5 (4)

et en tenant compte de (2) et de (3) : k4 PNOPN2O5 =k3 k1/( k2+k3)PN2O5 repport dans (4)

d PN2O5/dt = -k1PN2O5 + k2k1/( k2+k3) PN2O5 - k3 k1/( k2+k3)PN2O5

d PN2O5/dt = -k1( 1-k2/( k2+k3)+ k3 /( k2+k3))PN2O5.

k= -k1( 1+ ( k3-k2)/( k2+k3)).

Le dioxyde d'azote marqué 15 NO2 apparaît dans chaque étape élémentaire et cet isotope de l'azote est stable. L' azote 15 N peut donc être utilisé comme traceur et permet de déterminer les quantités de chaque espèce.

Dans le domaine de pH où la réaction 2 Fe3+ (aq) + 2 I- (aq) -> 2 Fe2+ (aq) + I2 (aq) est totale, on se propose de décrire sa cinétique. Des résultats expérimentaux ont permis de proposer la décomposition en actes élémentaires (toutes les espèces sont en solution).

Fe3+ + I- --> FeI2+ k1

FeI2+ --> Fe3+ + I- k2

FeI2+ + I- --> Fe2+ + I2- k3

Fe3+ + I2- --> Fe2+ + I2 k4

FeI2+ et I2- sont des intermédiaires très instables et très réactifs pour lesquels on pourra faire l'approximation de l'état stationnaire.

  1. A partir de ce mécanisme, établir les expressions de d[FeI2+] / dt et de d[I2-] / dt.
  2. Établir l'expression de la vitesse globale de réaction. En supposant que l'on peut négliger k2 devant k3.[I-], simplifier l'expression obtenue précédemment. Conclure.
corrigé
d[FeI2+] / dt = k1[Fe3+][I-]-k2[FeI2+]-k3[FeI2+][I-]=0

k1[Fe3+][I-]-[FeI2+](k2+k3[I-])=0 (1).

d[I2-] / dt=k3[FeI2+][I-] - k4[I2-][Fe3+]=0 (2).

d[Fe3+]/dt = -k1[Fe3+][I-] + k2[FeI2+]- k4[I2-][Fe3+] (3)

(1) +(2)+(3)donne : d[Fe3+]/dt = - 2k4[I2-][Fe3+] (4)

(1) donne : [FeI2+]= k1[Fe3+][I-] / (k2+k3[I-])

repport dans (2) : k3k1[Fe3+][I-]2 / (k2+k3[I-])- k4[I2-][Fe3+]=0

k3k1[I-]2 / (k2+k3[I-])- k4[I2-]=0

k4[I2-]=k3k1[I-]2 / (k2+k3[I-])

repport dans (4) :d[Fe3+]/dt = - 2k3k1[Fe3+][I-]2 / (k2+k3[I-])

on peut négliger k2 devant k3[I-] : d[Fe3+]/dt = - 2k1[Fe3+][I-]

On étudie la cinétique de la formation du complexe [Co(NH3)5OH]2+

[Co(NH3)5Cl]2+ + OH- <=> [Co(NH3)4NH2Cl]+ + H2O (k1 et k-1) noté A +OH-<=> B + H2O

[Co(NH3)4NH2Cl]+ ---> [Co(NH3)4NH2]2+ + Cl- (k2) noté B -->C + Cl-

[Co(NH3)4NH2]2+ + H2O ---> [Co(NH3)5OH]2+ noté C + H2O ---> D

  1. Nommer les complexes A et D.
  2. Écrire l'équation bilan.
  3. Déterminer la vitesse de formation de [Co(NH3)5OH]2+ (noté D) en fonction des concentrations des réactifs et des constantes de vitesse données. On appliquera l'approximation de l'état quasi stationnaire aux espèces intermédiaires apparaissant dans le mécanisme: [Co(NH3)4NH2Cl]+ (noté B) et [Co(NH3)4NH2]2+ (noté C).
  4. Montrer que si k2 est petit devant k-1. [H2O], la vitesse de la réaction s'écrit :
    v = k2 k1 [A][HO-] / k-1 [H2O]

 

corrigé
[Co(NH3)5OH]2+ : pentaamminohydroxocobalt (III)

[Co(NH3)5Cl]2+ : pentaamminochlorocobalt (III)

A +OH-<=> B + H2O (k1 et k-1)

B -->C + Cl- (k2)

C + H2O ---> D (k3)

La somme des trois équations donne : A= D

d[B] / dt =k1[A][OH-] - k-1[B][H2O]-k2[B]=0

k1[A][OH-] -[B](k-1[H2O]+k2)=0 (1)

d[C]/dt = k2[B]- k3[C][H2O]=0 (2)

d[D]/dt = k3[C][H2O](3)

(2) + (3) donne : d[D]/dt =k2[B] (4)

(1) donne : [B]= k1[A][OH-] / (k-1[H2O]+k2)

repport dans (4) : d[D]/dt =k2 k1[A][OH-] / (k-1[H2O]+k2)

si k2 est petit devant k-1. [H2O] : d[D]/dt =k1 k2[A][OH-] / (k-1[H2O])

dismutation des ions hypochlorites

Partie 1: A température suffisamment élevée, les ions hypochlorite ClO- peuvent se dismuter selon la réaction totale:

ClO- --> 1/3 ClO3- + 2/3 Cl-

La vitesse de disparition des ions ClO- suit une loi cinétique de second ordre.

  1. Écrire l'équation de vitesse correspondant à la réaction. Exprimer l'évolution en fonction du temps de la concentration des ions hypochlorite dans une solution où l'on provoque cette réaction.
  2. On dispose à l'instant t = 0 d'une solution contenant des ions ClO- à la concentration de 0,1 mol.L-1.
    - Cette solution est portée à la température de 343 K pour laquelle la constante de vitesse de réaction est k = 0,0031 mol.L-1.s-1. Au bout de combien de temps aura-t-on obtenu la disparition de 30 % des ions ClO- ?
    - L'énergie d'activation de la réaction vaut 47 kJ.mol-1. Quel serait à 363 K le temps nécessaire pour obtenir un même taux d'avancement (30 %) à partir de la même solution initiale ?

Partie 2 :Méthode d'isolement d'Ostwald:

En solution alcaline, l'ion hypochlorite se dismute suivant la réaction:

3 ClO- ---> ClO3- + Cl-

On mesure la concentration de ClO- en fonction du temps dans deux solutions différentes :

1ère solution : [ClO-]0 = 1,27 .10-2 mol/L et [OH-]0 = 0,26 mol/L
t(s)
1000
3000
10000
20000
40000
100000
[ClO-] mol/L
0,0122
0,0113
0,0089
0,0069
0,0047
0,0024
2ème solution: [ClO-]0 = 2,71 .10-2 mol/L et [OH-]0 = 0,495 mol/L
t(s)
2000
10000
20000
30000
50000
100000
[ClO-] mol/L
0,023
0,0143
0,0097
0,0074
0,005
0,0027
- Quels sont les ordres de la réaction par rapport à l'ion hypochlorite et par rapport à l'ion hydroxyde ?

corrigé
équation de vitesse : d[ClO-] / dt = - k [ClO-] 2 ;

soit a la concentration initiale en ion hypochlorite ; à la date t, la concentration est a-x; soitd[ClO-] / dt = -dx/dt

dx/dt = k ( a-x)2 ; dx/ (a-x)²= k dt

intégration : 1/(a-x) = kt + constante

la constante est déterminer par les conditions initiales : 1/a = 0 + constante

1/(a-x)-1/a = kt ou 1/[ClO-]-1/[ClO-]0= kt.

La disparition de 30 % des ions ClO- est obtenu à :

1/[ClO-]0 = 1/0,1 = 10 ; [ClO-] = 0,7*0,1 = 0,03 ; 1/[ClO-] =1/0,07 = 14,28 ; k= 0,0031 mol.L-1.s-1.

t= 1/0,0031*(14,28-10)= 1380 s.

ln( k'/k)= Ea/R(1/T-1/T') = 47 103 /8,31[1/343-1/363]=0,877.

k'/k = 2,4 soit k'= 2,4*0,0031 =7,45 10-3 mol.L-1.s-1.

La disparition de 30 % des ions ClO- est obtenu à :

1/[ClO-]0 = 1/0,1 = 10 ; [ClO-] = 0,7*0,1 = 0,03 ; 1/[ClO-] =1/0,07 = 14,28 ; k= 7,45 10-3 mol.L-1.s-1.

t= 1/7,45 10-3*(14,28-10)= 574 s.

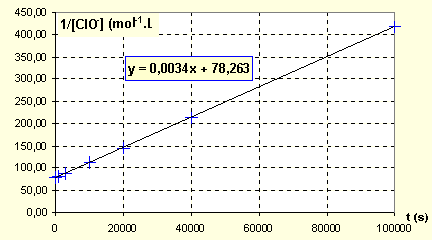
La concentration des ions hydroxyde est très supérieure à la concentration des ions hypochlorite . On peut considérer qu'à tout instant [OH-](t) = [OH-]0. Il y a dégénérescence de l'ordre par rapport aux ions hydroxydes. La loi de vitesse peut alors se mettre sous la forme :

v = kapp[ClO-]q avec kapp = k.[OH-]p

dans l'hypothèse d'un second ordre :1/ [ClO-]0 = 1/ 1,27 .10-2 = 78,7.

t(s)
1000
3000
10000
20000
40000
100000
[ClO-] mol/L
0,0122
0,0113
0,0089
0,0069
0,0047
0,0024
1/[ClO-]
82
88,5
112,3
144,9
212,8
416,7
1/[ClO-] -1/ [ClO-]0
3,3
9,8
33,6
66,2
134,1
338
(1/[ClO-] -1/ [ClO-]0) /t
3,3 10-3
3,26 10-3
3,36 10-3
3,31 10-3
3,35 10-3
3,38 10-3
Les valeurs de la dernière ligne du tableau étant constante, l'hypothése est vérifiée avec

kapp= 3,3 10-3 = k [OH-]0p = 0,26p k.

même travail pour la seconde expérience :1/ [ClO-]0 = 1/ 2,71 .10-2 = 36,9.

t(s)
2000
10000
20000
30000
50000
100000
[ClO-] mol/L
0,023
0,0143
0,0097
0,0074
0,005
0,0027
1/[ClO-]
43.5
69,9
103,1
135,1
200
370,4
1/[ClO-] -1/ [ClO-]0
8,1
33
66,2
98,2
163,1
333,4
(1/[ClO-] -1/ [ClO-]0) /t
4 10-3
3,3 10-3
3,31 10-3
3,27 10-3
3,26 10-3
3,33 10-3
kapp= 3,3 10-3 = k [OH-]0p = 0,0,495 p k.

la température des deux séries de mesures étant la même, alors k est constant.

de plus kapp est le même dans les deux cas, alors que [OH-]0 a changé : donc p=0.

La concentration des ions hydroxydes n'a pas d'influence sur la vitesse de la réaction

retour - menu