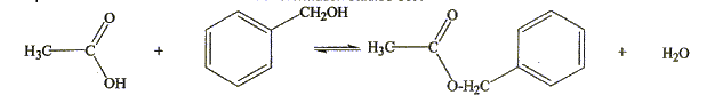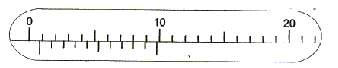|
Montages
de chimie ;
dosage
conductimétrique ; montages d'optique ; électricité
d'après concours technicien de
laboratoire 2005
|
|
|
|
|
|
Montages de chimie
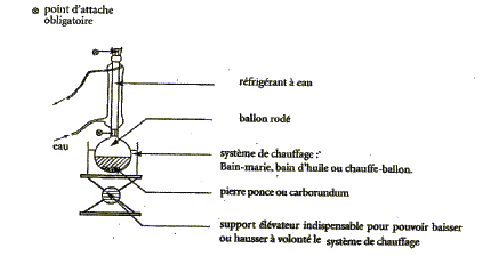
- Nommer ce montage ( chauffage à reflux)
- Quel est le rôle de la pierre ponce ? (régulariser
l'ébullition)
- Le ballon contient du
champagne, quel est l'intérêt de ce montage ? travailler à température modérée, en évitant les
pertes de matière.
- Nommer le montage ci-dessous ( distillation fractionnée)
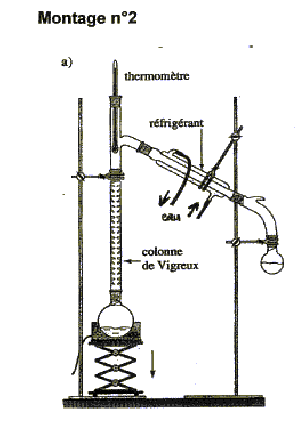
- On souhaite réaliser la synthèse du méthanoate d'éthyle.
Le ballon contient de l'acide méthanoïque, de l'éthanol dans les
proportions stoéchiomètriques et quelques gouttes d'acide sulfurique
concentré. Les températures d'ébullition sous 1 bar sont données
ci-dessous.
|
acide méthanoïque
|
100,7°C
|
|
éthanol
|
78,5°C
|
|
eau
|
100°C
|
|
méthanoate d'éthyle
|
54,3°C
|
Ecrire l'équation de la réaction de synthèse du méthanoate d'éthyle ;
nommer cette réaction
HCOOH + C2H5OH =
HCOOC2H5 + H2O estérification
- La transformation associée à
cette réaction est-elle totale ? non,
limitée par l'hydrolyse de l'ester
- Quel est le rôle de l'acide
sulfurique ? catalyseur.
- Expliquer comment procéder
pour récupérer le méthanoate d'éthyle ce
produit est le plus volatil ; il distille à 54,3°C.
- Quel est l'intérêt de ce montage ? ce
montage permet d'éliminer l'ester au fur et à mesure qu'il se forme et
de déplacer l'équilibre vers la formation de l'ester ; par ce procédé,
la réaction devient totale.
- Nommer ce montage synthèse + distillation simple
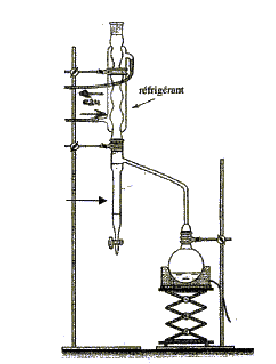
- On souhaite réaliser la synthèse
de l'éthanoate de benzile. On introduit dans le ballon nacide
= 0,1 mol d'acide éthanoïque glacial ; nalcool = 0,1 mol
d'alcool benzylique ; 5 mL de cyclohexane ; quelques cristaux d'acide
paratoluène sulfonique ; quelques grains de pierre ponce. Le tube
récepteur T est préalablement rempli de cyclohexane. L'équation de la
réaction associée à la transformation étudiée est :
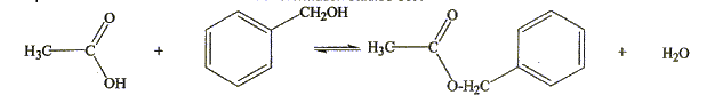
- Quel est le rôle de l'acide
paratoluène sulfonique ? ( catalyseur)
- Le flacon d'acide éthanoïque glacial porte les indications suivantes :
Expliquer comment procéder pour
prélever
Expliquer comment procéder pour
prélever 0,10 mol d'acide éthanoïque liquide
corrosif, donc port de blouse, gants et lunnette ; travailler sous
hotte ( S23) ; inflammable ( travail loin de toute flammes)
- masse d'acide à prélever : 0,1*60,05 = 6,0 g ; volume correspondant :
6 / 1,05 = 5,7 mL
prélever ce volume à l'aide d'une pipette graduée + pipeteur.
- Le mélange eau-cyclohexane est
un mélange hétéroazéotropique. L'eau et le cyclohexane ne sont pas
miscibles. Comparer sa température d'ébullition à celle de l'eau pure
et du cyclohexane.
hétéroazéotrope (c’est à dire un
mélange "intime" eau-cyclohexane qui a une température d’ébullition
différente de 100°C ou de 81°C. On obtient alors un distillat
biphasique (c’est à dire avec 2 phases). Il n’y a plus alors qu’a
séparer les 2 phases L’avantage principal de cette méthode par rapport
à une distillation "classique" tient aux températures utilisées :
l’hétéroazéotrope est distillé à des températures toujours inférieures
à 81 °C, alors que les températures d’ébullition de nombreux composés
organiques sont nettement supérieures à cette valeur. Ceci explique que
cette technique est très largement utilisée en parfumerie, où les
molécules odorantes sont souvent fragiles et ne peuvent supporter des
températures importantes.
On donne dans le tableau
ci-dessous les températures d'ébullition sous 1 bar . Que va-ton
recuillir dans le tube T. azéotrope
|
acide éthanoïque
|
118 °C
|
|
alcool benzylique
|
205°C
|
|
eau
|
100°C
|
|
éthanoate de benzyle
|
213°C
|
|
cyclohexane
|
81°C
|
Pourquoi le tube T est-il muni d'un robinet ? le volume de ce tube étant limité, il faut pouvoir en
extraire le contenu
Quel est l'intérêt du montage ? éliminer l'un des produits au fur et à mesure qu'il
se forme
Que récupère t-on dans le ballon
en fin d'expérience ? le produit le moins
volatil, dans ce cas l'ester, l'éthanoate de benzyle
|
|
dosage conductimétrique :
On souhaite doser une solution d'ammoniac, S0 de
concentration molaire volumique CNH3 voisine de 0,6 mol/L
par une solution d'acide chlorhydrique S, à la concentration exacte Cacide
= 0,100 mol/L
- L'acide chlorhydrique est un acide fort dans l'eau.
Préciser les espèces présentes dans la solution d'acide chlorhydrique
et déterminer leurs concentrations volumiques.
- Ecrire l'équation de la réaction de dosage.
- On prépare 100 mL d'une solution diluée S1
d'ammoniac de concentration voisine de 0,12 mol/L à partir de la
solution S0. Détailler le mode opératoire.
- Déterminer en mL le volume à prélever de sorte que le
volume équivalent d'acide versé soit compris entre 10 et 20 mL.
- Dans un bécher de 300 mL on introduit v1 mL de la solution
d'ammoniac, 200 mL d'eau déminarélisée, une sonde conductimétrique
reliée au conductimètre. On titre alors par l'acide et on trace
l'évolution de la conductivité s du mélange
au cours du dosage.
- Pourquoi ajoute-on de l'eau ?
- Qu'est ce qu'un conductimètre ?
- Relier les paramètres de la cellule conductimétrique à la
conductivité s de la solution et à la
conductance G de la solution. En déduire l'unité de s.
Est-il nécessaire d'étalonner le conductimètre ?
|
espèce
|
H3O+
|
HO-
|
Cl-
|
NH4+
|
|
104l0
( Sm²mol-1)
|
350
|
199
|
76,6
|
43,5
|
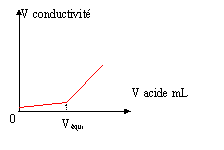
En justifiant qualitativement, dessiner l'allure de la courbe du dosage.
corrigé
Acide chlorhydrique
entièrement dissocié en ion chlorure Cl- et ion oxonium H3O+
tels que [Cl-]=[H3O+]= 0,1 mol/L
NH3 + H3O+ = NH4+
+ H2O
facteur de dilution = concentration mère / concentration fille
= 0,6 / 0,12 = 5
Prélever 20 mL de solution mère à la pipette jaugée + pipeteur
placer dans une fiole jaugée de 100 mL et compléter avec de
l'eau distillée jusqu'au trait de jauge; agiter pour rendre homogène.
Pour un volume équivalent d'acide voisin de 15 mL, la quantité
de matière d'acide, à l'équivalence est 0,1*15 = 1,5 mmol
Qté de matière d'ammoniac : 1,5 mmol ; volume d'ammoniac : 1,5
/ 0,12 = 12,5 mL
on ajoute de l'eau
afin que l'extrémité de la sonde soit correctement immergée : on mesure
la conductivité de la portion de solution comprise dans la lucarne de
la sonde. De plus, l’eau est ajoutée pour diminuer la concentration de
la solution. Les dosages conductimétriques se font à faible
concentration.
Un conductimètre mesure la conductance, ou la conductivité
d'une portion de solution électrolytique.
conductance G ( siemens) = constante de la cellule ( surface
m²/ distance m) * conductivité s ( S m-1).
il n'est pas nécessaire d'étalonner le conductimètre car le
volume équivalent est repérer lors de la rupture de pente sur le graphe.
avant équivalence
: ( NH3 en excès) la solution d'ammoniac est peu ionisée, s initiale est faible ; en ajoutant l'acide les
ions oxonium sont consommés et on obtient une solution de chlorure
d'ammonium ; la concentration [NH4+] augmente,
donc la conductivité augmente.
après équivalence : (H3O+ en
excès) la conductivité molaire ionique des ions oxonium est bien
supérieure à celle des autres ions prèsents, en conséquence la
conductivité va croître rapidement
|
|
montages d'optique
:
- Quelques questions sur les lentilles
:
- Comment au toucher distinguer une lentille convergente d'une lentille
divergent ?
- Quelle autre méthode permet de faire cette distinction ?
- Une lentille plan convexe est-elle divergente ou convergente ?
- On veut déterminer rapidement la distance focale d'une lentille
convergente. Proposer une méthode.
- On veut déterminer de manière précise la distance focale d'une
lentille convergente. On dispose d'une source lumineuse, d'un objet (
lettre p vue depuis la lanterne), d'une lentille et d'un écran.
. Obtient-on toujours une image sur l'écran ? Sinon quelle condition
doit remplir la distance entre la position de l'objet et l'écran pour
obtenir cette image ?
. On relève les mesures algèbriques suivantes de la position de l'objet
(p) et de l'image (p') par rapport au centre optique de la lentille
|
p(cm)
|
-180
|
-120
|
-100
|
-70
|
-50
|
-40
|
-30
|
-20
|
|
p' (cm)
|
20
|
21
|
22
|
24
|
28
|
33
|
45
|
180
|
Déduire de ces valeurs la vergence de la lentille
. Que remarque-t-on en regardant la première et la dernière mesure.
. Dans quel cas l'image est-elle la plus grande ? Que vaut alors le
grandissement
- Qu'est ce que la méthode d'autocollimation ?
- Comment déterminer la vergence d'une lentille divergente ?
- Pourquoi diaphragme t-on les lentilles ?
- Décrire les différents éléments d'un rétroprojecteur en précisant
leur fonction. On veut, en cours de fonctionnement, agrandir l'image
projetée sur l'écran, pour cela :
. Doit-on avancer ou reculer le rétroprojecteur par rapport à l'écran ?
. Doit-on éloigner ou approcher du document la partie
mobile du rétroprojecteur ?
Visualisation
d'objet à l'infini :
- Simulation de la lunette astronomique à l'aide de
lentilles. L'objet étant en principe très éloigné, on le considère
comme étant situé à l'infini.
- Comment simuler un objet à l'infini ? Vaut-il mieux prendre une
lentille de faible ou de forte vergence ?
La lunette est constitué de deux lentilles convergentes, la première
constitue l'objectif et la seconde l'oculaire. On veut un système
afocal c'est à dire observer l'image finale à l'infini ( oeil au repos)
. Quelle condition doivent remplir les positions des deux lentilles
pour cela ?
. On dispose d'une lentille de vergence 3d
et une autre de vergence 12 d. Attribuer
chaque lentille à l'objectif et à l'oculaire. Quel serait le
grossissement de cette lunette ? L'image obtenue est-elle droite ou
renversée ? Comment l'observer ?
- Simulation de l'oeil : comment simuler un "oeil
réduit" ?
- Simulation d'un télescope de Newton : Quel matériel
faut-il utiliser pour simuler un télescope de Newton ?
- Donner le schéma général du montage de cette simlulation.
- Interféromètre de Michelson : il est constitué,
entre autres, de deux miroirs, d'une lame séparatrice et d'une lame
compensatrice.
- Quelle propriété doit présenter une lame séparatrice ? Comment
doivent être les deux lames ?
- Avec quelle source de lumière fait-on ce réglage ? Comment vérifier
que le réglage est bon ?
- Comment doivent être les miroirs pour un bon réglage ? Que voit-on
sur l'écran lorsque le réglage est bon ?
- Par un schéma, représenter les miroirs, les lames séparatrice et
compensatrice.
corrigé
Une lentille convergente
possède des bords minces ; une lentille divergente a des bords plus
épais que sa partie centrale.
seule une lentille convergente donne
d'un objet à l'infini une image nette située dans son plan focale image.
Une lentille plan convexe ( bord mince) est convergente.
On veut déterminer rapidement la distance focale d'une
lentille convergente : former l'image d'un objet lointain ( néon allumé
par exemple) sur une feuille placée sur le sol. La distance lentille -
sol donne la distance foacle image.
Pour obtenir une image sur l'écran, la distance objet-lentille
doit être supérieure à la distance focale image ( sinon la lentille
fonctionne en loupe)
|
p(m)
|
-1,80
|
-1,20
|
-1,00
|
-0,70
|
-0,50
|
-0,40
|
-0,30
|
-0,20
|
|
p' (m)
|
0, 20
|
0, 21
|
0, 22
|
0, 24
|
0, 28
|
0, 33
|
0, 45
|
1,80
|
|
1/p
|
-0,555
|
-0,833
|
-1
|
-1,43
|
-2
|
-2,5
|
-3,33
|
-5
|
|
1/p'
|
5
|
4,76
|
4,54
|
4,16
|
3,57
|
3
|
2,22
|
0,555
|
|
1/p'-1/p
|
5,55
|
5,59
|
5,54
|
5,59
|
5,57
|
5,5
|
5,55
|
5,555
|
vergence : v= 5,55 dioptries.
la première la dernière mesure sont identiques en permuttant p
et p' : retour inverse de la lumière.
grandissement g = p'/p , d'autant
plus grand que p' est plus grand et p plus petit
g max= p'/p= 1,8 /
(-0,2) = -9 ; le signe moins signifie que l'image est inversée par
rapport à l'objet
la méthode d'auto-collimation : placer un miroir
vertical derière la lentille et chercher à obtenir une image située
dans le même plan que l'objet ; la distance lentille objet est alors
égale à la distance focale.
déterminer la vergence d'une lentille divergente : accoler une
lentille mince divergente et une lentille mince assez convergente
puis déterminer la vergence de l'ensemble. v1+v2
= vensemble.
On diaphragme les lentilles afin d'éliminer les rayons trop inclinés
sur l'axe optique principal ; on se place dans les conditions de Gauss
permettant d'obtenir des images nettes.
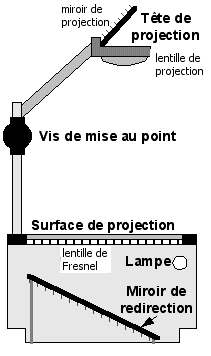
Pour agrandir l'image projetée sur l'écran :
. Reculer le rétroprojecteur par rapport à l'écran.
.Si l'objet se rapproche de la lentille (tout en restant hors
de OF : foyer objet), la distance lentille-image et le grandissement
augmente.
Un objet peut-ête considéré
comme à l'infini si la distance lentille objet est égale à 20 fois la
distance focale de la lentille. En prenant une lentille de forte
vergence ( par exemple 50 dioptries; distance focale 0,02 m) un objet
situé 40 cm devant la lentille peut-être considéré à l'infini.
Dans un système afocal, le foyer principal image de l'objectif
est confondu avec le foyer principal objet de l'oculaire.
objectif : 3d ; oculaire 12 d
Le grossissement d'une lunette afocale est égale au rapport de
la distance focale de l'objectif et de la distance focale de
l'oculaire. G= f'1 / f'2 = 12/3 = 4
L'image obtenue est inversée : une lunette astronomique donne
une image virtuelle inversée par rapport à l'objet, ce qui est sans
conséquence lorsqu'on observe un objet céleste.
L'œil doit être situé sur le cercle oculaire, cercle situé au
voisinage du foyer image de l'oculaire.
Simulation de l'oeil : L'oeil au repos peut être
modélisé par un oeil réduit. Il s'agit d'un système optique simple
constitué d'une lentille convergente et d'un écran sphérique ( la
rétine ).
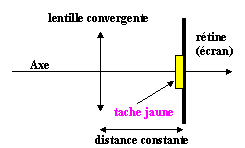
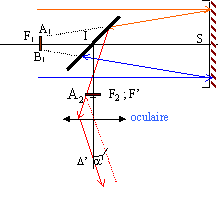
Simulation d'un télescope de Newton :
Le matériel : Un miroir sphérique concave, utilisé comme
"miroir de beauté". La distance focale de celui employé est de 40 cm.
Un fragment de miroir plan ; une lentille de distance focale 5 cm ; un
banc d'optique
-
Interféromètre de Michelson :
La lame séparatrice dont l'une des faces est légèrement
métallisée pour devenir semi-réfléchissante est placée parallèlement au
plan bissecteur de deux miroirs. Un rayon incident issu de la source
étendue S est partiellement réfléchi vers le miroir 2 et partiellement
transmis vers le miroir 1.
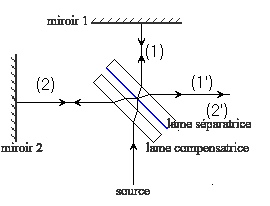
Le trajet du rayon (1) comporte trois traversées du verre de
la séparatrice et une seule pour le trajet (2). Pour rétablir l'égalité
des chemins optiques dans le verre quelle que soit l'incidence et les
longueurs d'onde des radiations utilisées, on place sur le trajet (2)
parallèlement à la séparatrice, une lame compensatrice C identique à la
séparatrice.
Source de lumière monochromatique ( laser)
Les miroirs doivent être perpendiculaires pour un bon réglage.
|
|
électricité
but : déterminer les caractèristiques de quelques
bobines
- Détermination du courant admissible dans la bobine : On
mesure la section du fil utilisé pour le bobinage à l'aide d'un pied à
coulisse. On donne ci-dessous un agrandissement du vernier.
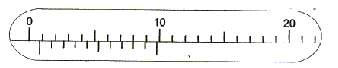
- Quel est le diamètre du fil ?
- Quelle est sa section ?
- Estimer l'intensité du courant que peut supporter ce bobinage.
- Détermination des paramètre R et L de la bobine : On
étudie la réponse à un échelon de tension d'un circuit R-L. e(t) est
une tension qui vaut 0 pour t<0 et e(t) = E pout t>=0
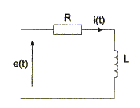
- Etablir l'équation différentielle qui lie i(t) à R, L et
E.
- Résoudre cette équation.
- En tenant compte des conditions initiales montrer que : i(t) =
E/R(1-exp(-t/t)) avect =
L/R
- Tracer l'allure de cette courbe.
- Réalisation pratique :
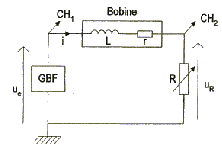
Le générateur basse fréquence est utilisé en signal carré variant entre
-5 V et 5 V, ces valeurs étant réglées à vide. sa fréquence a été
choisie suffisamment petite pour que le régime transitoire soit
entierement fini à la fin de chaque demi-période. On visualise ue
et uR sur les deux voies d'un oscilloscope.
- Pour quelle valeur de R obtient-on : uR(½T) = 0,5 ue(½T)
- Comment peut-on utiliser les calibres de l'oscilloscope pour obtenir
avec précision le rapport ½ ?
- On enregistre sur la voie 2 le signal uR pour deux
réglages différents de la base de temps.
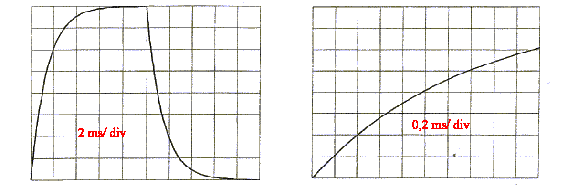
. Quelle est la fréquence du GBF ?
. Déterminer la constante de temps
. Comment l'impédance interne du GBF influe-t-il sur la mesure de la
constante de temps ?
. En déduire la valeur de l'inductance L de la bobine sachant que R= 11
W, r= 11 W
et que la résistance interne du GBF est 50 W.
- Etude du domaine de fréquence d'utilisation de cette
bobine :
On désire étudier l'évolution des paramètres r et L de la bobine en
fonction de la fréquence d'utilisation. Pour cela on utilise le montage
suivant où le générateur délivre une tension sinusoïdale de fréquance
variable.
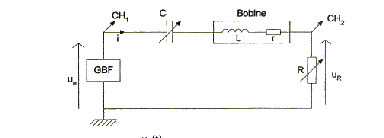
- Montrer que l'on obtient uR(t) = ½ue(t)
lorsque LCw²=1 et R = r.
- On réalise la manipulation pour différentes fréquences et on obtient
les résultats suivants :
|
f(Hz)
|
100
|
200
|
500
|
1000
|
2000
|
5000
|
10000
|
|
R ohm
|
11
|
11
|
14
|
23
|
47
|
207
|
810
|
|
C( nF)
|
25000
|
6300
|
1000
|
250
|
64
|
10
|
2,5
|
Justifier la variation de R et donc de r avec la fréquence.
- Pour les différentes fréquences calculer la valeur de L. Conclusion.
- Calculer et tracer l'évolution du facteur de qualité de la bobine Q=Lw/R en fonction de la fréquence.
- Conclure en donnant le domaine de fréquences dans lequel le
fonctionnement de la bobine est correct.
corrigé
diamètre du fil : 0,8
mm
section 3,14 d²/4 = 3,14*0,8²/4 = 0,5 mm²
l'intensité que peut supporter ce fil est de l'ordre de
l'ampère. Un fil de section 1,5 mm² peut supporter 10 A
La résistance électrique est proportionnelle à l'inverse de la
section ; l'effet Joule est proportionnel à la résistance électrique.
e(t) = Ri + Ldi/dt :
pour t >=0 E= Ri + Ldi/dt
solution particulière de cette équation : i= E/R ( en régime
permanent)
solution générale de Ri + Ldi/dt =0 : i (t)= A exp (-t/t) avect = L/R
solution générale de l'équation différentielle : i (t)= A exp
(-t/t) + E/R
à t=0 l'intensité est nulle d'où : 0=A+E/R soit A= -E/R
i(t) = E/R(1-exp(-t/t))
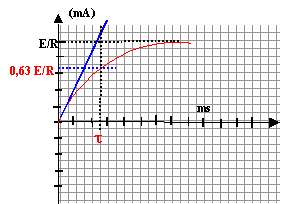
A la fin de chaque
demi période le régime permanent est établit et la bobine se comporte
comme une résistance de valeur r ; si r=R on obtient : uR(½T)
= ubobine(½T) = 0,5 ue(½T)
Comment peut-on utiliser les calibres de l'oscilloscope pour
obtenir avec précision le rapport ½ ? par exemple 1 V/div sur la voie 1
et 0,5 V/div sur la voie 2 : les deux courbes sont identiques.
fréquence du GBF
: une période correspond à 10 div soit 2*10 = 20 ms = 0,02 s ; la
fréquence est l'inverse de la période exprimée en seconde : f= 1/0,02 =
50 Hz.
constante de temps : à t= t
l'intensité est égale à 63% de sa valeur maximale ; donc à t=t, uR= 63% de sa valeur maxi
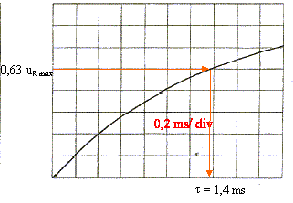
Comment l'impédance interne du GBF influe-t-il sur la mesure de la
constante de temps : la constante de temps est égale à l'inductance
divisée par la somme des résistance du dipôle RL
t = L/SR=
1,4 10-3 s
L= 1,4 10-3 (11+11+50)=0,1 H.
impédance du dipole
RLC : Z=[(R+r)² + (Lw-1/(Cw)²]½
;
à la résonance d'intensité, Lw-1/(Cw)= 0 et l'impédance est minimale, égale à Zmini
= R+r. Les effets de la bobine neutralisent ceux du condensateur. uR+uL=
(R+r) I0 = ue(t)
si R= r alors uR= uL=½ ue(t)
En très hautes fréquences (dès 100MHz) l'espacement d'une
spire à l'autre présente une capacité parasite qui peut prendre des
proportions importantes par rapport à l'effet inductif recherché. Le
comportement de la bobine peut se représenter par une bobine idéale en
parallèle avec un condensateur idéal pour les effets réactifs.
Le schéma est complété par une résistance parallèle Ra
qui traduit les pertes du circuit magnétique et par une résistance
série Rc qui traduit la résistance du fil électrique enroulé.
A fréquence non nulle une partie de la section des conducteurs
n'est pas utilisée, les lignes de courant se rejettent mutuellement
vers la périphérie, cela augmente la résistance. Lorque la fréquence
augmente l'effet de peau modifie la répartition du courant dans le
conducteur ohmique, modifiant par la même la résistance de ce
conducteur.
|
f(Hz)
|
100
|
200
|
500
|
1000
|
2000
|
5000
|
10000
|
|
w = 2 p f (rad/s)
|
628
|
1256
|
3140
|
6280
|
12560
|
31400
|
6,28 104
|
|
C(F)
|
2,5 10-5
|
6,3 10-6
|
10-6
|
2,5 10-7
|
6,4 10-8
|
10-8
|
2,5 10-9
|
|
w ²
|
3,94 105
|
1,58 106
|
9,86 106
|
3,94 107
|
1,58 108
|
9,86 108
|
3,94 109
|
|
L= 1/(Cw ²) (H)
|
0,101
|
0,1
|
0,101
|
0,1015
|
0,1011
|
0,1014
|
0,1015
|
L est constante dans ce domaine de fréquence
|
w (rad/s)
|
628
|
1256
|
3140
|
6280
|
12560
|
31400
|
62800
|
|
Lw
|
62,8
|
125,6
|
314
|
628
|
1256
|
3140
|
6280
|
|
SR = 2R+50 (ohm)
|
72
|
72
|
78
|
96
|
144
|
464
|
1670
|
|
Q= Lw / SR
|
0,87
|
1,74
|
4,02
|
6,54
|
8,7
|
6,8
|
3,8
|
Le facteur de qualité passe par un maximum pour une fréquence proche de
2000 Hz.
largeur de la bande passante à - 3 dB : Df
= S R / (2pL) ;
S R voisin de 200 W vers 2000 Hz ; Df
voisin 200 / 0,628 voisin 320
Domaine de fréquences : 1840 - 2160 Hz
|
|
retour -menu
|