Aurelie 5/5

tige fixée à un cerceau vertical.

d'après concours kiné Nantes98




Google



tige fixée à un cerceau vertical ( 10 pts)

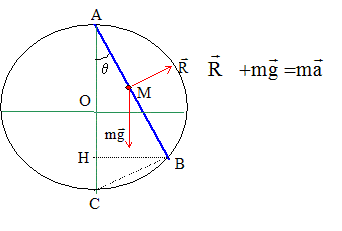
Une tige AA', fixée en A à un cerceau vertical de rayon R peut prendre toutes les orientations ( q compris entre 0 et 90°) gràce à un anneau solidaire d'un système de fixation B se déplaçant sur le cerceau. Un solide ponctuel M de masse m est lâché en A à t=0 sans vitesse et parcourt le trajet L=AB.

On done R= 1,60 m ; m= 0,1 kg et g=10 m/s².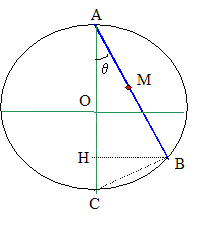

  1. On suppose les frottements négligeables. Déterminer l'accélération a0 du mouvement de M.
    - Montrer que la durée T0 du parcours AB est la même que'elle que soit l'inclinaison     q de la tige. Calculer T0.
  2. En fait il y a des frottements; le coefficient de frottement m( statique et cinétique) est constant. On rappelle que m = f/N; f est la composante de frottement et N la composante normale de la réaction R exercée par la tige sur M. La durée T du parcourt varie avec l'inclinaison, comme le montre le graphe ci-dessous. La courbe admet une asymptote verticale pour q=ql=70,7°.

    - Faire un schéma des forces en présence. - Ecrire la relation fondamentale de la dynamique; déterminer m.
    - Etablir la relation donnant T en fonction de T0,     m et q.
    - On fixe la tige à     q=60°. Calculer la valeur de T et vérifier sur le graphe.
    Avec quelle vitesse le mobile M arrive-t-il en B ?
    Calculer le travail de la force de frottement.

 

corrigé

systéme étudié : le point M ; référentiel terrestre galiléen; axe AB, d'origine A, sens : A vers B.

La seconde loi de Newton s'écrit sur cet axe : mg cosq = ma0 soit a0=gcosq.

La vitesse est une primitive de l'accélération : v= gcosq t + v0 = gcosq t

la position est une primitive de la vitesse : x= ½gcosq t 2+ OM0 = ½gcosq t 2.

distance AB= ACcosq = 2Rcosq.

d'où : 2Rcosq = ½gcosq T02 soit T02 = 4R/g, indépendant de q.

T0= (4*1,6/10)½= 0,8 s.

 

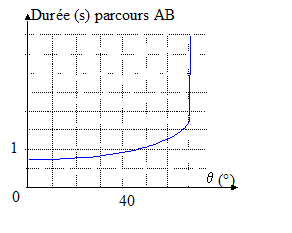
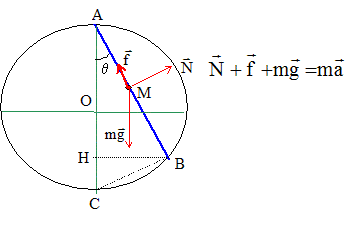
écrire la relation fondamentale de la dynamique sur l'axe AB, sens A vers B et origine A.

-f+mgcosq=ma ; a= -f/m + gcosq

écrire la relation fondamentale de la dynamique sur un axe perpendiculaire à AB : N-mgsinq=0 ;

N= mgsinq ; or f= mN =mmgsinq ; f/m = mgsinq ;

a= g(cosq - msinq )

vitesse, primitive de l'accélération : v = g(cosq - msinq ) t

position, primitive de la vitesse : x= ½g(cosq - msinq ) t²

T²= 2AB/(g(cosq - msinq )) avec AB= 2R cosq.

T²= 4Rcosq/(g(cosq - msinq ))= 4R / (g(1- m tanq) )

dériver T par rapport à q : 2T dT = -4Rm/(gcos²q(1- m tanq) 2) dq.

l'asymptote verticale correspond à 1- m tanql=0 soit m =1/ tanql = 1/ tan70,7 = 0,35.

or T02 = 4R/g d'où T²=T02 / (1- m tanq)

T= T0(1- m tanq)-½=0,8(1-0,35 tan60)-½=1,27 s.

confirmé par la lecture sur le graphe pour q=60°.

vitesse du mobile en B : v = g(cosq - msinq ) T

v= 10(cos60-0,35 sin60)*1,27 = 2,5 m/s.

travail des frottements sur le parcours AB:

variation de l'énergie cinétique : ½mv²-0

travail du poids moteur en descente : mgAH= mgABcosq= 2mgRcos²q

travail des frottements W résistant

écrire le théorème de l'énergie cinétique entre A et B

½mv²= mgABcosq + W soit W= ½mv²-2 mgRcos²q

W= 0,05*2,5² - 2*1,6*cos²60 =0,31-0,8 = -0,49 J.



retour -menu