|
spectroscopie ; butanol ; acide monochloroéthanoïque ; dibrome d'après concours kiné Nantes 2005 |
|||||||||||||||||
|
|
|||||||||||||||||
|
|||||||||||||||||
|
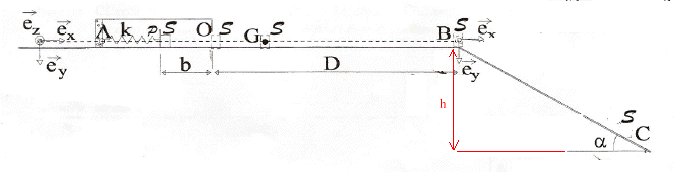
corrigé Les vecteurs sont éctits en bleu et en gras. Le solide est soumis à son poids, à l'action du support et à la tension F = -kx ex du ressort. En absence de frotement le poids et l'action du support se neutralisent. Suivant l'axe (O ex ) la seconde loi de Newton s'écrit : -kx= mx" soit x" + k/m x=0 ; on pose w²= k/m = 250/0,1 = 2500 ; w = 50 rad/s. x" +w² x=0 ; période T0 = 2p / w = 2p [m/k]½ = 2*3,14 [0,1 / 250 ]½ = 0,126 s. x(t) = -b cos( 2pt/T0 ) ; dériver par rapport au temps : vitesse v(t) = x'= b 2p /T0 sin( 2pt/T0 ) dériver une seconde fois : x" = b [2p /T0 ]² cos( 2pt/T0 ) = b w² cos( 2pt/T0 ) repport dans l'équation différentielle : b w² cos( 2pt/T0 ) + w² (-b) cos( 2pt/T0 ) = 0 est bien vérifiée quel que soit t. force de rappel, colinéaire à (x ex ) mais de sens contraire F (t) = -k x ex : F (t) = k b cos( 2pt/T0 ) ex = 250*0,1 cos (50 t)ex = 25 cos (50 t)ex. énergie potentielle élastique stockée initialement par le ressort comprimé: ½kb² énergie mécanique initiale du système{ ressort + solide S} : ½kb² + ½mv² = ½kb² Au passage à la position d'équilibre, au point O, l'énergie potentielle élastique est nulle, l'énergie cinétique est maximale : ½mV²0. En absence de frottement, l'énergie mécanique se conserve : ½kb² = ½mV²0. soit V²0 = k/mb² = 250/0,1 *0,1² = 25 et V0 = 5 m/s. Appliquer le théorème de l'énergie cinétique entre O et D : le solide est soumis à son poids, à l'action normale du support et à la force de frottement ; le poids et l'action normale du support, perpendiculaires à la vitesse, ne travaillent pas. travail résistant de la force de frottement : -mmgD variation d'énergie cinétique : ½mV²B - ½mV²0. La variation de l'énergie cinétique est égale à la somme des travaux des forces : ½mV²B - ½mV²0 = -mmgD ; V²B - V²0 = -2mgD m = (-V²B + V²0 ) / ( 2gD). le solide en chute libre n'est soumis qu'à son poids ; l'accélération de son centre d'inertie G est a= gey. vitesse initiale en B : VB=VBex. le vecteur vitesse est une primitive du vecteur accélérationa : Vx = VB ; Vy = gt le vecteur position est une primitive du vecteur vitesse : x = VB t ; y = ½gt² trajectoire : y = ½g /V²B x². au point d'impact C : yC= L sin a; xC= Lcos a. V²B= ½g x²C/yC =½g L cos² a / sina = g L cos² a = 10*1,6 cos² 30 = 16 cos²30 = (4 cos 30)² soit VB= 4 cos 30 = 3,464 m/s. m = (-V²B + V²0 ) / ( 2gD) m = ( -3,464 ² + 5²) / (20) = 0,65.
|
|||||||||||||||||
|
La partie II est largement indépendante de la partie I. I. Les niveaux d'énergie, En, de l'atome d'hydrogène sont donnés par la relation En = -E0 / n², E0 est une constante positive et n un nombre entier positif. L'énergie nulle correspond à l'atome ionisé (noyau et électron très éloignés et au repos).
II
énergie mise en jeu lors de la transition du niveau p vers le niveau m : E= Ep- Em = E0 (1/ m²- 1/ p²) énergie du photon émis : E= h c/l = E0 (1/ m²- 1/ p²) 1/ l = E0
/ (hc) (1/ m²- 1/ p²) avec RH = E0
/ (hc)
1/ l = 1 / 656,3 10-9 = 1,524 106 m-1. (1/ m²- 1/ p²) = 1/4-1/9= 0,1389 RH = 1,524 106 / 0,1389 = 1,097 107m-1. E0 = 1,097 107 * (6,62 10-34*3 108) =2,18 10-18 J 2,18 10-18
/ 1,6 10-19 = 13,6 eV.
longueurs d'onde des radiations Hb(p =4), Hg (p = 5) et Hd(p = 6) 1/l b = 1,097 107 (1/2²-1/4²) soit l b = 486,2 nm ( bleu ) 1/l g = 1,097 107 (1/2²-1/5²) soit l b = 434 nm ( bleu violet) 1/l d = 1,097 107 (1/2²-1/6²) soit l b = 410,2 nm ( violet) .
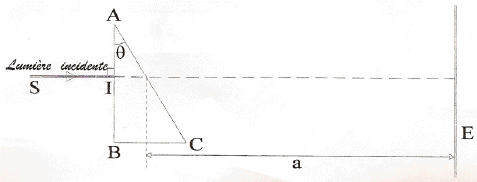
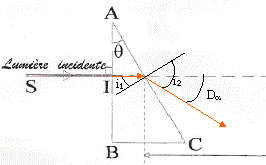
loi de Descartes pour la réfraction : Na sin i1 = sin i2 avec i1 = q = 30° Da = i2 - i1 soit i2 = Da + i1 = 62,8° ; Na = sin i2 / sin i1 = 1,7788. vitesse de propagation des ondes dans le milieu transparent d'indice Na : Va = c/Na = 3 108 / 1,7788 = 1,686 108 m/s. Le prisme est un milieu dispersif, donc on observe 4 raies sur l'écran, le violet étant le plus dévié, le vert le moins dévié.
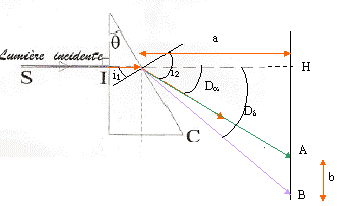
b= AB = HB-HA= a (tan Dd-tan Da) tan Dd=tan Da + b/a = tan 32,8 + 0,0542/0,5 = 0,7528 soit Dd=36,97°. puis la loi de Descartes pour la réfraction donne Nd=sin( Dd+ 30)/ sin 30 = 1,840. loi de Cauchy : N =K1+ K2/l² Na =K1+ K2/l²a et Nd =K1+ K2/l²d soit Nd - Na = K2(1/l²d-1/l²a) = K2(5,943-2,321) 1012. K2 =(1,84-1,7788) /3,622 1012 soit K2 =1,69 10-14 m-2. Na
=K1+ K2/l²a donne K1=Na- K2/l²a = 1,7788
-1,69 10-14 /(6,563 10-7)²=
1,74.
|
|||||||||||||||||
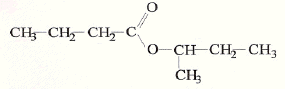
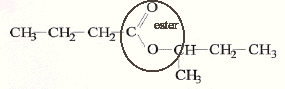
corrigé CH3-CH2-CH2-CH2OH butan-1-ol alcool primaire donne l'acide butanoïque par oxydation ménagée ( excès d'oxydant) CH3-CH(CH3)-CH2OH 2-méthylpropan-1-ol alcool primaire CH3-CH(OH)-CH2-CH3 butan-2-ol alcool secondaire CH3-C(CH3)2-OH 2,2-diméthylpropan-2-ol alcool tertiaire butanoate de 1-méthylpropyle CH3-CH2-CH2-CO2H + CH3-CH(OH)-CH2-CH3 = CH3-CH2-CH2-CO2-CH(CH3)-CH2-CH3 + H2O acide butanoïque + butan-2-ol = butanoate de 1-méthylpropyle + eau
|
|||||||||||||||||
|
Un volume Va = 10 mL d'une solution A d'acide monochloroéthanoique est dosé, en présence de phénolphtaléine ( zone de virage [8,2 ; 10]), par une solution B de soude de concentration Cb= 0,080 mol/L. A l'équivalence le volume de solution B versé est Vb= 12,5 mL. On note S la solution obtenue à l'équivalence et V son volume total.
corrigé ClCH2-COOH + HO- = ClCH2-COO- + H2O à l'équivalence les quantités de matière des réactifs sont en proportions stoéchiométriques Ca Va = Cb Vb soit Ca = Cb Vb / Va = 0,08*12,5 / 10 = 0,1 mol/L. a = [A-]éq / ([AH]éq + [A-]éq) = [A-]éq / C. conservation de A : [AH]éq + [A-]éq = CaVa/ V = C 1 - a = 1- [A-]éq / C = (C- [A-]éq )/ C =[AH]éq / C. pH = pKa + log ([A-]éq /[AH]éq ) pH = pKa + log (a / (1 - a)) si Ka = 1,8 10-4 alors pKa = -log(1,8 10-4)= 3,745 ; a proche de 1 pH = 3,745 + log ( 1 / 3,53 10-5) = 8,2. l'indicateur a été bien choisi car sa zone de virage contient le pH du point équivalent.
|
|||||||||||||||||
|
A température élevée, le dibrome Br2 se dissocie partiellement pour donner du brome monoatomique Br. Le dibrome et le brome monoatomique sont des gaz. On porte 1,6 g de dibrome à la température q =1600 °C sous la pression P0=1013 hPa.
Ondonne : Constantedesgaz parfaits: R =8,314I K-1.mol-1. Masse molaire atomique de brome: M(Br) = 80 g.mol-1. corrigé Br2 (g) --> 2 Br (g) équation des gaz parfait : PV= nRT avec T= 1600+273 = 1873 K ; P= 1,013 105 Pa ; n = 1,6 / (80*2) = 10-2 mol dibrome V1= nRT/P = 10-2*8,314*1873 / 1,013 105 =1,54 10-3 m3. si tout le dibrome est dissocié en brome : n( Br) = 2 n(Br2) = 0,02 mol en conséquence le volume du brome monoatomique est : V2= 3,08 10-3 m3.
de plus n = PV/(RT) avec : V= 1,92 10-3 m3 n= 1,92 10-3 * 1,013 105 /(8,314*1873) = 1,25 10-2 mol soit xéq = 2,5 10-3 mol. coefficient de dissociation a du dibrome : xéq / n (Br2) initial = 2,5 10-3 / 10-2 = 0,25.
|
|||||||||||||||||
|
|