|
spectroscope à réseau; déviation des électrons ; bobine. |
|||
|
|
|||
|
|||
|
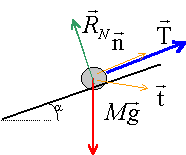
Un solide S considéré comme ponctuel de masse m= 0,690 kg se déplace sur un plan incliné faisant un angle a=20° avec le plan horizontal . Ce solide est relié à un axe placé sur le bord supérieur du plan incliné et normal à celui-ci par un fil inextensible de masse négligeable de longueur L= 0,5 m. g=9,8 m/s². Le solide est mis en mouvement depuis le point I avec une vitesse initiale v1. Au cours du mouvement le fil reste constamment tendu. Le mouvement du solide est étudié dans un repère lié à la terre et considéré comme galiléen. 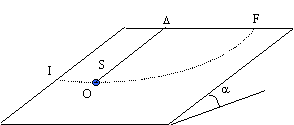
corrigé La trajectoire du solide est un arc de cercle. Le solide est soumis à son poids, vertical vers le bas, à l'action du plan , normale au plan et à la tension du fil. La somme vectorielle de ces forces est différente de zéro : d'après le principe d'inertie le mouvement n'est pas uniforme.
vecteur accélération en O : On choisit le repère de Frenet ( l'un des axes est colinéaire et de même sens que la vitesse, l'autre est confondu avec le fil et dirigé vers l'axe D) La somme vectorielle des forces est égale au produit de la masse du mobile par l'accélération de son centre d'inertie. suivant l'axe O t , la somme vectorielle des forces est nulle et en conséquence l'accélération tangentielle est nulle. suivant O n la composante normale de l'accélération vaut aN=v0²/ L = 4/0,5 = 8 m/s². De plus la seconde loi de Newton s'écrit suivant O n : m aN= T-mg sin a. d'où T=
m(v0²/L+gsin a
) = 0,690*(8+9,8 sin 20)=
7,83
N.
variation d'énergie cinétique entre O et F : DEc= ½mvF²-½mv0². l'action du plan et la tension du fil, perpendiculaire à la vitesse, ne travaillent pas. travail du poids résistant ( ça monte )de O en F : -mgL sin a. écrire le théorème de l'énergie cinétique : ½mvF²-½mv0² = -mgL sin a. vF²= v0²-2gL sin a. vF²
= 4-2*9,8*0,5*sin20 = 0,648 ;
vF= 0,805 m/s.
travail des frottements, colinéaire à la vitesse, mais de sens contraire, de valeur f constante, entre O et F : valeur de f * longueur de l'arc AB *cos180 = -f Lp/2 la différence entre l'énergie cinétique calculée et l'énergie cinétique réelle en F est égale au travail des frottements -f Lp/2 = ½mv²F réelle-½mv²F calcul. f = m(v²F calcul-v²F réelle)/(Lp)= 0,69(0,805²-0,5²)/(0,5*3,14)=0,175 N.
|
|||
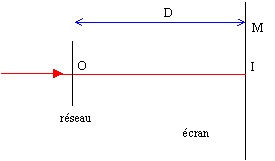
corrigé interférences constructives : les amplitudes des ondes qui interfèrent s'ajoutent ; l'amplitude résultante est maximale. Dans la région où se superposent les ondes, l'intensité lumineuse passe par des maximums et des minimums qui peuvent être nuls. Les maximums dépassent la somme des intensités des faisceaux pris séparément. La zone d'ordre p=0 se trouve en I ( d'après sin q= pl/a , si p=0 alors q =0) Un laser émet une lumière quasiment monochromatique. tan q = IM / D= 0,145 / 1,4 =0,1036 sin q =0,1036 =l/a avec a = 6,1 10-6 m l
= 0,1036 * 6,1 10-6 = 6,32 10-7 m =
632
nm.
bleue : 436 nm ; verte : 546 nm ; jaune : 577 nm ; 579 nm pour l = 577 nm : sin q=577 10-9 / 6,1 10-6 =0,0946 ; tan q = 0,0946 = IM1/ 1,4 ; IM1=0,1324 m = 132,4 mm pour l = 579 nm : sin q=579 10-9 / 6,1 10-6 =0,0949 ; tan q = 0,0949 = IM1/ 1,4 ; IM2=0,1329 m = 132,9 mm La différence
IM2-IM1 est inférieure à
1 mm : ce spectroscope ne permet pas, au premier ordre, de
voir distinctement les raies de 577 et 579 nm.
|
|||
|
Dans tout l'exercice on néglige le poids de l'électron devant les autres forces qui agissent sur lui. 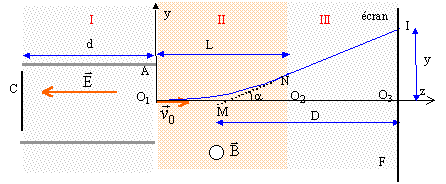
corrigé Dans la région I les électrons ne sont soumis qu'à une force électrique colinéaire au champ électrique E, mais de sens contraire ( car q négative ). La seconde loi de Newton s'écrit sur l'axe horizontale Cz : ma = eE soit a = eE/m = constante. Sous l'action de cette force il sont animés d'un mouvement rectiligne uniformément accélérés entre C et A. variation d'énergie cinétique entre C et A : DEc= ½mv0²-0 =½mv0² travail moteur de la force électrique entre C et A : eUAC = eEd. th. de l'énergie cinétique :½mv0² =eEd. soit v0²=2 e Ed / m. v0²= 2*1,6
10-19 * 5 104 *0,1/ 9,1
10-31 =1,76 1015 ; v0 =
4,19 107
m/s.
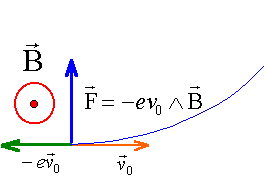
Dans la région II l'électron n'est soumis qu'à la force magnétique F , perpendiculaire à la vitesse, donc dirigée vers le centre du cercle. L'accélération est en conséquence centripète aN= v0²/R La seconde loi de Newton s'écrit, suivant l'axe n de la base de Frenet : ev0B= maN soit aN =ev0B/ m ev0B/ m =v0²/R ;eB/ m = v0/R ; R=mv0/(eB) ; R=9,1 10-31 * 4,19
107 / (1,6 10-19 * 2 10-3)=
0,12
m.
de plus tan a = O3I/D= y/D voisin de a car l'angle est petit. LeB /(mv0) = y/D ; y =LeBD /(mv0). v0 = LeBD/(my) =10-2*1,6 10-19 *2 10-3 * 0,4 / (9,1 10-31 * 0,0335)= 4,2 107 m/s. en accord avec la valeur
trouvée ci-dessus.
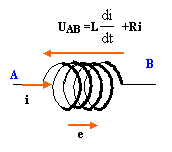
Un solénoïde de 1000 spires par mètre dont la longueur peut être considérée comme infinie est alimenté sous une tension périodique telle que l'intensité i du courant qui le traverse varie en fonction du temps comme indiqué ci-dessous. 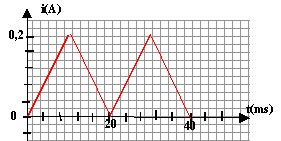
corrigé A l'intérieur du solénoïde le champ magnétique est uniforme. Sa valeur est B= m 0 nI. 
t compris entre [0 ; 10 ms] : i est une fonction linéaire de coefficient directeur 0,2 / 0,01 = 20A s-1; i(t) = 20 t. t compris entre [10 ; 20 ms] : i est une fonction affine décroissante de coefficient directeur -0,2 / 0,01 = -20A s-1; i(t) = -20 t + b ; i(t=0,01)= 0,2 =
-20*0,01 + b ; d'où b =0,4 A
. i(t) = -20 t
+0,4.
première demi-période : le champ inducteur augmente, en conséquence le champ induit est de sens contraire au champ inducteur ; le courant induit est de sens opposé à i(t).
e = -uAB = -(0,1*20+50 i(t) )= - 2- 50 i(t) = -2 -50*20t = -2 - 1000 t avec t compris entre 0 et 0,01 s. seconde demi-période : le champ inducteur diminue, en conséquence le champ induit a le même sens que le champ inducteur ; le courant induit a le sens de i(t). e = - uAB =
-(0,1*(-20)+50 i(t) )= 2- 50 i(t) = 2 -50*(-20t +0,4)= -18 +
1000 t avec t compris entre 0,01 et 0,02 s.
impédance de la bobine: Z= racine carrée ( R²+(Lw)²) = ( 50²+(0,1*314)²)½= 59 W. intensité efficace
Ieff =ueff /Z = 14,14 / 59 =
0,24
A.
|
|||
|
|