Dans le modèle dit planétaire de l'atome d'hydrogène on suppose que l'électron a un mouvement circulaire de rayon r autour du noyau constitué d'un proton. Ce mouvement a lieu sous l'action de la seule force que l'on prendra en compte, à savoir une force électrostatique attractive agissant sur l'électron dont la direction est celle de la droite joignant le proton et l'électron et dont la valeur est égale à ke²/r² où e représente la charge élémentaire et k une constante. On notera m la masse de l'électron.

1. Montrer que le mouvement de l'électron est uniforme.
2. Etablir l'expression de la vitesse en fonction de k, e, r et m.
3. On admet que l'électron soumis à la force électrostatique possède une énergie potentielle ègale à -ke²/r ; en déduire l'énergie mécanique de l'électron en fonction de k, e et r.

masse de l'électron m = 9,1 10^-31 kg ; e= 1,6 10^-19 C ; k= 9 10⁹ SI ; r= 5,3 10^-11 m.

On se propose d'étudier la chute libre d'une bille supposée ponctuelle, lachée sans vitesse initiale. On négligera les frottements et on prend g= 9,8 m/s².

1. Etablir l'équation horaire de la bille sur un axe verticale descendant avec pour origine de l'axe la position du lâcher de la bille.
2. De quelle hauteur, par rapport au sol, doit-on lâcher cette bille pour qu'elle parcourt les dix derniers cm en 40 ms ?
3. On veut déterminer expérimentalement la vitesse de la bille en fonction de sa hauteur de chute h. Pour cela on place un capteur qui déclenche une horloge électronique lorsque la bille est tombée de h-0,05 m et un second capteur qui arrête l'horloge pour une hauteur de chute de h+0,05 m. La vitesse "expérimentale" calculée pour une hauteur de chute h, est donc donnée en m/s par 0,1 / Dt où D t représente la durée en seconde affichée par l'horloge.
   - En utilisant l'équation horaire de la question 1 calculer Dt pour h= 0,8 m.
   - En déduire la vitesse expérimentale que l'on devrait mesurée.
   - Calculer l'écart avec la vitesse instantanée théorique aquise par la bille après une chute de 0,8 m.
   - L'horloge utilisée possède une précision égale à 1 ms. La durée Dt affichée peut donc varier de plus ou moins une milliseconde. Dans quel intervalle peut donc varier la vitesse expérimentale mesurée pour une hauteur h=0,8 m ?

1. On réalise un circuit série comprenant un solénoïde d'inductance L, un condensateur de capacité C, un résistor R et un interrupteur K. Après avoir chargé le condensateur, on ferme l'interrupteur et on visualise à l'oscilloscope les variations de l'intensité du courant traversant le circuit. On obtient l'oscillogramme ci-dessous :

   - Faire un schéma du circuit en indiquant les branchements de l'oscilloscope.
   - Identifier le phénomène observé et interpréter l'oscillogramme.
   - Le signal est qualifié de pseudo-périodique. Pourquoi ?
   - Déterminer la pseudo-période et la pseudo-pulsation de ce signal.
   - Déduire du résultat précédent la valeur de L si C= 5 mF.

2. On réalise un circuit série comprenant un générateur délivrant une tension alternative sinusoïdale de pulsation w, un résistor de résistance R= 150 W, le solénoÏïde d'inductance L et un condensateur de capacité C= 5 m F. On branche un oscilloscope bicourne de manière à visualiser sur la voie A la tension aux bornes du générateur ( sensibilité 1 V/div) et sur la voie B la tension u aux bornes du résistor( sensibilité 1 V/div). a vitesse de balayage correspond à 1 ms/div.
   - Donner les expressions en fonction du temps de la tension aux bornes du générateur et de l'intensité du courant.

   - Construire le diagramme de Fresnel des tensions.
   - A partir de ce diagramme déterminer la valeur de l'inductance de la bobine. Comparer à la valeur trouvée ci-dessus.

3. Donner l'expression de :
   - l'intensité efficace I traversant le circuit en fonction de la tension efficace du circuit U, de R, L, C et w.
   - l'intensité efficace I₀ traversant le circuit à la résonance.
   - Etablir l'expression y= I/I₀ en fonction de Q= Lw₀/R = 1/(RCw₀) et de x= w /w₀ si w ₀ représente la pulsation à la résonance.
   - Calculer la bande passante de ce circuit.

---

---

corrigé

---

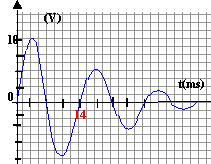
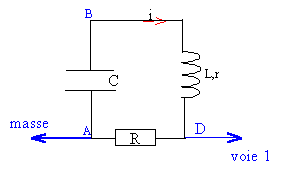
La tension aux bornes d'un résistor et l'intensité qui le travers sont proportionnelles. Visualiser la tension aux bornes du résistor c'est observer l'image de l'intensité au facteur R près.

Le signal est pseudo-périodique : l'amplitude des oscillations diminue au cours du temps : une partie de l'énergie se dissipe dans le résistor lors des échanges d'énergie entre condensateur et bobine.

Pseudo-période T = 14 ms = 0,014 s ; fréquence f = 1/0,014 = 71 Hz

pseudo-pulastion w =2pf = 6,28 *71 =448 rad/s.

LCw²= 1 d'où L=1/(Cw²) = 1/(5 10^-6 *448²)= 1 H.

---

tension aux bornes du générateur u_G=5 sin ( w t + j)

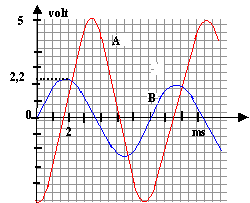
avec : T= 7 10^-3 s ; f = 1/7 10^-3 =143 Hz et w = 2pf = 897 rad/s

La phase de l'intensité est choisie comme origine des phase et la tension u_G est en avance d'environ 1,5 ms sur l'intensité.

soit 1,5/7*2p =1,35 rad donc j = 1,35 rad

expression de l'intensité : i( t) = I_max sin ( w t ) avec I_max = 2,2 / R= 2,2 / 150=0,0146 A.

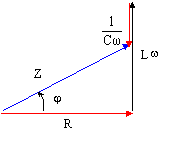
tan j = (Lw-1/Cw) / R soit R tanj =Lw-1/Cw ; Lw =R tanj +1/Cw

L =(R tanj +1/Cw) / w = (150 *tan1,35 + 1/(5 10^-6*897) / 897 = 1 H.

---

intensité efficace I

I= U/ Z avec Z²= R²+(Lw-1/(Cw)²

intensité efficace I₀ traversant le circuit à la résonance :

à la résonance l'impédance Z est minimale et vaut Z= R, d'où I₀ = U/R.

y= I/I₀ = R / [R²+(Lw-1/(Cw)²]^½= R * [R²+(Lw-1/(Cw)²]^-½

y= [1+ (Lw/R-1/(RCw))² ]^-½

or Q= Lw₀/R = 1/(RCw₀) d'où L/R= Q/w₀ et Lw/R =Qw/w₀

or x= w /w₀ d'où Lw/R = Q x .

de même : 1/(RC) = Qw₀ et 1/(RCw) = Qw₀ /w = Q/x

y = [1+ (Qx-Q/x)² ]^-½

bande passante de ce circuit : Df = Q f₀ avec f₀= 71 Hz et w₀ = 448 rad/s (voir question précédente)

or Q= Lw₀/R = 1*448 / 150 = 2,99 ; Df =2,99*71 = 212 Hz.

---

On néglige les forces de frottement et le champ magnétique terrestre.

Deux barres conductrices sont disposées parallèlement suivant la ligne de plus grande pente d'un plan incliné d'un angle a sur l'horizontale. Elles sont distante de L; leurs extrémités supérieures sont rellées entre elles par un générateur de f.e.m E et par un interrupteur K. Une barre conductrice est posée perpendiculairement sur les deux barres précédentes. Le contact électrique se fait en M et N, on le suppose parfait et de résistance nulle.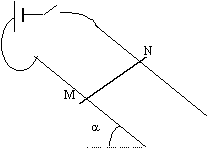

1. On crée dans la région où se trouve la barre MN un champ magnétique uniforme B perpendiculaire au plan des rails. On ferme K Quel doit être le sens de B pour que la barre MN puisse être en équilibre.
   - La barre MN a une résistance R et une masse m. Les autres résistances sont négligeables. Exprimer en fonction de E, R, L, m et a la norme de B pour que la barre soit en équilibre.
   E= 2 V ; R= 0,2 W ; L= 0,05 m ; m = 10 g ; a = 20 ° ; g=9,8 N/kg.
2. On ouvre K alors que MN est en équilibre dans le champ magnétique précédent. Montrer qu'il apparaît une tension u_MN entre les points M et N lorsque la barre descend et établir l'expression de u_MN.

---

corrigé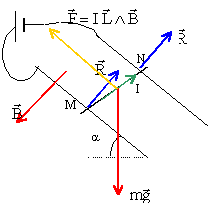

---

La tige MN est en équilibre sous l'action de son poids, verticale, vers le bas, valeur mg.

de l'action des support R, perpendiculaire au plan

de la force de Laplace F perpendiculaire au plan défini par MN et le champ magnétique B.

La somme vectorielle des forces est nulle ; cette somme s'écrit, sur un axe parallèle aux rails et dirigé vers le haut :

-mg sina + B I L=0 ; B= mg sina / (I L)

de plus E= RI soit I= E/R ; B= mg R sina / (E L).

avec : L= 0,05 m ; m= 0,01 kg ; E= 2 V ; R= 0,2 W ; a = 20 ° ; g=9,8 N/kg.

B= 0,01*9,8*0,2*sin20/(2*0,05)= 0,067 T.

---

La tige MN descent le plan à la vitesse v et parcourt en dt seconde la distance vdt.

flux du champ magnétique B à travers la surface L v dt : dF= B L v dt

Le flux varie et en conséquence une tension induite apparaît entre les points M et N telle que par ces effets électromagnétiques elle s'oppose à la variation de flux.

u_MN = dF/dt = B L v.