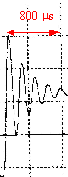|
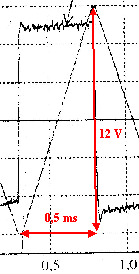
passage de Vénus devant le soleil ; autoinduction durée 3 heures ; d'après concours technicien supérieur météo 2004 |
||||
|
|
||||
|
||||
|
|
L'uranium 238 est à l'origine d'une famille radioactive qui conduit à un isotope stable du plomb 20682Pb. Les désintégrations succesives s'accompagnent d'émission de particules a ou de particules b-. La demi-vie des noyaux intermédiaires est suffisamment courtes pour que l'on puisse négliger leur présence dans les produits de la transformation ; on assimile l'ensemble à une réaction unique : 23892U -->20682Pb + xa + y b-.
corrigé 23892U -->20682Pb + x 42He + y 0-1e. conservation du nombre de nucléons : 238 = 206 + 4x soit x= 8. conservation de la charge : 92 = 82 + 2x-y soit 10=2x-y d'où y = 6. loi de décrioissance radioactive : NU(t) = NU(0) exp(-lt) soit NU(0) = NU(t) exp(lt) NPb(t) = NU(0) -NU(t) = NU(t)( exp(lt)-1) NPb(t) / NU(t) = exp(lt)-1 avec lt½ = ln 2. 1+NPb(t) / NU(t) = exp(lt) ; ln(1+NPb(t) / NU(t))= lt ; t= ln(1+NPb(t) / NU(t))/l = ln(1+NPb(t) / NU(t))/ ln2 t½. nombre de noyaux à la date t = masse (g) / masse molaire (g/mol) * nombre d'Avogadro soit NPb(t) = 0,01/ 206*A et NU(t) = 1/238 * A NPb(t) / NU(t)) = 0,01/206*238= 1,155 10-2. 1+NPb(t) / NU(t))= 1,01155 ; ln(1+NPb(t) / NU(t)) = ln 1,01155 = 1,1487 10-2. t= 1,1487 10-2 / ln 2 * 4,5 109 = 4,46 107 années.
|
|||
|
Le 8/6/04 la planète Vénus, vue de la Terre passera devant le soleil pendant à peu près cinq heures. Si cette observation est effectuée à partir de deux points A et B très éloignés sur la terre, on constate que la trace de la trajectoire de Vénus ( assimilable à un segment de droite) sur le disque solaire a une position différente suivant le lieu d'observation. 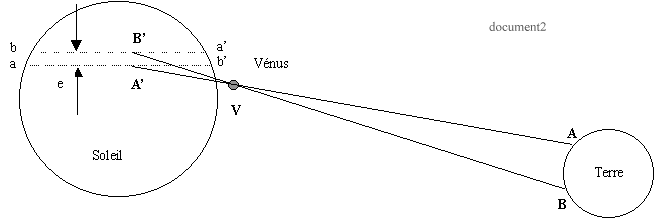 A' est la trace vue de A et B' celle vue de B. On appelle e la distance de ces deux traces. Les angles (A'VB') et (AVB) sont suffisamment petits pour que leur mesure en radians, soit assimilables respectivement à e/dSV etAB/dTV où dSV représente la distance Soleil-Vénus et dTV la distanceTerre- Vénus, AB est la distance entre les deux points d'observation. On suppose que la terre et Vénus écrivent, dans le même plan,des mouvements circulaires uniformes autour du soleil. Au moment de l'observation les planètes et le soleil sont alignés. La période de révolution de la Terre est TT= 365 jours et celle de Vénus TV= 225 jours.
corrigé Dans sa course, Vénus se retrouve tantôt entre la Terre et le Soleil (Conjonction inférieure), tantôt à l'opposé du Soleil (Conjonction Supérieure). Si le plan de l'orbite de Vénus était le même que le plan de l'orbite de la Terre autour du Soleil, il se produirait un transit, c'est-à-dire un passage de la planète devant le Soleil, à chaque Conjonction inférieure de Vénus. Mais du fait de l'inclinaison de son orbite de 3°23' par rapport à l'écliptique (le plan de l'orbite terreste autour du Soleil), le passage de Vénus devant le Soleil ne peut avoir lieu que si les trois astres sont alignés et à condition que Vénus passe au point d'intersection de son plan orbital avec l'orbite de la Terre (ligne des noeuds).
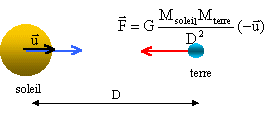
référentiel d'étude : le soleil ( héliocentrique); systéme étudué : la terre le mouvement de la terre est circulaire uniforme d'accélération centripète aN=v²/D la seconde loi de Newton s'écrit sur l'axe de vecteur unitaire u : GMsoleil Mterre / D²= Mterre v²/D d' où v² = GMsoleil / D la terre décrit une circonférence de rayon D en une période notée TT à une vitesse v. 2pD=vTT. élever au carré : 4p²D²=v²T²T. remplacer v² par l'expression donnée ci-dessus : 4p²D²= GMsoleil / DT²T. soit T²T / D3 = 4p² / (GMsoleil ) ou bien T²T / RT3 = 4p² / (GMsoleil ). 3ème loi de kepler. relation liant RT/RV et TT/TV : pour la terre : T²T / RT3 = 4p² / (GMsoleil ). pour Vénus : T²V / RV3 = 4p² / (GMsoleil ). [TT / TV ]2 = [RT /RV]3 TT2 = [RT /RV]3 TV 2. RT étant supérieur à RV, donc TT est supérieur à TV. avec les
notations du texte : TT2 = [dST /dTV]3
TV 2.
AB = e(dST -dTV) / dTV =e(dST/dTV -1) soit e = AB / dST/dTV -1) . or dST/dTV = [TT/TR]2/3 soit e= AB/ [(TT/TR)2/3-1]. e= 4 106 /((365,25/225)2/3 -1)= 1,05 107 m diamètre réel du soleil : d = 1,05 107 / 0,910-3 *0,115 =1,43 109 m = 1,34 106 km. distance Terre Soleil (Unité Astronomique) : 0,5 degré = 0,5*3,14/180 = 8,7 10-3 rad. 8,7 10-3 = diamètre soleil / distance terre-soleil distance terre-soleil = diamètre soleil / 8,7 10-3 =1,34 106 / 8,7 10-3= 1,54 108 km. distance Vénus Soleil : [TT / TV ]2 = [RT /RV]3 [TT / TV ]2/3 = RT /RV soit RV =RT /[TT / TV ]2/3 ; RV = 1,54 108 / (365,25 /225) 2/3 = 1,1 108 km
|
||||
|
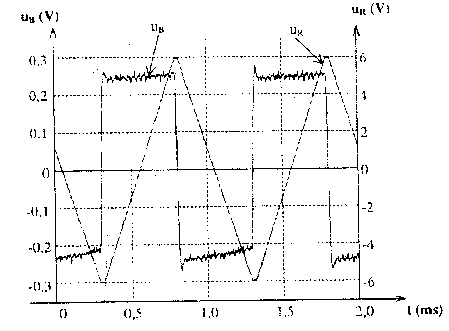
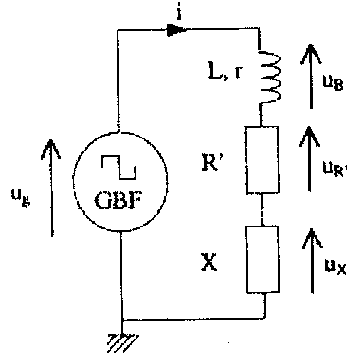
On dispose : - d'un générateur basse fréquence (GBF) dont l'une des bornes de sortie est reliée à la masse. Il délivre une tension alternative triangulaire d'amplitude Um = 6 V et de fréquence f réglable. - d'une bobine d'inductance L= 0,1 H et de résistance r = 10 W. - d'un conducteur ohmique de résistance R= 10 k W. On réalise le montage ci-dessous : 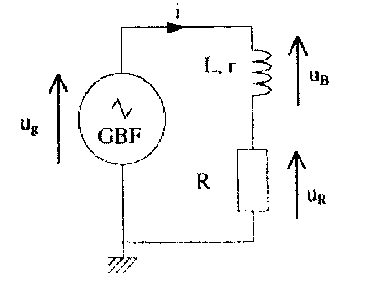
corrigé 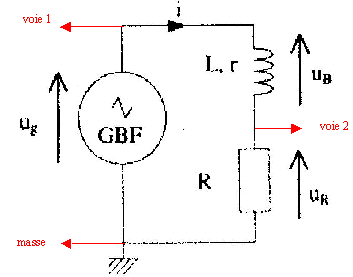
La tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles : observer uR c'est donc observer l'image de l'intensité au facteur R près. ug= uR+uB soit uB = ug- uR. de plus uB= ri + Ldi/dt. période T de l'intensité du courant = 1 ms = 10-3 s. ( lecture document 1) amplitude imax de l'intensité = uRmax/ R = 6 / 104 = 6 10-4 A. uB voisine 0,25 V ( lecture document 1)
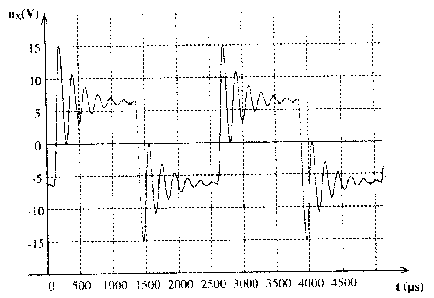
décharge oscillante d'un condensateur à travers une bobine inductive. circuit RLC en oscillations libres amorties.
environ 800 microsecondes pour 4 pseudopériodes soit T= 200 ms = 0,2 ms = 2 10-4 s. fréquence correspondante : f=1/ 2 10-4 = 5000 Hz pulsation correspondante w = 2pf = 6,28*5000 = 3,14 104 rad/s. dans le cas d'un dipôle LC, non amorti la pulsation vaut w2= 1/(LC) d'où C = 1/ (L w2) = 1/(0,1*(3,14 104)2) = 10-8 F = 10 nF.
|
||||
|
|