I.On dissout dans 500 mL d'eau distillée, 0,02 mol de fluorure d'hydrogène, composé moléculaire de formule HF.

1. Calculer la concentration en soluté apporté C₀.
2. Ce composé est l'acide d'un couple acide base. Comment s'écrit la base conjuguée ? Quel est son nom ?
3. Sachant que cet acide réagit partiellement avec l'eau, établir l'équation de la réaction acido-basique correspondante.
4. Etablir le tableau d'avancement de cette réaction.
5. Exprimer à l'état final, les concentrations en acide HF, en sa base conjuguée et en ion oxonium H₃O⁺, en fonction de C₀ et du taux d'avancement final t.
6. Exprimer pour le couple acide base la constante d'acidité Ka et montrer qu'elle s'écrit Ka = t ²C₀/(1-t)

II. Mesures pHmétriques.

A l'aide d'un pHmètre on mesure le pH de la solution aqueuse de fluorure d'hydrogène précédente. On trouve pH=2,3

1. Montrer que t = 10^-pH/C₀.
2. Déduire de la valeur du pH la valeur de t, de la constante d'acidité et du pKa.

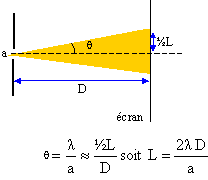
Une source mumineuse monochromatique, de longueur d'onde l inconnue, est placée devant une fente de largeur a= 0,1 mm. A une distance D= 2,6 m de cette fente on place un écran. Sur l'écran onobserve la figure ci-dessous représentée à l'echelle réelle.

I. Questions préliminaires.

1. Comment se nomme le phénomène observé ?
   On rappelle la relation liant l'angle q fait par la direction initiale du faisceau avec la première extinction, la longueur d'onde et la largeur de la fente : q voisin l /a.
2. Faire un schéma prècis du dispositif utilisé en y faisant apparaître D, q et d, largeur de la tache centrale.
3. Il est possible, pour un tel phénomène, d'établir une relation entre q, D, a et d. Parmi les relations ci-dessous dans lesquelles k est une constante, montrer par une analyse dimensionnelle, que les relations b et c ne peuvent pas convenir.

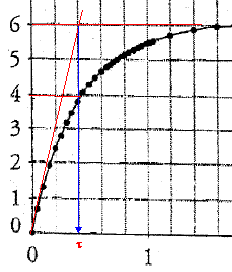
II. Détermination de la constante k.

On remplace dans le dispositif précédent la source monochromatique par un laser vert de fréquence f= 5,7 10¹⁴ Hz et la fente, successivement par des fils calibrés de diamètre a connus, l'écran restant à la même distance D.On admet que les résultats obtenus avec une fente de largeur a restent inchangés pour les fils ( le diamètre des fils correspond à la largeur de la fente). On mesure pour chaque fil la largeur d de la tâche centrale de diffraction observée sur l'écran. On obtient le graphe suivant , sur lequel x= 1/a, exprimé en mm^-1, est porté en abscisse et d, exprimée en mm, est portée en ordonnée.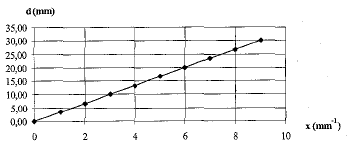

1. Calculer la longueur d'onde du laser de couleur verte.
2. Calculer le coefficient directeur de cette droite ; quelle est son unité ?
   En déduire la valeur de la constante k.

III. Détermination de la longueur d'onde inconnue :

1. Sur la figure obtenue avec la source lumineuse de longueur d'onde l, mesurer bord à bord, la largeur d de la tâche centrale.
2. En déduire la valeur de la longueur d'onde l ainsi que la couleur de la lumière émise par cette source.

Donnée : c= 3 10⁸ m/s.

Le circuit ci-dessous est constitué d'un générateur, délivrant un échelon de tension E= 6 V, d'une bobine d'inductance L et d'un conducteur ohmique de résistance R= 120 W.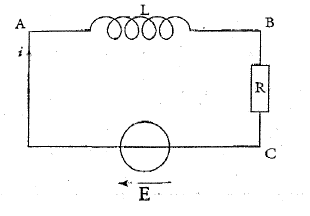

A. Visualisation à l'oscilloscope :

1. Faire apparaître les branchements à effectuer pour visualiser simultanément, sur l'écran de l'oscilloscope, la tension u_G aux bornes du générateur, en voie 1 et la tension u_R, aux bornes du conducteur ohmique, en voie 2.
2. L'une de ces tensions permet de déduire les variations de l'intensité du courant dans le circuit. Laquelle ? Justifier.
3. Sur l'une des voies on observe la tension U.
   - Cette tension U correspond-elle à celle visualisée voie 1 ou bien voie 2 ?
   - Quel phénomène l'observation de la tension U met-elle en évidence ? Quel est l'élément responsable ?
4. Déduire de la courbe représentative de U l'intensité I₀ du courant en régime permanent.

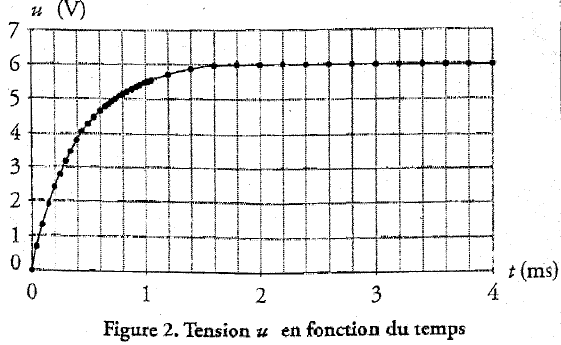B. Constante de temps du dipôle RL :

1. La constante de temps t est donnée par t = L/R; Déterminer à partir de la figure 2, par la méthode la plus appropriée, la constante de temps du dipôle.
2. En déduire la valeur de l'inductance de la bobine.

C. Equation différentielle du circuit :

1. L'équation différentielle du circuit, relative à i, étant Ldi/dt + Ri = E, vérifier que cette équation différentielle admet pour solution la fonction i(t) = A(1 - exp(-Bt)) à condition de poser A= E/R et B= R/L.
2. Exprimer la valeur de i(t) quand t= 5t . Conclure.

---

corrigé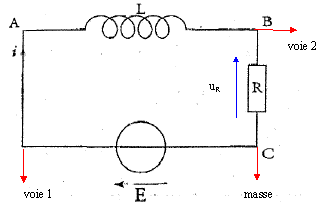

---

La tension aux bornes d'un résistor est proportionnelle à l'intensité. u_R est donc l'image de l'intensité au facteur R près.

U correspond à u_R, tension visualisée sur la voie 2 : on observe un retard à l'établissement du courant, retard pendant lequel la bobine stocke de l'énergie ; phénomène d'autoinduction dû à la bobine inductive.

I₀ = 6 / R = 6 / 120 =0,05 A.

---

t = 0,4 10^-3 = L/R soit L= 120*4 10^-4 = 4,8 10^-2 H = 48 mH.

---

Ldi/dt + Ri = E (1)

i(t) = A(1 - exp(-Bt)) ; di / dt = AB exp(-Bt)

repport dans (1) : LAB exp(-Bt) + RA(1 - exp(-Bt)) =E

LAB exp(-Bt) +RA-RAexp(-Bt) = E

A(LB-R)exp(-Bt) +RA=E

par identification : RA = E soit A= E/R= 6 / 120 = 0,05A = I₀.

et LB-R =0 soit B= R/L = 1/t

i(5t) = I₀(1 - exp(-5))=I₀(1 - 6,7 10^-3)=0,993 I₀.

Le régime permanent est pratiquement atteint.

---