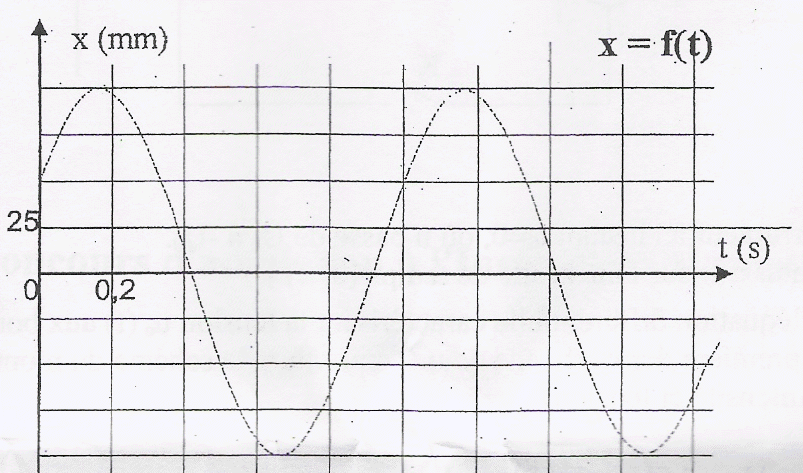Aurélie 04/05
trajectoire d'une boule de pétanque;

datation : potassium argon ; oscillateur mécanique ; condensateur ; sulfate de baryum ; pile électrique ; ester ; caféine ; vert de malachite.

sans calculatrice ; d'après concours kiné Limoges 2005

Google

trajectoire d'une boule de pétanque (3 points)

 Un joueur de pétanque lance une boule de masse m d'un point A situé à une hauteur OA= 0,7 m au dessus du sol. a= 60 °. La boule atteint le sol horizontal à une distance d= 10 m de la verticale du point A.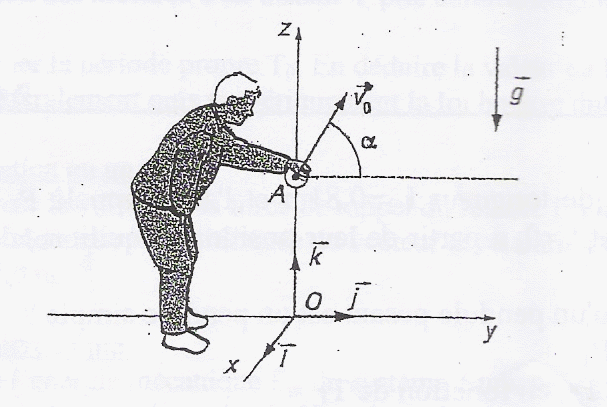

  1. Déterminer l'équation de la trajectoire du centre d'inertie G de la boule dans le repère ci-dessus.
  2. Calculer la valeur de la vitesse initiale.

g= 10 m/s² ; cos 60 = 0,5 ; tan 60 = 1,73 ; racine carrée (1000)= 31,5.

 

corrigé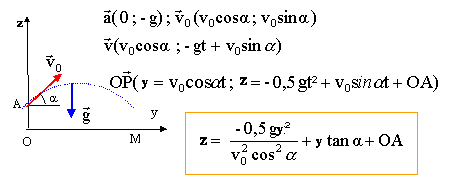

Au point d'impact y=0 et x=d=10 m.

0= -0,5*10*100/(v0²*0,5²)+ 10 *1,73 + 0,7

0= -2000/v0² + 18 soit v0² = 1000/9 ; v0 =31,5 / 3 = 10,5 m/s.
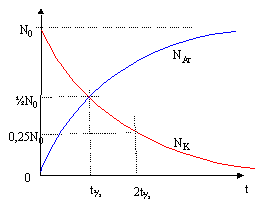
datation par la méthode du potassium argon :(5 points)

Le potassium K( Z= 19 et A= 40) est radioactif et se désintègre en donnant de l'argon Ar( Z= 18 ; A= 40)

  1. Ecrire l'équation de cette désintégration nucléaire en précisant les lois de conservation utilisées et nommer les produits obtenus.
  2. Exprimer en fonction du temps le nombre NK d'atomes de potassium 40 et NAr d'atomes d'argon 40 présents à un instant t dans un échantillon contenant initialement N0 atomes de potassium 40.
  3. Représenter sur un même graphique les courbes NK= f(t) et NAr = g(t).
  4. Certaines roches volcaniques contiennent du potassium dont une partie est du potassium 40. Au moment de sa formation, cette roche ne contient pas d'argon. Un géologue analyse un échantillon de cette roche et constate que les atomes d'argon 40 y sont deux fois moins nombreux que les atomes de potassium 40. Déterminer l'âge de la roche.

l= constante radioactive du potassium 40

demi vie du potassium 40 : t½= 1,5 109 ans

ln 2 = 0,7 ; ln 3 = 1,1 ; 4/7 voisin 0,6. 

corrigé
4019K-->4018Ar + 01e ( positon)

conservation de la charge : 19 = 18 + 1

conservation du nombre de nucléons : 40 = 40 +0

loi de décroissance radioactive : NK= N0 exp(-lt) où N0 = NKexp(lt)

en conséquence NAr = N0-NK=N0 (1-exp(-lt))

NAr=½NK ; (N0-NK)=½NK ;(N0-NK) /NK = 0,5 soit N0/NK = 1,5.

d'après la loi de décroissance radioactive :NK/ N0 = exp(-lt)

ln(NK/ N0 )= -lt ; N0 /NK =lt

d'où : lt = ln1,5 avec lt½=ln2

soit t = ln1,5 / ln2 *t½= (ln3-ln2)/ln2*t½= (1,1-0,7)/0,7*1,5 109 =4/7 *1,5 109 =0,6*1,5 109 = 0,9 109 ans.

Deux pendules simples :(2 points)

Deux pendules simples, l'un appelé P1 de longueur L1= 0,81 m et l'autre appelé P2 de longueur L2 = 2,56 L1, sont lancés au même moment à partir de leur position d'équilibre dans le même sens noté "+".

  1. A quelles conditions peut-on dire qu'un pendule pesant est un pendule simple ?
  2. Calculer T1, la période du pendule P1.( g= 10 m/s² ; racine carrée 10 =p)
  3. Exprimer T2, période du pendule P2 en fonction de T1. 16² = 256
  4. Au bout de combien de temps les deux pendules repassent-ils simultanément dans le même sens "+" pour la première fois par leur position d'équilibre ?.
corrigé
Un solide ponctuel,de masse m, accroché à une fil inextensible de masse négligeable, constitue un pendule simple.

T1 = 2p (L1/g)½= 2p (0,81 / 10 )½=2p 0,81½ / 10 ½=2p * 0,9 /p = 1,8 s.

T2 = 2p (L2/g)½ ;T2 /T1 =(L2/L1)½ ;T2 =T1 (L2/L1)½ =T1 (2,56)½ =1,6T1.

Lorsque le pendule P1 décrit n périodes, alors le pendule P2 décrit n' périodes : les deux pendules passent alors pour la première fois , dans le même sens "+" à la position d'équilibre.

n T1 = n'T2 soit n T1 = n'*1,6 T1 ; n= 1,6 n' avec n et n' entiers

n'=5 et n=8 ; le temps vaut : 1,8*8 = 14,4 s.
oscillateur mécanique :(5 points)

Un mobile autopoerteur de masse m =500 g se déplace sur une table horizontale. Il est accroché à deux ressorts métalliques identiques, de masse négligeable, de longueur au repos l0, et de constante de raideur k. A1 et A2 sont des points fixes. On admet que le dispositif est équivalent à un mobile autoporteur de masse m fixé à un ressort unique de constante de raideur K= 2k dont l'autre extrémité est fixe.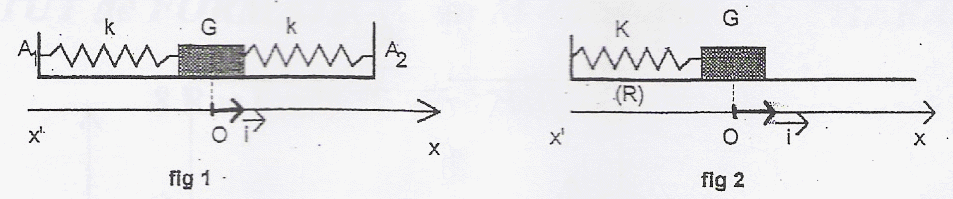

  1. On écarte le mobile de sa position d'équilibre et on le lâche sans vitesse initiale. Après quelques oscillations, on déclenche l'acquisition des mesures à un instant t choisi comme origine des dates. On obtient l'enregistrement ci-dessus.
    - Déterminer la période T0 et en déduire la constante de raideur de chaque ressort.( p ² = 10)
    - Ecrire littéralement puis numériquement la loi horaire du mouvement de x(t).
  2. Déterminer la valeur de la force de rappel du ressort à la date t= 1 s.
    - Montrer alors que l'accélération du mobile à cette date est ax= -2 m/s².
  3. Calculer l'énergie mécanique Em du système équivalent { ressort + mobile}
    - Déterminer la vitesse maximale Vm du mobile.
    - Que vaut l'énergie potentielle élastique Ep de ce système à la date t= 1 s.
    - En déduire la valeur de la vitesse V à cet instant. Quel est le sens du vecteur vitesse ?
    racine carrée (0,4) = 0,63 ; racine carrée (0,3)= 0,55).
corrigé
période T0 : 5 divisions soit 5 *0,2 = 1 s.

T0 = 2 p (m/(2k))½ soit 2k = 4 p ²m /T²0 =4*10*0,5 / 1 =20 soit k = 10 N/m.

x(t) = xmax sin( w t+j) avec xmax = 100 mm = 0,1 m

w =2 p /T0 =2 p rad/s ; j : phase à l'origine des temps.

x(0) = 50 mm = 0,05 m (lecture graphe) ;x(0) = 0,1 sinj d'où sin j =0,05/0,1 = 0,5 ; j=30° ou 0,52 rad.

x(t) = 0,1 sin (2 p t +p /6).

les vecteurs sont écrits en gras et en bleu.

force de rappel : F= - 2k x i = -2k 0,1 sin (2 p t +p /6) i = -2 sin (2 p t +p /6) i.

valeur de la force de rappel à t = 1 s : 2 sin (2 p +p /6) = 2 sin(p /6) = 1 N.

l'accélération est la dérivée seconde de x(t) par rapport au temps :

x'(t) = 0,1*2p cos (2 p t +p /6)

x"(t) = -0,1*(2p)²sin (2 p t +p /6) = - (2p)² x(t)

à t = 1 s : : x"(1) = -0,1 *4p2 sin(2 p t +p /6) = -0,1*4*10 sin(p /6) = -4 *0,5 = -2 m/s².

Lorsque x(t) est maximale, l'énergie mécanique est sous forme potentielle élastique.

En absence de frottement, l'énergie mécanique reste constante : Em = ½(2k) x²max = 0,5*20*0,1² =0,1 J.

Au passage à la position d'équilibre, l'énergie mécanique est sous forme cinétique ( la vitesse est alors maximale)

0,1 = ½mV²max soit V²max =0,2 / m = 0,2 /0,5 = 0,4 ; Vmax = 0,63 m/s.

Ep(t=1) = ½(2k)x²(t=1) = k x²(t=1) = 10 x²(t=1) = 10 *0,1² sin² (2 p +p /6)= 0,1 sin²(p /6) = 0,1*0,5²= 0,025 J.

vitesse à t= 1 s : x'(t) = 0,1*2p cos (2 p +p /6) =0,1*2p cos (p /6)= 0,1*2p * 0,87 = 0,55 m/s.

La vitesse correspond à la pente ( coefficient directeur) de la tangente à la courbe à la date t= 1 s : ce coefficient directeur est positif, donc la vitesse à le sens du vecteur i.

électricité : (5 points)

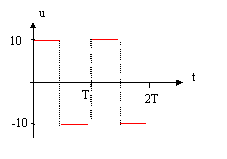
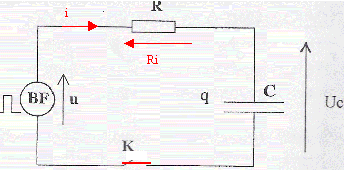
On réalise le montage ci-dessous permettant d'étudier la charge et la décharge d'un condensateur ( C= 10 mF; R= 10 kW). Le générateur basse fréquence délivre une tension u alternative crénau, d'amplitude U0 = 10V et de période T. Initialement l'interrupteur K est ouvert et la tension aux bornes du condensateur est + 5 V.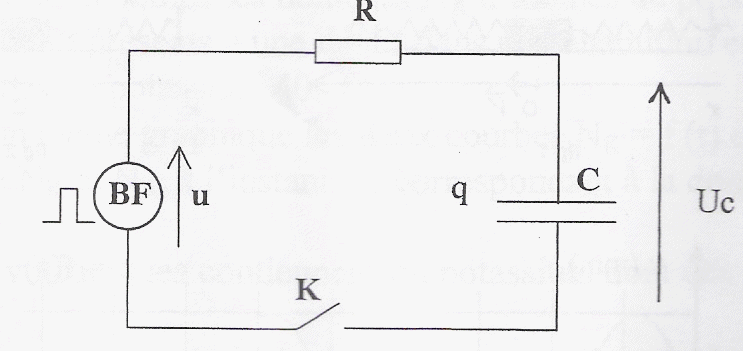

  1. On ferme l'interrupteur à l'instant t=0 où u passe de la valeur U0 à - U0.
    - Représenter u(t) sur l'intervalle [0 , 2T]
    - Etablir l'équation différentielle caractérisant la tension uc(t) aux bornes du condensateur pendant la première demi-période de u.( Reproduire le schéma du montage en faisant apparaître l 'intensité et la tension).
  2. On donne uc= -U0+ 1,5 U0 exp(-t/(RC)) (1).
    - Montrer que pendant la première demi-période de u, l'expression (1) est bien solution de l'équation différentielle établie ci-dessus et qu'elle vérifie la condition initiale à t=0.
  3. Déterminer la période de la tension délivrée par le générateur sachant qu'après une demi-période uc= -½U0.
  4. Ecrire l'équation différentielle caractérisant uc pendant la seconde demi-période.
    - On donne pour cette demi-période uc= U0- 1,5 U0 exp((T-2t)/(2RC)) (2).
    L'expression (2) est une solution de l'équation différentielle caractérisant uc pendant la seconde demi-période. Calculer la valeur de uc à l'instant du début de cette demi-période.
    - Montrer qu'à la fin de cette demi-période uc= ½U0.
    - Tracer l'allure de la courbe uc(t) sur l'intervalle [0, T].
    ln(3)= 1,1 .

corrigé

Ri + uc= u = -U0 avec i= dq/dt = d(Cuc)/dt = Cduc/dt = Cu'c.

d'où RCu'c + uc= -U0.

uc= -U0+ 1,5 U0 exp(-t/(RC))

dériver par rapport au temps : u'c=- 1,5 U0 / (RC)exp(-t/(RC))

repport dans l'équation différentielle :

- 1,5 U0 exp(-t/(RC)) -U0+ 1,5 U0 exp(-t/(RC)) = - U0 vérifiée pour toute valeur de t.

uc(t=0 ) =-U0+ 1,5 U0 = 0,5 U0 = 0,5*10 = 5 V ( condition initiale vérifiée)

après une demi-période uc(t=½T)= -½U0.

uc= -½U0= -U0+ 1,5 U0 exp(-T/(2RC)) avec RC= 104*10-5 = 0,1 s.

-0,5 = -1 + 1,5 exp (-T/ 0,2) ; 0,5 / 1,5 =exp (-T/ 0,2) ; 1/3 =exp (-T/ 0,2)

ln 3 =T/ 0,2 soit T= 0,2 ln3 = 0,2*1,1 = 0,22 s.

Ri + uc= u = U0 avec i= dq/dt = d(Cuc)/dt = Cduc/dt = Cu'c.

d'où RCu'c + uc= U0.

uc= -U0- 1,5 U0 exp((T-2t)/(2RC))

valeur de uc à la date t= 0,5 T :

uc(t= 0,5 T)= U0- 1,5 U0 exp((T-T)/(2RC)) =U0- 1,5 U0 = -½U0.

valeur de uc à la date t= T :

uc(t= T)= U0- 1,5 U0 exp((T-2T)/(2RC)) =U0- 1,5 U0 exp((-T)/(2RC)) avec :T/(2RC) =0,22 / (0,2) = 1,1 s.

uc(t= T)= U0- 1,5 U0 exp(-1,1) =U0- 1,5 U0(1/3) = ½U0.
solubilité de sulfate de baryum :(1 point)

Le sulfate de baryum BaSO4 est un composé très peu soluble dans l'eau. 

  1. Ecrire l'équation de sa dissolution.
  2. La constante d'équilibre de la réaction précédente K= 10-10 à 25°C. Déterminer les concentrations molaires de chacun des ions baryum et sulfate présents dans une solution aqueuse saturée.
  3. On ajoute dans une solution saturée homogène et limpide de sulfate de baryum une goutte d'acide sulfurique concentré H2SO4 ce qui ne fait pas sensiblement varier son volume. Que se passe-t-il dans la solution ? Justifier à partir du critère d'évolution spontané.
corrigé
BaSO4 (s) = Ba2+(aq) + SO42-(aq)

K= [Ba2+][SO42-]=10-10

[Ba2+]=[SO42-]= K½= 10-5 mol/L.

état initial : on ajoute à la solution saturée une goutte d'acide sulfurique donc des ions sulfates ; en conséquence le quotient initial Qr, i devient supérieur à K : la transformation évolue donc dans le sens indirect, précipitation du solide BaSO4.
pile électrique :(4 points)

 

Dans un bécher on mélange 20 mL de solution de nitrate d'argent Ag+ ; NO3- de concentration 0,1 mol/L avec 20 mL d'une solution de nitrate de cuivre Cu2+ ; 2NO3- de concentration 0,05 mol/L.

La constante d'équilibre associée à la réaction 2Ag+ (aq)+ Cu(s) = 2Ag(s) + Cu2+(aq) vaut K= 2 1015.

Masse atomique molaire (g/mol ): Cu : 64 ; Ag : 108. 1 faraday = 105 C.

  1. Calculer la valeur initiale du quotient de réaction. En déduire le sens d'évolution de celle-ci. Par quelle remarque qualitative peut-on remarquer qu'il en est ainsi ?
    - Lorsque le système atteint l'équilibre, la concentration en ion Cu2+ est 0,05 mol/L. Calculer la concentration en ion Ag+ et conclure.
  2. On considère une pile électrique constituée avec les mêmes solutions contenues dans des récipients reliés par un pont salin et des lames de métaux appropriés.
    - Les deux électrodes de cette pile sont reliées par un conducteur ohmique. Donner les demi-équations de réactions aux électrodes. En déduire la polarité de la pile.
    - Les masses des électrodes de cuivre et d'argent sont respectivement 0,64 g et 1,08 g. Le volume de chaque solution est 20 mL. Construire le tableau décrivant l'avancement de la réaction..
    - Quel est le réactif limitant ?
    - Quelle quantité d'électricité a traversé le conducteur quand la pile s'arrête de fonctionner ?
corrigé
Qri = [Cu2+]i/[Ag+]i2avec [Cu2+]i = 0,05*20/40 = 0,025 mol/L et [Ag+]i = 0,1*20/40 = 0,05 mol/L

Qri =0,025/0,05²= 250/25=10.

Qri <K donc évolution dans le sens direct.

Qr éq = K = [Cu2+]éq/[Ag+]éq2

[Ag+]éq2 = [Cu2+]éq//K= 0,05 / 2 1015 = 25 10-18 mol/L ; [Ag+]éq = 5 10-9 mol/L

l'ion argent a pratiquement disparu ; ce dernier constitue le réactif limitant.

réduction à la cathode positive : 2Ag+ (aq) + 2e- = 2Ag (s)

oxydation à l'anode négative : Cu(s) = Cu2+ (aq) + 2e-.
2Ag+
+ Cu(s) =
2Ag (s)
+ Cu2+
t=0
0,02*0,1=2 10-3 mol
0,64/64 = 0,01 mol
1,08/108 = 0,01 mol
0,02*0,05 = 10-3 mol
en cours
2 10-3 -2x
0,01-x
0,01+2x
10-3 +x
fin
0
0,01-xmax = 9 10-3
0,01+2xmax =1,2 10-2
10-3 +xmax =2 10-3 mol
xmax = 10-3 mol

Or Ag+ (aq) + e- = Ag (s) d'où la quantité de matière d'électrons : 10-3 mol

La charge, en valeur absolue, d'une mole d'électrons vaut 105 C

Qté d'électricité ayant traversé le conducteur : 10-3*105 = 100 C.
estérification :

 Le géraniol est un alcool primaire de formule brute C10H18O. On réalise la synthèse de l'acétate de géranyle à partir du géraniol et de l'anhydride acétique. On dispose d'une masse m1 = 1,54 g de géraniol et d'un volume V= 10,2 mL d'anhydride acétique ( r= 1,08 g)mL).

Masse molaire en g/mol : M( géraniol) = 154 ; M( ester) = 196 ;M( acide acétique) = 60

  1. Ecrire l'équation de la réaction chimique.
    - Pour quelles raisons utilise-t-on l'anhydride acétique plutot que l'acide acétique comme réactif ?
    - Calculer à partir des données la masse molaire de l'anhydride acétique.
  2. Déterminer l'expression de la quantité de matière d'anhydride acétique en fonction de M( anhydride), V et r.
    - Faire l'application numérique.
  3. Déterminer l'avancement maximal de la réaction.
    - Quelle masse d'acétate de géranyle peut-on théoriquement obtenir ?
corrigé
C10H18O + (CH3-CO)2O --> CH3-CO2-C10H18 + CH3-CO2H

réaction totale et rapide avec l'anhydride, lente et limitée avec l'acide acétique.

masse des produits = masse des réactis

soit à partir d'une mole d'alcool et d'une mole d'anhydride :

M( anhydride) + M( géraniol) =M( ester) +M( acide acétique)

M( anhydride) = - M( géraniol) +M( ester) +M( acide acétique) = -154+196+60 = 102 g/mol.

n( anhydride) = masse (g) / masse molaire avec masse (g) = masse volumique (g/mL) * volume (mL)

n( anhydride) = r V/M(anhydride) = 1,08*10,2/102 = 0,108 mol.

n ( géraniol) = m1/ M( géraniol) = 1,54 / 154 = 0,01 mol.

l'alcool est le réactif limitant : xmax = 0,01 mol

on peut obtenir théoriquement 0,01 mol d'ester soit : 0,01*196 = 1,96 g.
solution de caféine :(2 points)

La caféine est une base dont le couple acide base sera noté BH+/B. On dissout 0,01 mol de caféine dans de l'eau distillée de façon à avoir un volume V=500 mL de solution. La conductivité de la solution vaut s = 40 mS m-1.

Conductivité molaire ionique en mS m² mol-1 : lBH+ = 0 ; lHO- = 20 ; Ke = 10-14 et log 2 = 0,3.

  1. Ecrire l'équation de dissolution de la caféine dans l'eau.
  2. Calculer l'avancement final de cette réaction.
    - Calculer le taux d'avancement.
  3. Calculer le pH de cette solution.
corrigé
B +H2O = BH+ + HO-.

s = lBH+ [BH+]+ lHO- [HO-] avec [HO-] =[BH+]

s = (lBH+ +lHO- ) [HO-] ; [HO-]= s / (lBH+ +lHO- ) 40 / 20 = 2 mol m-3 = 2 10-3 mol/L

soit n( HO-) =xfin = 2 10-3 * 0,5 = 10-3 mol.

x max = 0,01 mol soit t = xfin / x max = 10-3 / 10-2 = 0,1 .

[H3O+]=Ke / [HO-]= 10-14 / 2 10-3 = ½ 10-11.

pH = - log [H3O+] = 11+log2 = 11,3.
le vert de malachite : 1 point

 Le vert de malachite est un indicateur coloré dont le pka du couple cpnstitué par la forme acide et la forme basique notées A et B vaut 1,3. La couleur donnée par la forme acide A est jaune et celle donnée par la forme basique est bleu vert.

  1. Quelle est la couleur prise par une solution de pH=2,8 contenant du vert de malachite. Justifier.
  2. Calculer le rapport de concentrations des formes basique et acide. On prendra racine carrée (10)= 3,1.
corrigé
à pH > pKa la forme basique prédomine.

à pH>pKa+ 1, la forme basique est au moins 10 fois plus importante que le forme acide :

donc la couleur de la solution est bleu vert.

pH = pKa + log ( B/A) ; log (B/A) = pH-pKa = 2,8-1,3 = 1,5

B/A = 101,5 = 103/2 = racine carrée(1000)= racine carrée 100 * racine carrée 10 = 10*3,1 = 31.

retour -menu