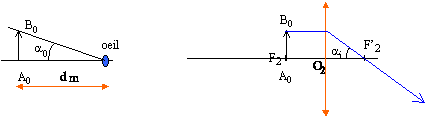Aurélie dec 04

freinage d'un cylindre ; microscope ; circuit RLC parallèle ; densitomètre ; moteur thermique ; réseaux électriques

d'après concours ICNA 2004





Google



mécanique : freinage d'un cylindre

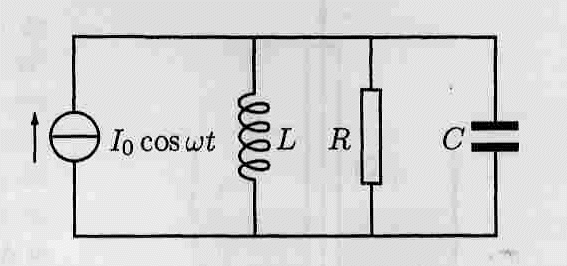
Un cylindre homogène (C) de centre de masse G, de rayon a et de masse m roule sans glisser sur un plan horizontal xOy. Le vecteur rotarion instantané w porté par son axe de révolution est constamment dirigé suivant l'axe Oy. On désigne par T= Tex et N= Nez les composantes tangentielle et normale de la réaction du plan xOy sur le cylindre.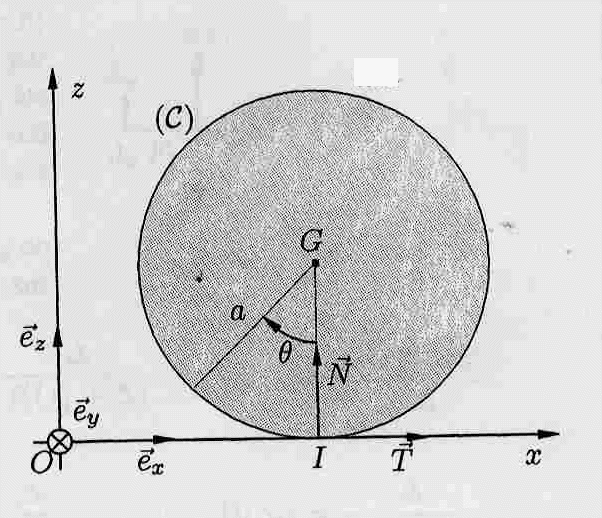

La rotation de (C) est repérée par l'angle orienté q défini sur la figure ci-dessous. On désigne par xG l'abscisse du centre de masse G et par J= ½ma² le moment d'inertie du cylindre par rapport à l'axe Gy.

A l'instant t=0 où l'axe du cylindre passe dans le plan xOy la norme de la vitesse du centre de masse est v0. On applique alors un couple de freinage de moment constant, Cf= - Cf ey ( les vecteurs sont écrits en bleu et en gras) dont l'intensité est telle que (C) continue de rouler sans jamais glisser. On suppose que l'effet de ce couple sur les valeurs de T et N est négligeable.

  1. Calculer l'énergie cinétique initiale du cylindre Ec0.
  2. Déterminer la loi d'évolution de la vitesse de translation v(t) du cylindre en fonction du temps.
  3. Calculer la distance de freinage x0.
  4. Sachant que le cylindre roule sans glisser tant que la relation T<fN, où f est une constante caractéristique de l'adhérence du cylindre, est vérifiée, trouver la distance mi,imale de freinage x0min de (C).
  5. Au cours du freinage, la température du cylindre et celle du système de freinage s'élève. Calculer la quantité de chaleur algébrique Q échangée avec le milieu extérieur pour que la température de l'ensemble revienne à la valeur initiale.
  6. A l'insatnt t=0, le couple de freinage est tel que le cylindre se bloque et glisse instantanément. Calculer la nouvelle distance de freinage x1.
corrigé
énergie cinétique de rotation : ½Jw² avec J= ½ma² et v= w a

énergie cinétique de translation : ½mv²

Ec0 =½Jw²+ ½mv² = ½ (½ma²)v²/a² + ½mv² = 0,75 m v².

Le cylindre est soumis à son poids P, vertical vers le bas, à l'action normale du plan, à l'action tangentielle du plan et au couple de freinage.

Le poids et l'action normale du plan ont des directions qui rencontrent l'axe Gy : le moment de ces forces par rapport à l'axe Gy est nul.

Moment de T par rapport à cet axe Gy : -T a ( n'intervient que dans le cas d'un glissement)

somme de moments = Jq" avec q" = w ' =v'/a

-Cf = Jv'/a avec J=½ma²

- Cf = ½mav' ; v' = -2/m (Cf/a)

par intégration: v = -2/m ( Cf/a) t + constante.

à t=0 v(t)= v0 d'où la constante : v(t)= v0-2/m (Cf/a) t.

distance de freinage ( sans glissement)

le travail du couple de freinage est égal à la variation de l'énergie cinétique : -Cfq = 0-0,75mv0².

q = 0,75mv0² / Cf avec q a= x0 soit x0 = 0,75 mav0² / Cf .

La distance minimale de freinage correspond au cas où le cylindre se bloque à l'instant t=0

le cylindre ne roule plus mais glisse : son énergie cinétique est ègale à l'énergie cinétique de translation ½mv0².

le travail de T, action tangentielle du plan est égal à la variation de l'énergie cinétique : -Tx0 min = 0-0,5mv0².

avec T= f N et N= mg soit x0 min = 0,5 v0² / (fg) .

Pour que la température de l'ensemble revienne à la valeur initiale, la quantité de chaleur algébrique Q échangée avec le milieu extérieur est :
négative, le système cède de l'énergie au milieu extérieur

sa valeur est égale à l'énergie cinétique initiale Q= - 0,75 mv0².

distance de freinage ( glissement)

à t = 0, le cylindre ne roule plus mais glisse : son énergie cinétique est ègale à l'énergie cinétique de translation ½mv0².

le travail de T, action tangentielle du plan est égal à la variation de l'énergie cinétique : -Tx1 = 0-0,5mv0².

avec T= f N et N= mg soit x1 = 0,5 v0² / (fg) .

circuit RLC parallèle

 R= 100 W ; C= 100 mF ; L= 10 mH ; la pulsation w peut varier de façon continue. I0 , valeur efficace = 100 mA.

On désigne par w 0 la valeur de la pulsation pour laquelle la puissance moyenne P fournie au circuit par la source, calculée sur une période, passe par une valeur maximale Pmax. On pose x= w /w0.

  1. Si Q désigne une constante, montrer que l'on peut écrire : P= Pmax / [1+Q²(x-1/x)²]
  2. Calculer numériquement w0 et Pmax.
  3. Donner la valeur numérique de Q.
  4. La bande passante Dw0 du circuit est définie par la différence des pulsations pour lesquelles la puissance vaut Pmax/2. Calculer la valeur numérique de Dw0 .
  5. Montrer que l'intensité du courant dans la bobine peut s'écrire : iL(t) = IL cos(wt+jL). Exprimer IL.
  6. Montrer que IL passe par une valeur maximum ILmax pour une valeur w1 de la pulsation, si Q> Qmin. Exprimer Qmin.
  7. Exprimer w1.
  8. Donner l'expression de ILmax
corrigé
toutes les grandeurs soulignées sont des nombres complexes associés aux grandeurs physiques.

résistor : impédance : R ; admittance 1/R

condensateur : impédance 1/(jCw) ; admittance : jCw

bobine : impédance : jLw ; admittance : 1/(jLw )= -j/(Lw)

en parallèle, les admittances s'ajoutent : A= 1/R + j[ Cw - 1/(Lw)]= [1+jR[ Cw - 1/(Lw)]]/R

impédance Z= 1/A = R / [1+jR[ Cw - 1/(Lw)]]

multiplier par l'expression conjuguée :

Z= R [1-jR[ Cw - 1/(Lw)]]/ [1 + R²[ Cw - 1/(Lw)]²]

on pose LCw0²= 1 ; x= w /w0 ; Z= R [1-jR[ Cxw0 - 1/(Lxw0)]]/ [1 + R²[ Cxw0 - 1/(Lxw0)]²]

Z= R [1-jRCw0[ x - 1/(LCxw²0)]]/ [1 + R²C²w²0[ x - 1/(LCxw²0)]²]

Z= R [1-jRCw0[ x - 1/(x)]]/ [1 + R²C²w²0[ x - 1/(x)]²]

Z= R [1-jQ[ x - 1/(x)]]/ [1 + Q²[ x - 1/(x)]²]

Z²= R²(1 +Q²[ x - 1/(x)]² )/ [1 + Q²[ x - 1/(x)]²]² = R² / [1 + R²C²w²0[ x - 1/(x)]²]½

Z= R / [1 + R²C²w²0[ x - 1/(x)]²] ½ = R / ( 1+Q²(x - 1/x)²)½ avec Q= RCw0.

Puissance moyenne P = partie réelle ( ½ui*) = partie réelle ( ½ZI²max)

P= ½ I²max R / ( 1+Q²(x - 1/x)²) avec I²0 = ½ I²max

P = R / ( 1+Q²(x - 1/x)²) I²0

la puissance est maximale lorsque Z est maximale (soit pour x=1) et vaut Zmax= R

Pmax = ½RI²max = RI²0 ; P = Pmax / ( 1+Q²(x - 1/x)²)

w0²= 1/ (LC) = 1/ (10-4*10-2)= 106 ; w0= 1000 rad/s.

Pmax = RI²0 = 100*0,1² = 1 W.

Q= RCw0= 100 * 10-4 * 103 = 10.

bande passante :

aux limites de la bande passante P= ½Pmax : ½Pmax = Pmax / ( 1+Q²(xL - 1/xL)²)

2= 1+Q²(xL - 1/xL)² ; 1 = Q²(xL - 1/xL)²=0 ; 0,01 = (xL - 1/xL)²=0 ;

(xL - 1/xL)= 0,1 et (xL - 1/xL)= - 0,1

x²L - 0,1 xL -1 = 0 et x²L + 0,1 xL -1 = 0

solutions : x1= 1,05 et x2= 0,95

w1= 1,05 w0 ; w2 = 0,95 w0 ; Dw= 0,1 w0 = 0,1*1000 = 100 rad/s.

intensité du courant dans la bobine :

 u : tension complexe aux bornes d'un dipôle en parallèle ; i intensité du courant principal, nombre réel.

u = Z i = jLw iL = jLxw0 iL =jLxw0 iL = j x/ (Cw0) iL

iL= -jZ i Cw0 /x = -j R Cw0 /x [1-jQ[ x - 1/(x)]]/ [1 + Q²[ x - 1/(x)]²] i

iL= Q/x [-j +Q[ x - 1/(x)]]/ [1 + Q²[ x - 1/(x)]²] i

IL= Q/(x [1 + Q²( x - 1/x)²]½)Imax.

ILmax est maximum si x [1 + Q²( x - 1/x)²]½ est minimum :

x ²[1 + Q²( x - 1/x)²] soit y = x² + Q²(x²-1)² minimum

la dérivée de y doit s'annuler : 2x + 4Q² x(x²-1)=0 ; x²= (2Q²-1) / (2Q²).

2Q²-1 doit être positif ou nul soit Qmin >=2-½.

Expression de w1 :

x= w1 /w0 = [(2Q²-1) / (2Q²)]½ ; w1 = w0[(2Q²-1) / (2Q²)]½

Expression de ILmax :

ILmax = Q/([x² + Q²( x² - 1)²]½)Imax.

([x² + Q²( x² - 1)²]½) = [ (2Q²-1) / (2Q²) + Q²( (2Q²-1) / (2Q²) -1)²]½

ILmax = ½(4Q²-1)½Imax.=2Q²/ (4Q²-1))½Imax.

microscope

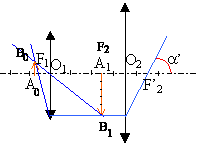
Lobjectif et l'oculaire d'un microscope peuvent être assimilés à deux lentilles minces convergentes L1 et L2.  Le foyer image F'1 de l'objectif L1 et le foyer objet F2 de l'oculaire L2 sont distant de D. On désigne par f'1 et f'2 les distances focales respectives de L1 et L2. Un observateur dont l'oeil est normal et accommode à l'infini, regarde un objet A0B0 à travers l'instrument.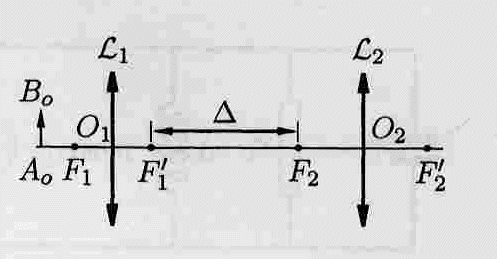

  1. Calculer p0 = O1A0 pour qu'une image nette se forme sur la rétine.( ce qui écrit est en bleu et en gras est algébrique)
  2. Calculer le grandissement transversal gob de l'objectif.
  3. On désigne par dm la distance minimale de vision distincte d'un oeil normal. On définit le grossissement commercial G d'un instrument d'optique par le rapport G= ai / a 0 où ai est l'angle sous lequel un oeil normal accommodant à l'infini voit l'objet à travers l'instrument et a0 l'angle sous lequel l'objet est vu de l'oeil nu lorsqu'il est placé à la distance dm.
    - Déterminer le grossissement commercial de l'oculaire Goc en fonction de f'2 et dm.
  4. Exprimer le grossissement commercial Gm du microscope en fonction de Goc, D et f'1.
  5. On définit la puissance P du microscope par le rapport P= a' / A0B0 de la dimension angulaire a' de lobjet vu à travers l'instrument par un oeil normal accommodant à l'infini sur la dimension A0B0 de l'objet. Calculer P.
  6. On appelle cercle oculaire l'image que donne le microscope de la monture de l'objectif. En considérant un objet placé dans le plan de front passant par O1, exprimer à quelle distance d1 de O2 se trouve le cercle oculaire.
  7. La monture de l'objectif est constituée par un diaphragmme de diamètre D. Exprimer le diamètre d de l'oculaire.
corrigé
La lentille L1 donne de l'objet A0B0 une image A1B1 qui se forme en F2. A1B1 sert d'objet pour l'oculaire. L'image définitive se forme à l'infini, l'objet A1B1 étant au foyer objet de l'oculaire.

Relation de conjugaison pour l'objectif L1 : 1/f'1 = 1/ O1A1-1/p0 ;

1/p0 = 1/ O1A1- 1/f'1 avec O1A1= D + f'1 ;

1/p0 = 1/( D + f'1) - 1/f'1 = -D / (( D + f'1)f'1)) ; p0 = -( D + f'1)f'1 / D .

grandissement transversal gob = A1B1 / A0B0 =O1A1/ p0 = -D / f'1.

tan ai = A0 B0 / O2F2 = A0 B0 /f'2.

tan ai proche de ai si l'angle est petit : ai = A0 B0 /f'2.

l'angle étant petit on peut confondre l'angle en radian avec sa tangente :

a0 voisin tan a0 = A0B0 / dm .

grossissement Goc = dm / f'2.grossissement commercial Gm du microscope = Goc gob= - Goc D / f'1.

puissance P du microscope P= a' / A0B0.

tan a' = A1 B1 / O2F2 = A1 B1 / f'2.

tan a' proche de a' soit a' = A1 B1 / f'2.

l'angle étant petit on peut confondre l'angle en radian avec sa tangente :

A1 B1 / A0B0= O1 F2/ O1 A0 avec O1 F2= f'1+D et O1 A0= -( D + f'1)f'1 / D .

P= a' / A0B0 = - D / (f'1f'2)

cercle oculaire l'image que donne le microscope de la monture de l'objectif.

relation de conjugaison appliquée à L2 :

1/f'2 = 1/ d1 -1/O2O1 ;

1/d1 = 1/ O2O1 + 1/f'2 avec O2O1 = -( D + f'1+f'2)

1/d1 = -1/( D + f'1+f'2) + 1/f'2 = (D+ f'1) / (( D + f'1+f'2)f'2)) ; d1 = ( D + f'1+f'2)f'2) / (D+ f'1) .

diamètre d du cercle oculaire :

grandissement transversal de l'oculaire : |g|= d/D= d1/ ( D + f'1+f'2)= f'2 / (D+ f'1)

d= D f'2 / (D+ f'1)

densitomètre

Un densitomètre est constitué d'un tube cylindrique (T) de masse m=10 g, de hauteur H= 30 cm et de section S= 1 cm² lesté dans sa partie inférieure par un réservoir sphérique (R) de rayon R, de volume V0 = 1 cm3 dont la masse et l'épaisseur des parois sont négligeables. Le réservoir est rempli dans la totalité du volume V0 de mercure ( rHg= 13,6 g/cm3). Le densitomètre est plongé dans un liquide de masse volumique r et l'on désigne par h la hauteur immergée du tube cylindrique T.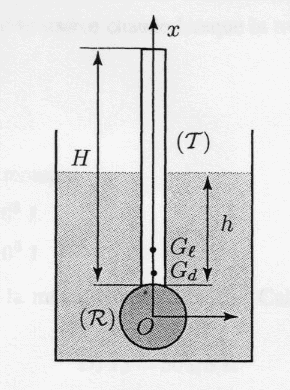

  1. Calculer la position xd= OGd du centre de masse du densitomètre par rapport au centre de masse O du lest.
  2. Exprimer la position xl= OGl du centre de masse Gl du liquide déplacé par le densitomètre par rapport au centre de masse O du lest en fonction de S, V0, R et h.
  3. Montrer que le densitomètre conserve une position d'équilibre stable, tige verticale, si h vérifie l'inéquation h²-2bh-c>0. Donner la valeur numérique de b.
  4. Calculer c.
  5. Calculer la hauteur minimale hm que doit avoir h pour que le densitomètre reste en équilibre stable, tige verticale.
  6. Calculer la valeur minimale rm de la masse volumique r du liquide que l'on peut mesurer avec ce densitomètre.
  7. Calculer la valeur maximale rM de la masse volumique r du liquide que l'on peut mesurer avec ce densitomètre si l'on veut que sa tige reste naturellement verticale pendant la mesure.
 
corrigé
centre de masse du lest : O ; masse du lest : m2 = V0 rHg= 13,6 g ;

rayon du lest sphérique : 4/3 p R3 = 1 ; R= 0,62 cm = 6,2 10-3 m.

Le centre de masse du tube seul est situé en C, à mi-hauteur, soit à 0,15 m du bord inférieur du tube T ;

masse du tube m1 = 0,01 kg

m2 OGd = m1 GdC1 avec OGd + GdC1 = 0,15 + 6,2 10-3 = 0,1562 m

0,0136 OGd = 0,01(0,1562-OGd) ; OGd = 0,0662 m.

centre de masse du lest : O ; masse du liquide déplacé par la sphère : m3 = V0 rl ;

Le centre de masse du liquide déplacé par le tube immergé, noté C2, est situé à mi-hauteur ½h

masse du liquide déplacé par le tube immergé : m4 = Sh rl ;

m3 OGl = m4 GlC2 avec OGl + GlC2 = R+½h

V0 rl OGl = Sh rl ( R+½h-OGl) ; OGl = ( R+½h) Sh / (V0 + Sh).

Le densitomètre reste stable tant que Gd est en dessous de Gl : OGd <OGl .

0,0662<( R+½h) Sh / (V0 + Sh)

0,0662(V0 + Sh) - ( R+½h) Sh<0

-½Sh² +(0,0662-R)Sh + 0,0662 V0<0

½Sh² -(0,0662-R)Sh - 0,0662 V0>0

h² -2(0,0662-R)h- 0,0662*2 V0/S>0

b= 0,0662-R = 0,0662-6,2 10-3=0,06 m.

c = 0,0662*2 10-6/10-4 = 1,32 10-3 m².

hauteur minimale hm : le point Gl vient en Gd ;

h² -0,12 h-1,32 10-3 =0

résoudre : hm=13,01 cm.

valeur minimale rm de la masse volumique r du liquide que l'on peut mesurer avec ce densitomètre :

la tige est totalement immergée : h = 0,3 m

le poids du densitomètre est égal à la poussée d'Archimède due au liquide déplacé

(10 + 13,6) 10-3 g = (V0+Sh)rlm g

rl m=23,6 10-3 / (V0+Sh) = 23,6 10-3 / (10-6+10-4*0,3) =761 kg m-3

valeur maximale rM de la masse volumique r du liquide que l'on peut mesurer avec ce densitomètre :

le point Gl vient en Gd : h = 0,13 m

le poids du densitomètre est égal à la poussée d'Archimède due au liquide déplacé

(10 + 13,6) 10-3 g = (V0+Sh)rlm g

rl m=23,6 10-3 / (V0+Sh) = 23,6 10-3 / (10-6+10-4*0,13) =1686 kg m-3


moteur thermique

Un moteur thermique fonctionne de façon réversible entre deux sources dont les températures Tc et Tf (Tc > Tf) peuvent évoluer au cours du temps à cause des échanges thermiques avec la machine. La source froide est constituée d'une masse M = 100 kg d'eau en totalité à l'état de glace fondante à la température Tf0= 273 K. la source chaude est constituée par une masse 2M d'eau liquide à la température Tc0 = 373 K. On donne :

capacité thermique massique de l'eau liquide C= 4,18 kJ kg-1 K-1.

chaleur latente massique de fusion de la glace à 273 K : L= 335 kJ/kg.

  1. Déduire d'un bilan entropique effectué sur la machine, la température Tcl de la source chaude lorsque la totalité de la glace de la source froide a fondu.
  2. Calculer dans ce cas le travail W1 fourni par le moteur.
  3. Le moteur s'arrête de fonctionner lorsque les deux sources sont à la même température T0. Calculer T0.
  4. Calculer le travail total W2 fourni par le moteur depuis le début de son fonctionnement jusqu'à ce qu'il s'arrête.
  5. Calculer le rendement thermique global h du moteur.
  6. Calculer le rendement thermique global h0 du moteur si on avait maintenu constante les températures initiales des deux sources
 
corrigé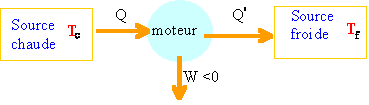

lors d'un cycle et un fonctionnement réversible:

premier principe : dQ+dQ'+dW=0

second principe :

avec dQ = 2MC dT et dQ' = MC dT' (lorsque toute la glace a fondu)

et dQ' = L d m ( lorsque la masse d m de glace a fondu ; d m<M)

2MC dT / T + L d m / Tf0=0 puis intégrer entre 0 et M.

C ln(Tcl/Tc) + ½L / Tf0=0 ; ln(Tcl/Tc) = -½L / (Tf0C)

ln(Tcl/373) = -0,5*335 /(273*4,18)= -0,147

Tcl/373 = 0,863 ; Tcl=0,863*373 = 322 K.

 travail fourni W1 par le moteur : W1+Q+Q'=0

avec Qreçu = 2MC(Tc-Tcl)= 200*4,18(373-322)= 42 636 kJ

Q' cédée= -ML= -100*335 = -33 500 kJ

W1fourni = - 42636+33500 = -9 116 kJ.

2MCdT / T + MCdT' / T' =0 ( lorsque la glace a fondu)

2dT / T + dT' / T' =0

puis intégrer sur la durée du fonctionnement ( glace fondue)

2 ln( T0/ Tcl) +ln( T0 / Tf) =0

T03 = Tf T²cl.

T0 = racine cubique (273* 322² )= 304,7 K.

Le moteur cesse de fonctionner lorsque les 2 sources sont à la même température.

travail du moteur lors de cette seconde phase :

Qreçu = 2MC(Tcl-T0)= 200*4,18(322-304,7)= 14 462,8 kJ

Q' cédée= -MC(T0-Tf)= -100*4,18(304,7-273) = -13 250 kJ

W2fourni = + 13 250 - 14 462,8 = -1 212,2 kJ.

total : -1 212,2 - 9 116 = -10 328,2 kJ.

rendement thermique global h du moteur :

conversion en travail de l'énergie thermique reçue = 10328,2 / (14 462,8+ 42 636) = 0,18.

rendement théorique maxi , dans le cas où les températures des sources restent constantes

1-Tf/Tc = 1 -273 / 373 = 0,27.


réseau électrique

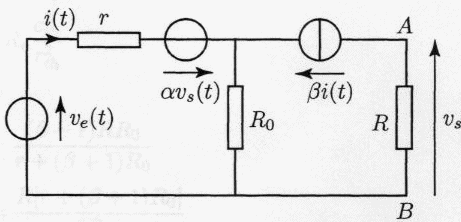
La source qui délivre la tension d'entrée vE(t) = VEcos(wt) est un générateur parfait autonome.  Les deux autres générateurs, parfaits eux aussi, sont des sources liées, commandées respectivement par la tension de sortie vS(t)= vA-vB pour la source de tension et pour la source de courant, par le courant i(t)= I0cos(wt) délivré par la source autonome. a et b sont des constantes.

Du point de vue de ces bornes de sortie A et B, ce réseau dans lequel est compris le résistor R connecté entre les bornes A et B, est équivalent à un générateur qui, dans la représentation de Thévenin, est constitué par une source de tension de force électromotrice eth(t) associé en série à un résistor rth.

Dans la représentation de Norton, ce générateur est constitué d'une source de courant, de courant électromoteur iN(t), associée en parallèle à un résistor de résistance Rth.

  1. Exprimer la résistance d'entrée Re du circuit définie par le rapport Re= ve(t) / i(t).
  2. Calculer eth.
  3. Calculer rth
  4. Calculer iN
  5. Calculer Rth.
  6. Un résistor de résistance Ra est connecté entre les bornes A et B, en parallèle sur le résistor de résistance R. Exprimer en fonction de Ra et des caractéristiques du générateur équivalent, la puissance moyenne Pa calculée sur une prériode dissipée dans Ra, sachant que l'amplitude ve de la tension d'entrée s'exprime en volt efficace.
  7. Pour quelle valeur de Ra cette puissance est-elle maximale ?
corrigé
La tension aux bornes du résistor R0 est notée u ; il est traversé par un courant d'intensité (b+1) i : u = R0(b+1) i

de plus vs= Rbi ; maille de gauche : u = ve-ri-avs.

R0(b+1) i = ve-ri-aRbi

[R0(b+1) + r + aRb] i = ve ; Re = ve / i = R0(b+1) + r + aRb.

eth = uAB= vs = Rbi avec i = ve /Re.

eth = Rbve /Re.

on court circuite R : le courant de court circuit iN est éagl à : iN = b i avec i = ve /Re.

iN = b ve /Re.

rth = Rth = eth / iN = R.

puissance moyenne Pa calculée sur une période dissipée dans Ra:

L'ensemble du circuit est équivalent à un générateur parfait de tension de fem eth en série avec les résistors de résistance rth et Ra. L'intensité du courant qui traverse Ra est : eth/(rth+Ra). La tension aux bornes de Ra est : Ra eth/(rth+Ra)

d'où Pa = Ra e²th/(rth+Ra)².

valeur de Ra pour laquelle cette puissance est-elle maximale :

on dérive Pa par rapport à Ra :

Pa' = e²th(rth-Ra)/(rth+Ra)3.

la dérivée s'annule pour Ra0 = rth ; la dérivée est négative si Ra0 > rth : Pa passe par un maximum si Ra0 = rth.

retour -menu