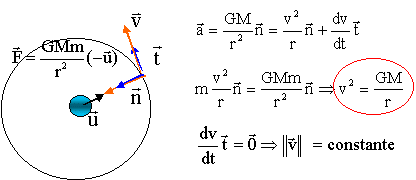|
culture générale - sons - dipôle
(RL) -circuit RC et moteur
- esterification- gravitation - radioactivité- dipole
LC ; métronome
|
||||||||||||||||||||
|
|
||||||||||||||||||||
|
||||||||||||||||||||
|
|
corrigé 1000 kg/m3 ( le corps est composé essentiellement d'eau) phase : rouge ; neutre : bleu ; fil de terre : jaune et vert tension efficace entre la phase et le neutre : 230 V tension efficace entre le neutre et la terre : 0 V gaz à effet de serre : CO2 et méthane ou encore NO2. La pousséed' Archimède est une force verticale et ascendante dont la norme est égale au poids du fluide déplacé. projet international ITER concernant la fusion nucléaire : France Japon bronze, laiton, quartz, Aluminium ne contiennent pas l'élément carbone
|
|||||||||||||||||||
|
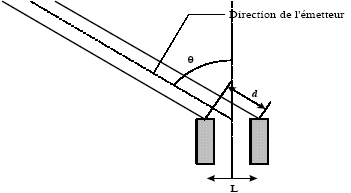
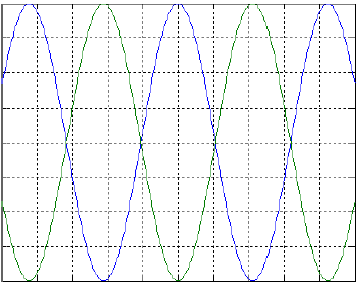
sujet 2 Un émetteur émet des ondes acoustiques de façon continue. Deux récepteurs, disposés sur le trajet des ondes et distants de D = 36 mm, permettent d’enregistrer le signal émis et de le visualiser sur l’écran d’un oscilloscope. Le dispositif expérimental est schématisé ci-dessous. 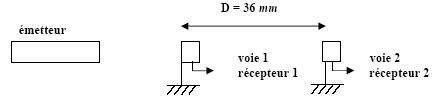 On observe à l’oscilloscope le signal reçu par le récepteur 1 ; il est reproduit ci-dessous, la vitesse de balayage Vb étant de 50 µs / div : 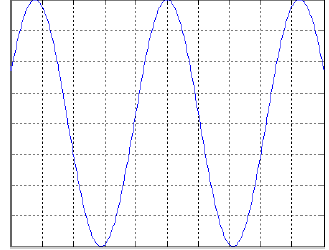 On rappelle que la célérité des ondes acoustiques dans l’air dans les conditions atmosphériques moyennes est c = 340 m.s-1.
corrigé période: 4,3 divisions soit 4,3*5010-6 = 2,15 10-4 s ; fréquence f= 1/ 2,15 10-4 = 4,65 kHz, sons aigus longueur d'onde l = c/ f = 340/4650 = 7,3 10-2 m = 7,3 cm. la distance des deux récepteurs est très proche d'une demi-longueur d'onde, en conséquence les récepteurs sont en opposition de phase.
si l’on ajoute les deux signaux reçus par les deux détecteurs on obtient un signal d'amplitude nulle. différence de trajet d entre les signaux reçus par les deux détecteurs d = L sin q. la somme des deux signaux est nulle si d est un multiple impaire de la demi longueur d'onde : d = L sin q = ½(2k+1)l. si k= 1 alors sin q = l /(2L) = 73 / ( 2*60) =0,608 et q =0,65 rad.
|
||||||||||||||||||||
|
sujet 3 : On utilise le montage ci-dessous comportant une résistance R, un condensateur déchargé C et un moteur M. Cemoteur peut entraîner une poulie permettant de soulever, à l’aide d’un fil, une masse m sur une hauteur h. 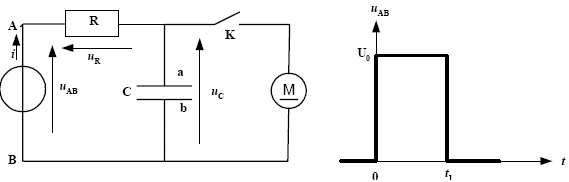 L’interrupteur K étant ouvert, on applique entre les bornes A et B la tension uAB dont l’évolution en créneau de durée t1, est représentée en fonction du temps. Données : R = 1 k.W ; C = 1000 µF et U0 = 12 V.
corrigé courbe III : pendant la charge, la tension uc aux bornes du condensateur croît jusqu'à la valeur U0= 12 V courbe V : pendant la charge, la tension uR aux bornes de la résistance décroît( comme l'intensité )de la valeur U0=12 V jusqu'à la valeur nulle. courbe V : pendant la charge, l'intensité du courant i dans le circuit décroît de la valeur U0/R = 12 / 1000 = 12 mA à zéro. la constante de temps t de ce circuit : t = RC = 1000 * 10-3 = 1 s. la plus faible valeur de durée t1 du créneau permettant à la tension uc d’atteindre 99% de la valeur UCM est égale à : uc= U0(1-exp(-t/t)) ; 0,99 U0 =U0(1-exp(- t1/t)) ; 0,99 =1-exp(- t1/t) ;exp(- t1/t) = 0,01 - t1/t = ln 0,01 = -4,61 soit t1 = 4,61 t = 4,61 s.
t1 = 100 s le condensateur est chargé ; la tension à ses bornes vaut 12 V ; C= 10-3 F qa= CU0 = 12 10-3 C ; qb= -qa = - 12 10-3 C ; énergie stockée dans le condensateur : ECE =½q²a/C= 0,5*(12 10-3)2/10-3 = 72 10-3 J. ECA restant emmagasinée dans le condensateur : ½CU²= 0,5*10-3*4,8²= 11,5 10-3 J l’énergie ECF fournie par le condensateur au moteur :(72-11,5)10-3 = 60,5 10-3 J. l’énergie EM communiquée par le moteur à la charge
: mgh = 0,01*10*0,35 = 35 10-3 J.
|
||||||||||||||||||||
|
sujet 4 On se propose d’étudier la réaction de formation de l’ester de formule semi-développée : HCOOCH2(CH2)2CH3 Pour ce faire, on réalise à l’instant t = 0 un mélange
équimolaire d’un acide carboxylique AH et d’un alcool noté ROH ; ce
mélange est porté à reflux. Toutes les 10 minutes, on prélève 5% (soit
1/20ème) du milieu réactionnel. Ce prélèvement est ensuite dosé par une
solution molaire d’hydroxyde de sodium (NaOH) selon le protocole
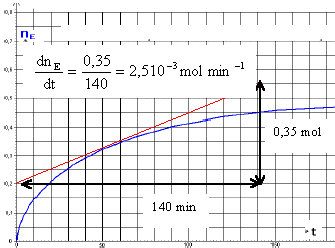
suivant : b) ajout de 3 gouttes d’indicateur coloré c) dosage au moyen d’une burette par une solution aqueuse : [NaOH] = 1 mol.L-1. La réaction de dosage est instantanée et peut être considérée comme totale : AH + OH- --> A- + H2O Le résultat de ces analyses permet de tracer la courbe donnant l’évolution de la quantité totale d’acide au cours de la réaction : 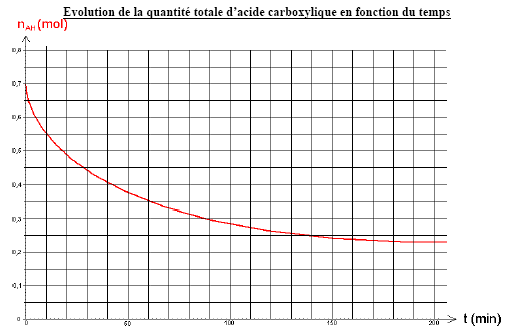
corrigé HCOO H + HOCH2(CH2)2CH3= HCOOCH2(CH2)2CH3 + H2O. nom de l'ester : méthanoate de n-butyle. mase molaire de l'ester C5H10 O2 : M= 12*5+10+2*16=102 g/mol nE = n0 (acide) - n acide (t) = 0,7 - n acide (t)
constante d’équilibre de la réaction de dosage : AH + HO- = A- + H2O ; K= [A-]/([AH][HO-]) avec Ka = [A-][H3O+]/([AH]= 10-3,8 ; K= [A-][H3O+]/([AH][HO-][H3O+]) = Ka / Ke = 10-3,8 / 10-14 = 1010,2 = 1,6 1010. volume équivalent de soude versé pour le sixième dosage : d'après le graphe il reste 0,35 mol d'acide soit dans le prélèvement : 0,35/20 = 1,75 10-2 mol à l'équivalence du dosage acide base : 1,75 10-2 = Cb Vbe d'où Vbe = 1,75 10-2 / Cb= 1,75 10-2 / 1 = 1,75 10-2 L. rendement = nester formé / n ester théorique = (0,7-0,23)/0,7 = 0,47/0,7 = 0,67 ( 67 %) valeurs obtenues sur le graphe. augmenter la vitesse sans modifier le rendement final par rapport à l’acide : augmenter la température ou utiliser un catalyseur.
|
||||||||||||||||||||
|
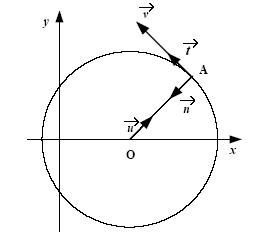
sujet 5 La Terre peut être considérée comme un corps à symétrie sphérique de centre O de rayon R et de masse M. Soit un objet ponctuel de masse m, situé en A distant de r du centre de la Terre. G : constante de gravitation. .u : vecteur unitaire dirigé de O vers A. F: force d’attraction gravitationnelle appliquée à l’objet de masse m. 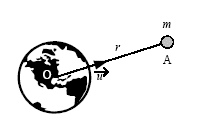
corrigé Le poids est à peu près égal à la force de gravitation mg= GMterre m / r² d'où g= GMterre / r² à la surface de la terre r= Rterre. g0 = GMterre / R²terre
période T de rotation autour de la Terre en fonction de r : La période est la durée pour pacourir une circonférence de rayon r à la vitesse v 2pr = vT 4p²r² = v²T² = GMT² / r T² = r3 4p²/ (GM) ; T= 2p [r3/ (GM)]½. La Terre doit faire plus d’un tour, autour d’elle-même pour que le Soleil reviennent au zénith. En un an, la Terre aura fait 366,25 tours sur elle-même par rapport à un repère Galiléen. T² = r3 4p²/ (GM) ; r3 = T² GM / (4p²) avec GM= g0R² r3 = T² g0R²/ (4p²) = 86164²*9,81*(6,38 106)²/ (4*3,14²)= 7,52 1022 ; r = 4,22 107 m z= r-R= 4,22 107 =6,38 106 =3,58 107 m.
|
||||||||||||||||||||
|
sujet 6
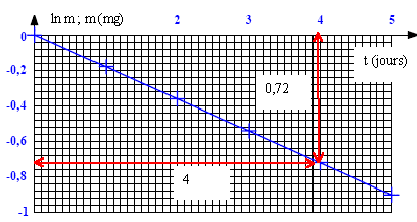
corrigé AZX= 42He + A-4Z-2Y : émission a AZX= 0-1e + AZ+1Y : émission ß- 22286Rn fait partie d’une famille radioactive qui, par une série d’émissions ß- et a, aboutit au plomb 20682Pb : le nombre de nucléons diminue de 222-206 = 16 : donc 4 désintégrations de type a le nombre de charge diminue globalement de 4 : donc 4 désintégrations de type ß-. demi-vie : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrés ; la masse initiale du radon est alors divisée par 2. D'après les données du tableau, l’ordre de grandeur de la demi-vie du radon 222 est un peu inférieure à 4 jours.
coefficient directeur = -0,72 / 4 = -0,18 jour-1. de plus m= m0 exp(-lt) ; ln m = ln m0 -lt donc droite de coefficient directeur -l : l=0,18 jour-1. demi vie t½ : t½l=
ln2 soit t½= ln2 / l= 0,693 / 0,18 = 3,85 jours.
N0 = 10-3 /222*6,02 1023 = 2,71 1018 noyaux de radon 222. l=0,18 jour-1 = 0,18/(24*3600) s-1= 2,08 10-6 s-1. A0 = N0 l = 2,71 1018*2,08 10-6 = 5,64 1012 Bq. masse m10 et l’activité A10 de l’échantillon de radon à t = 10 jours : A10 = A0exp(-lt) =5,64 1012 exp(-0,18*10)= 9,32 1011 Bq. m10 = m0exp(-lt) =1 exp(-0,18*10)= 0,16 mg.
|
||||||||||||||||||||
|
sujet 7 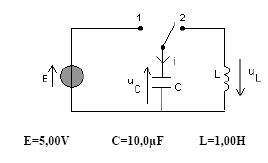 On néglige la résistance interne de la bobine. Initialement l’interrupteur est en position 1 depuis un temps très long. A t = 0, on bascule l’interrupteur de la position 1 vers la position 2. Dans tout l’exercice, on considérera que l’interrupteur a déjà basculé.
or q= Cuc ; i = dq/dt = Cduc/dt ; di
/dt= d²q/dt² = Cd²uc/dt ² = Cu"c équation différentielle à laquelle obéit uc : uc + LCu"c = 0 ou bien u"c + 1/(LC) uc=0 expression de la fréquence propre en Hz : f= 1/(2p(LC)½)= 1/(6,28 (10-5)½=50,3 Hz. expression littérale du courant i en fonction du temps : uc= U0 cos ( 2pf t+j) i = Cduc/dt = -CU02pf
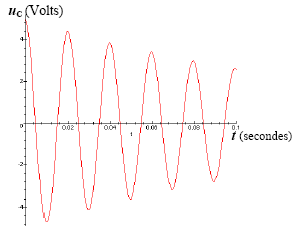
sin ( 2pf t+j) Analyse de la courbe uc(t) : ce modèle ne convient pas : il implique la présence de résistor dans le dipole (LC), responsable de l'amortissement.
|
||||||||||||||||||||
|
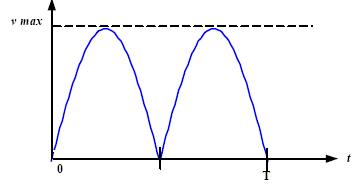
sujet 8 On considère un métronome que l’on modélise par un pendule de longueur réglable L = OA. Il est constitué par une masse considérée comme ponctuelle M = 20 g placée au bout d’une tige rigide de masse négligeable. Les frottements seront négligés. 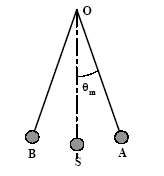 Quand on écarte le pendule de sa position d’équilibre verticale d’un angle q m, il oscille dans un plan vertical, la masse M oscillant entre les positions limites A et B. On appelle q (t) l’angle que fait la tige avec la verticale à l’instant t. A l’instant t = 0, on écarte le pendule d’un angle q m = 8° et on le libère sans vitesse initiale. Lorsque la masse M passe en A et en B, le métronome émet un signal sonore. On choisit comme origine des énergies potentielles le plan horizontal passant par la position de la masse M au repos (point S). Le métronome est placé dans un laboratoire où g = 9,81 m.s-2.
corrigé période des oscillations du pendule simple T = 1 s. T=2p(L/g)½ ; longueur L = T²g/(4p²)= 1*9,81/(4*3,14²)= 0,249 m. q(t) = a cos (b t + c). 8 degrés = 0,14 rad. ; a= 0,14 rad. b = pulsation = w = 2pf= 2p/T= 6,28 rad/s. c: phase à l'origine = 0. q ' = -ab sin (bt+c) la vitesse en A est nulle ; la vitesse est maximale en S. vS= L q '(t= T/4) =0,249*0,14*6,28 sin(½p) = 0,22 m/s.
énergie potentielle Ep au point A : Ep= mgL(1-cos q m )= 0,02*9,81*0,249(1-cos 8)=4,8 10-4 J l'énergie cinétique Ec du pendule au point A est nulle. l’énergie mécanique EM se conserve : au point S l'énergie mécanique est égale à l'énergie potentielle au point A. accélération de pesanteur gL sur la Lune : TL=2p(L/g)½ ; gL = 4p²L /T²L= 4*3,14²*0,249/ 2,45²= 1,64 ms-2.
|
||||||||||||||||||||
|
|
||||||||||||||||||||
|
|