Aurélie 04/05

mécanique ;

circuit RC ; niveau d'énergie ; radioactivité ; onde

physique : 2 h ; 5 exercices à traiter ; d'après concours Ecole Polytechnique Féminine 2004




Google



Mécanique ( obligatoire)

Dans cet exercice un objet de masse m et de centre de gravité G est en mouvement dans un référentiel galiléeen terrestre. On note.F la somme des forces appliquéees à ce solide, v son vecteur vitesse et a son vecteur accélération.

  1. Enoncer la relation fondamentale de la dynamique (ou seconde loi de Newton).
  2. Les situations suivantes sont-elles possibles ? Justifier.

corrigé
Dans un référentiel galiléen, pour un objet ponctuel (de petites dimensions ), de masse m, la somme des

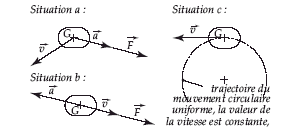
forces extérieures appliquées à cet objet est égale au produit de sa masse par l' accélération de son son centre de gravité.

situation a : possible car la force est colinéaire et de même sens que l’accélération.

situation b : impossible, l’accélération et la force sont colinéaires et de sens contraire ce qui conduirait à une masse "négative".

situation c : impossible, la force est nulle ; pour avoir un mouvement circulaire uniforme, la force doit être centripète ( exemple force de gravitation).

circuit oscillant : obligatoire

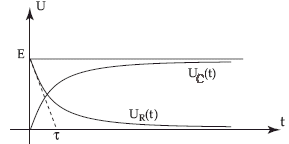
On consid`ere un dipôle R, C série, alimenté par un générateur idéal délivrant une tension e(t). A t = 0 s, on ferme l’interrupteur K.

  1. Ecrire l’équation diff´erentielle reliant q, dq dt et e.
  2. La tension e(t) étant désormais continue (et valant E), montrer que l’équation différentielle admet comme solution q(t) = CE(1-exp(-t/(RC)) en supposant le condensateur initialement déchargé.
  3. Trouver les tensions uR(t) et uC(t). Tracer ces deux évolutions sur un même graphique (système d’axes (O, t, u(t))).
  4. Quelle est la constante de temps ? A quoi correspond-elle sur le graphique ?
 

corrigé
uR(t) + uC(t) = e(t) ; avec uR(t) = R i(t) , uC(t) = q(t) / C et i(t) = dq(t) / dt soit

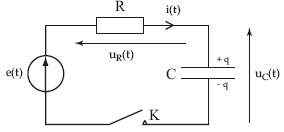
R i(t) + q(t) / C = e(t) soit R dq(t) / dt + q(t) / C = e(t)

q' + 1/(RC) q= E on pose t = RC, constante de temps du dipôle

q' + 1/t q= E/R.(1)

q(t) = CE(1-exp(-t/t) ; q'(t) = CE / t exp(-t/t) = CE /(RC) exp(-t/t) = E/Rexp(-t/t)

repport dans (1) : E/Rexp(-t/t) + CE / (RC)(1-exp(-t/t)= E

E/Rexp(-t/t) +E/R - E/Rexp(-t/t) = E/R, vérifié quel que soit t.

uR(t) = Ri(t) = R dq(t) / dt = E exp(-t/t)

uC(t) = q(t) / C = E(1-exp(-t/t)

t est obtenu en traçant la tangente à l'origine à l'une des courbes ; puis en recherchant l'abscisse du point d'intersection de cette tangente avec l'asymptote horizontale.

niveau d'énergie :obligatoire

Supposons qu’une planète rayonne de la lumière ultraviolette aux travers d’une atmosphère gazeuse comportant une majorité d’atome d’hydrogène. Les longueurs d’onde du rayonnement sont inférieures à 91,2 nm.

Données : Constante de Plank h = 6, 62×10-34 J.s. Célérité des ondes électromagnétiques c = 3×105 km.s-1.

Charge élémentaire e = 1, 6 × 10-19 C.

  1. Donner la signification du niveau d’énergie E = 0 eV
  2. Quel est le niveau d’énergie d’un atome d’hydrogène pris dans son état fondamental lorsqu’il subit une radiation de 91, 2 nm ? Exprimer l’énergie en Joule et en eV .
  3. Expliquer ce qui se passe lorsqu’un atome d’hydrogène reçoit une radiation de longueur d’onde inférieure à 110 nm.
  4. Quelle est la longueur d’onde émise lorsqu’un atome d’hydrogène passe de l’état excité n = 3 à l’état n = 2.

corrigé
E = 0 correspond à l’état d’excitation maximale ou encore à l'atome ionisé ( perte de son électron)

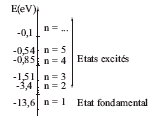
énergie reçue par l'atome : E = hc / l = 6,62 10-34* 3 108 / 91,2 10-9= 2,18 10-18 J

2,18 10-18 / 1,6 10-19 = 13,6 eV

énergie initiale de l'atome pris dans son état fondamental : -13,6 eV

énergie totale de l'atome : 0 eV, après avoir reçu le photon.

un atome d’hydrogène reçoit une radiation de longueur d’onde inférieure à 110 nm

énergie de la radiation : hc / l = 6,62 10-34* 3 108 / 110 10-9= 1,8 10-18 J

1,8 10-18 / 1,6 10-19 = 11,3 eV

l'atome se trouve alors dans l'un de ces état excités si le photon est absorbé ( l'énergie du photon doit être égale à la différence d'énergie entre deux niveaux de l'atome)

si la longueur d'onde est inférieure à 91,2 nm, l'atome est ionisé.

Variation d’´energie : E=13,6 ( 1/4-1/9)= 1,89 eV soit 1,89*1,6 10-19= 3,024 10-19 J.

La longueur de l’onde émise est donc : l = hc/E

l = 6,62 10-34* 3 108 /3,024 10-19 = 657 10-9 m.


radioactivité ( au choix)

Le césium 13755Cs constitue une source radioactive, il est émetteur ß- et donne un noyau de baryum qui subit ensuite une désexcitation.

  1. Ecrire l’équation-bilan de la désintégration ß- du césium.
    - Ecrire l’équation-bilan de la désexcitation du baryum. Préciser le nom du rayonnement émis lors de la désexcitation. Cette d´esexcitation modifie-t-elle le numéro atomique et le nombre de masse du baryum ?
    - Le temps de vie du césium 137 est de 30 ans et son activité initiale lors de sa préparation est A0 = 3, 0 × 104 Bq. Quelle est l’activité de la source 5 ans après sa préparation ?
  2. On effectue une série de mesures à l’aide du compteur Geiger-Muller. La durée de chaque comptage est de 1 s et on effectue 100 comptages. On note n le nombre d’impulsions détectées par comptage et f le nombre de fois où la valeur n a été mesurée.

    - Pourquoi le nombre d’impulsions détectées par seconde est-il très inférieur à l’activitè de la source ?
    - L’histogramme représentant f en fonction de n est représenté ci-dessous : Quelle caractéristique du phénomène de radioactivité cet histogramme met-il en évidence ?
    - La valeur moyenne de n est nmoyen = 13,7 et l’écart type s = 0, 4, par conséquent, nous avons 95% de chance d’avoir 13, 3 < n < 14, 1. Une mesure est effectuée, nous obtenons n = 17. Cette valeur est-elle compatible avec les résultats donnés ci-dessus ?

corrigé
L’équation-bilan de la désintégration ß- du césium est : 137

13755Cs -->13756Ba* + 0-1e

désexcitation du Baryum : 13756Ba* -->13756Ba+ 00g. photon gamma.

Le numéro atomique et nombre de masse ne sont pas modifiés. L’énergie de l'atome diminue : le surplus est emporté par le photon.

A = A0 exp(-l.t) ; avec l t½ = ln2 soit l = ln2/30 = 2,31 10-2 an-1.

à t = 5 ans : A = 3 104 exp( -2,31 10-2*5) = 2,7 104 Bq.

La source émet dans toutes les directions et le compteur Geiger-Muller ne capture qu'ne petite partie des radiations : le nombre d'impulsions détectées est inférieure à l'activité réelle.

Le phénomène mis en évidence est le caractère aléatoire de la radioactivité.

La mesure effectuée est dans la plage des 5 % mais elle n’est pas incompatible avec les données.


ondes ( au choix)

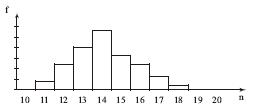
L’observation de la mer à différents moments de la journée permet d’estimer la longueur L entre deux vagues successives et le temps t qui s’écoule entre chaque passage. On obtient les résultats suivants :
L(m)
6,2
16
11
26
t(s)
0,33
0,53
0,45
0,88

  1. Exprimer la célérité V des ondes en fonction de la longueur L et du temps t, puis calculer sa valeur pour les différentes mesures effectuées.
  2. Tracer la courbe donnant la célérité en fonction de la fréquence des vagues. Conclure.
  3. Peut-on dire que les vagues se déplacent ? Quelle est la grandeur qui se déplace ?
  4. Lorsque le vent souffle sur la mer, il se forme des vagues de longueurs différentes. Que peut-on dire de la célérité de ces ondes ? Quelles sont les plus rapides ?
  5. Un enregistrement d’une vague donne le graphique suivant : une étude mathématique de ce signal nous permet de décomposer la vague en vagues élémentaires sinusoïdales dont les paramètres sont donnés ci-dessous.
    - Quelles sont les célérités de ces deux vagues élémentaires ?
    - Que pouvez-vous en déduire sur la forme de la vague au bout d’un certain temps ?

corrigé
célérité V (m/s) = L(m) / t(s) ; fréquence : f (Hz) = V(m/s) /L(m)

L(m)
6,2
16
11
26
t(s)
0,33
0,53
0,45
0,88
V= L / t (m/s)
18,2
30,2
24,5
29,5
f= V/L (Hz)
3
1,9
2,2
1,13

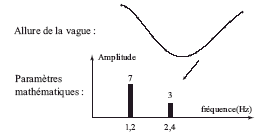
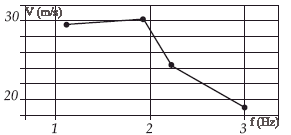
Les ondes qui se propagent sont dispersives : la célérité dépend de la fréquence.

Il n’y a pas de transport de matière, seule l’information et l’énergie sont transportés.

Les célérités de ces ondes sont différentes. Les plus rapides sont celles qui ont les plus grandes longueurs d’onde.

On peut lire sur le graphe : V1 = 30 m/s et V2 = 23 m/s.

La forme des vagues évolue au cours du temps.

dipôle RC ( au choix)

 

  1. Le commutateur est en position 1 depuis très longtemps. Précisez les adjectifs qualifiant le régime. Quelles sont les valeurs littérales de uC, i, uR1 , uR2 et uS ?
  2. A t = 0 s, le commutateur K est placé en position 2. En utilisant les résultats de la question1, que valent, au tout début du régime transitoire q(t = 0+) et uC(t = O+) ? En déduire les valeurs de i(t = 0+), uR1(t = 0+) et uR2(t = 0+).
  3. Ecrire l’équation différentielle régissant q(t) entre t = 0+ et t infini. La résoudre et tracer uR1(t) et uC(t).
  4. Interpréter les valeurs mathématiques trouvées, pour t infini, pour i(t), uR1(t) et uC(t).
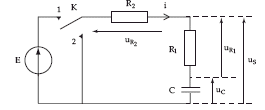
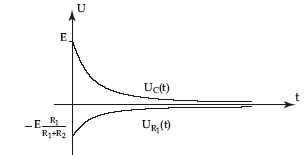
corrigé
En régime est permanent et condensateur chargé : i = 0, uC = E, uR1 =R1 i= uR2 =R2 i= 0 et uS = uC

A t = 0+, le condensateur n'a pas eu le temps de se déchargé: q(t = 0+) = CE et uC(t = O+) = E.

de plus uR1 + uR2 + uC = 0 ; uR1 = R1i et uR2 = R2i. d'où i(t=0+ )= -E/(R1+R2)

uR1(t = 0+) = -ER1 /(R1+R2)

uR2(t = 0+)= -ER2 /(R1+R2)

uR1 + uR2 + uC = 0 donne : (R1+R2) i + q/C=0 avec i = dq/dt = q'

(R1+R2) q' + q/C=0

q' + 1/t q= 0 avect = (R1+R2) C

La solution est de la forme : q(t) =A exp(Bt)

à t=0+ : CE= A ;

i = q' = ABexp(-Bt) ; à t=0+ : -E/(R1+R2) = AB d'où B = - 1/ (R1+R2) C = - 1/t .

uR1(t) =R1 i = -R1-E/(R1+R2) exp(-t / t )

uC(t) = E exp(-t / t ).

Lorsque t tend vers l'infini i tend alors vers 0. Les résistances dissipent l'énergie stockée par le condensateur

uR1(t) tend vers 0

uC(t) tend vers 0 ( condensateur déchargé).

retour -menu