|
l'oeil ; condensateur et dipole RC ; pile cuivre argent ; vitamine C. d'après concours manipulateur électroradiologie médicale Caen 2005 durée 1 h 30 ; |
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||
|
Constante de Plank. h= 6,62 10-34
J s ; charge élémentaire : e= 1,6 10-19 C ;
célérité de la lumière dans le vide c= 3 108 m/s.
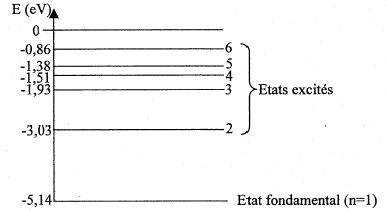
corrigé La discontinuité du spectre prouve que l'énergie de l'atome est quantifiée ; seules, un petit nombre de valeurs sont permises. E= h n = hc/l avec c= 3 108 m/s, l = 589 10-9 m E= 6,62 10-34 *3 108 / 589 10-9 = 3,37 10-19 J puis diviser par 1,6 10-19 pour obtenir l'énergie en électronvolts. E= 2,11 eV. La transition du niveau excité n=2 vers le niveau fondamental s'accompagne de l'émission d'un photon D E=
E(n=2) - E(n=1) = -3,03 - (-5,14) = 2,11 eV
conservation de la charge : 10 = Z-1 soit Z=11 et X est l'élément sodium Na Puis 2311Na* --> 2311Na + 00 g. émission d'un photon gamma, le noyau fils perd de l'énergie et se désexcite Energie du photon g : 4,4-4 = 0,4 MeV = 4 105 eV multiplier par 1,6 10-19 pour passer en joule : 6,4 10-14 J E= h n = hc/l soit l = hc/E= 6,62 10-34 *3 108 /6,4 10-14 =3,1 10-12 m = 3,1 pm.
|
||||||||||||||||||||||||||||||||||
|
Un oeil peut être assimilé à une lentille convergente dans l'air, la rétine jouant le rôle d'écran. L'oeil est loin de travailler dans les conditions de l'approximation de Gauss ; mais la pupille sert de diaphragme et nous appliquerons les formules des lentilles minces. La vergence de la lentille peut être modifiée par les muscles ciliaires qui modifient la forme du cristallin et permettent d'adapter l'oeil à la vision rapprochée : c'est l'accomodation. A. cas de l'oeil "standart ": La distance fixe du cristallin (lentille) à l'écran ( rétine) est de l'ordre de 15,0 mm.
A. cas de l'oeil hypermétrope: l'oeil hypermétrope est trop court. Sa profondeur est par exemple 14,5 mm ; on admettra qu'il possède une vergence minimale de 66,5 dioptries lorsque son cristallin n'accomode pas, et une vergence maximale de 70 duoptries lorsque le cristallin est bombé au maximum.
corrigé Les mesures algébriques sont écrites en bleu et en gras. OA1'= 1,5 10-2 m, image sur la rétine OA1 tend vres l'infini ( objet très éloigné) formule de conjugaison : 1/f'1 = C1 = 1/OA1'-1/OA1 = 1/1,5 10-2 = 66,7 d. OA2'= 1,5 10-2 m, image sur la rétine ( distance cristallin-rétine constante) OA2 = -0,25 m formule de conjugaison : 1/f'2 = C2 = 1/OA2'-1/OA2 = 1/1,5 10-2 -1/(-0,25) = 70,7 d. grandissement transversal g = OA2'/OA2= A2'B2'/A2B2 =1,5 10-2 / (-0,25) = - 6 10-2. A2'B2'=
A2B2
*(-0,06) = 14*(-0,06) = -0,84
cm.
OA'= 1,45 10-2 m, image sur la rétine formule de conjugaison : 1/f' = C = 1/OA'-1/OA soit 1/OA=1/OA' - C = 1/1,45 10-2 - 70,5 = - 1,53 OA= - 0,65 m. oeil + lentille contact : OA = -0,25 m ; OA'= 1,45 10-2 m, image sur la rétine. C "= 1/OA'-1/OA = 1/1,45 10-2 - 1/(-0,25) = 68,96+4= 72,96 d. Clentille = C"-70,5 = 2,46 d. |
||||||||||||||||||||||||||||||||||
|
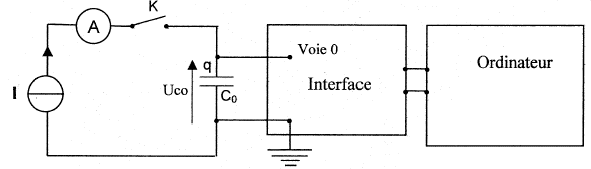
Pour déterminer la capacité d'un condensateur on réalise
la charge à l'aide d'un générateur de courant. Ce générateur débite un
courant d'intensité constante I= 0,50 mA. La saisie automatique de la
tension uc aux bornes du condensateur en
fonction du temps est réalisée avec le montage ci-dessous. On obtient la courbe suivante :
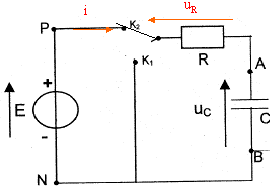
Etude de la charge d'un autre condensateur à travers une résistance R : on utilise un générateur de tension idéeal de fem E. 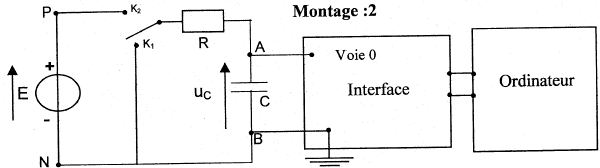 A l'instant initial le condensateur est déchargé et l'interrupteur est basculé en position K2. On enregistre la représentation suivante de uc(t) 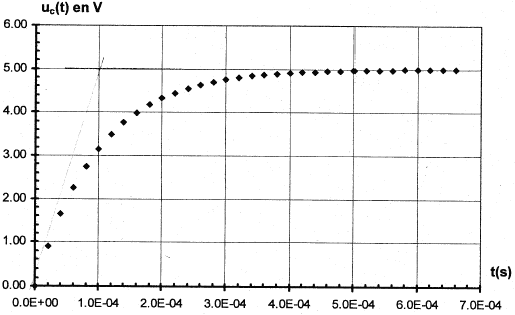
Résolution numérique de l'équation différentielle par la méthode d'Euler : la méthode de résolution numérique permet de trouver des couples de valeur (t ; uc) qui vérifient l'équation différentielle de la relation 1. On rappelle que les couples de valeurs sont liés par la relation uc(ti+1) = uc(ti) + [duc/dt)ti D t avec Dt = 5 10-5 s.
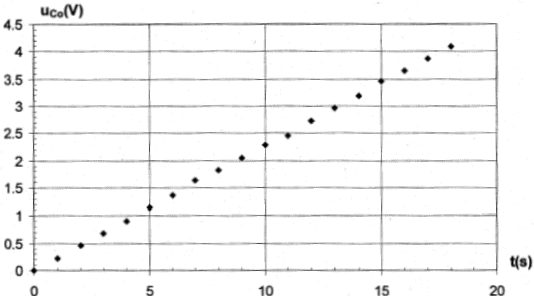
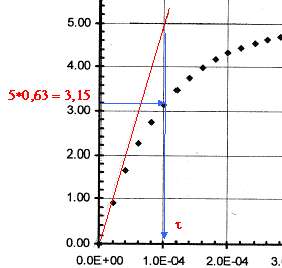
uc=q/C0= I/C0t droite de coefficient directeur I/C0. le coefficient directeur est déterminé graphiquement : 3,5/15 = 0,233 V/s I/C0=0,233 soit C0
= I/0,233 = 5 10-4 / 0,233 = 2,14 10-3
F= 2,14 mF.
RC : V A-1
A s V-1 soit s.
t =
RC= 10-4 s si C= 10-6 F alors R= 100W. ou bien à t =t , uc= 63% de sa valeur maximale. uc+uR= E avec uR= Ri et i = dqA/dt. or Cuc=qA soit i = dqA/dt = C duc/dt = Cuc'. uc+ Ri = E ; uc+ RCuc' = E. au bout d'une durée supérieure à 5t, le condensateur est chargé ; l'intensité est alors nulle, uR=0 et uc= E= 5 V. à t=0+, le condensateur n'a pas eu le temps de se charger et uc=0. uR=Ri0= E ; i0=E/R= 5 /100 = 0,05 A. uc+
RCuc' = E s'écrit : uc' =
1/(RC) (E-uc) = 1/10-4 (
5-uc)= 104( 5-uc)
à t=0 , uc(0)=0 ; [duc/dt)]0=104(5-0)= 5 104 V/s ; à t=5 10-5 s , uc(t1)=uc(0)+ [duc/dt)]0 D t =5 104*5 10-5 = 2,5 V [duc/dt)]t1=104(5-2,5)= 2,5 104 V/s ; à t= 10-4 s , uc(t2)=uc(t1)+ [duc/dt)]t1 D t =2,5+2,5 104*5 10-5 =3,75 V [duc/dt)]t2=104(5-3,75)= 1,25 104 V/s ; à t= 1,5 10-4 s , uc(t3)=uc(t2)+ [duc/dt)]t2 D t =3,75+1,25 104*5 10-5 =4,37 V [duc/dt)]t3=104(5-4,37)= 0,625 104 V/s ;
|
||||||||||||||||||||||||||||||||||
|
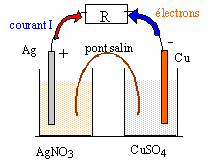
A partir des couples oxydant réducteur Cu2+/Cu(s) et Ag+/Ag(s) on peut envisager deux transformations schématisées par les réactions suivantes : Cu(s) + 2Ag+ = 2 Ag(s)+ Cu2+ (1) constante d'équilibre K1 = 2,1 1015 ; et 2 Ag(s)+ Cu2+= Cu(s) + 2Ag+ (2) K2 A. transformation chimique spontanée par transfert d'électrons : Un élève réalise l'expérience dont le protocole est le suivant : Verser dans un bécher un volume V1 = 50 mL d'une solution de sulfate de cuivre de concentration molaire C1 = 1 mol/L et un volume V2 = 50 mL de solution de nitrate d'argent de concentration molaire C2 = 0,5 mol/L. La solution de cuivre est bleue, celle de nitrate d'argent incolore. Plomnger un fil d'argent et ajouter 3 g de poudre de cuivre rouge. Agiter puis filtrer la solution obtenue et observer la couleur. L'élève note dans les observations de son TP: " on observe un léger dépôt gris et une intensification de la couleur bleue."
B.Constitution et fonctionnement de la pile cuivre argent en circuit fermé : On dispose de fil de cuivre et d'argent, un volume V1 = 50 mL d'une solution de sulfate de cuivre de concentration molaire C1 = 1 mol/L, un volume V2 = 50 mL de solution de nitrate d'argent de concentration molaire C2 = 1 mol/L, un pont salin.
corrigé On observe un dépôt d'argent : 2Ag+ + 2e- = 2Ag(s) la couleur bleue s'intensifie : Cu(s) = Cu2+ + 2e- bilan :2Ag+ +Cu(s) = Cu2+ +2Ag(s) donc réaction (1) [Cu2+]i = V1C1/(V1+V2)=50/100 = 0,5 mol/L ; [Ag+]i =V2C2/(V1+V2)=25/100 = 0,25 mol/L Qr, i = [Cu2+]i /[Ag+]2i =0,5 / 0,252= 8. Qr, i < K, donc évolution
dans le sens direct : les observations sont en accord avec le critère
d'évolution spontané.
2Ag+ + 2e- = 2Ag(s) réduction à la cathode d'argent positive Cu(s) = Cu2+ + 2e-oxydation à l'anode de cuivre négative 2Ag+ +Cu(s) = Cu2+ +2Ag(s)
le numérateur croît, le dénominateur décroît, le quotient de réaction augmente de Qr, i à K1 lorsque la pile fonctionne : Qr diffère de K1,
donc la pile en fonctionnement est un système hors équilibre.
|
||||||||||||||||||||||||||||||||||
|
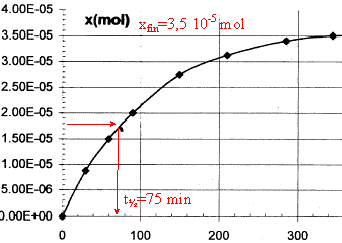
Les trois parties sont indépendantes. La vitamine C est indispensable au bon fonctionnement de l'organisme humain dont elle renforce les défenses immunitaires. Elle doit être apportée par l'alimentation, en particulier les fruits et légumes. Elle est aussi utilisée comme additif alimentaire car elle fait partie de la famille des antioxydants. Réducteur facilement oxydable, elle protège les autres nutriments de l'oxydation. C'est aussi un acide appelé acide ascorbique ( noté AH par la suite) réagissant de façon limitée avec l'eau. A. Dégradation de la vitamine C : la vitamine C se dégrade facilement par oxydation enzymatique aérobie, chauffage, ou exposition à la lumière. La forme oxydée reste néanmoins physiologiquement active. Pour étudier ce phénomène on réalise des titrages à différentes dates d'un volume V= 100 mL d'un jus d'orange ; on obtient la courbe suivante : 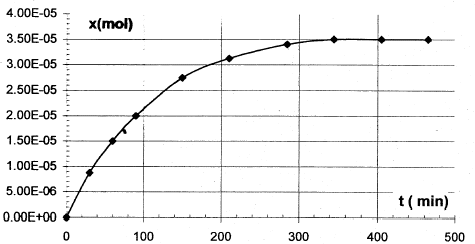
B. réaction entre l'acide ascorbique AH et une solution d'hydroxyde de sodium : on envisage la réaction entre un volume Va= 20,0 mL d'une solution d'acide ascorbique HA de concentrationmolaire Ca= 1,00 10-2 mol/L et un volume Vb= 5,0 mL d'une solution aqueuse d'hydroxyde de sodium de concnetration molaire Cb= 2,00 10-2 mol/L. A 25° le pH de la solution vaut 4.
C. Titrage colorimétrique : on écrase un comprimé de "vitamine C 500" dans un mortier. On dissout la poudre dans un peu d'eau distillée et on introduit l'ensemble dans une fiole jaugée de 100,0 mL; on complète avec de l'eau distillée. On obtient la solution S1 de concentration en acide ascorbique C1. On prélève un volume V1= 20 mL de la solution S1 que l'on dose avec une solution d'hydroxyde de sodium de concentration molaire en soluté apporté C2 = 4,00 10-2 mol/L en présence d'un indicateur coloré convenablement choisi. L'équivalence est obtenue pour un volume de solution aqueuse d'hydroxyde de sodium VBE= 14,0 mL.
corrigé vitesse v= 1/V dx/dt avec V : volume de la solution (L) et x: avancement (mol) la vitesse est proportionnelle au coefficient directeur de la tangente à la courbe ci-dessus x= f(t). à t1 =50 min, la tangente est très inclinée sur l'horizontale ; à t2 =250 min, la tangente est peu inclinée sur l'horizontale : en conséquence v1>v2. Au cours du temps la concentration des réactifs diminue, donc la vitesse décroît. t½ : durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final.
HA+ HO- = A- + H2O [H3O+]= 10-pH = 10-4 mol/L ; [HO-]= 10-14 / 10-4 = 10-10 mol/L n(HO-) =[HO-] * volume du mélange (L) = 10-10* 0,025 =2,5 10-12 mol. à l'état initial, les quantités de matière valent : n(AH)= CaVa=20 10-3 * 10-2 = 2 10-4 mol ; n(HO-)= CbVb=5 10-3 * 2 10-2 = 10-4 mol.
à l'équivalence du dosage acide base , les quantités de matière des réactifs sont en proportions stoéchiomètriques C1V1= CbVBE soit C1 = CbVBE /V1=4 10-2*14/20 = 2,8 10-2 mol/L Qté de matière dacide ascorbique dans 100 mL : 2,8 10-3 mol masse d'acide ascorbique (g) = Qté de matière (mol) * masse molaire (g/mol) = 2,8 10-3*176,1 = 0,493 g. "vitamine C 500"
signifie : 500 mg de vitamine C dans le comprimé.
|
||||||||||||||||||||||||||||||||||
|
|