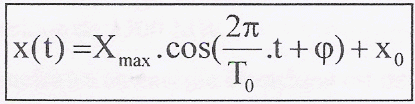Aurélie 04/05
QCM ;

association de résistors ; pendule élastique ; chimie ; acide base ; spectrophotométrie

physique : 1 h ; chimie : 30 min d'après concours kiné Berck 2005

Google

QCM ( 10 points)

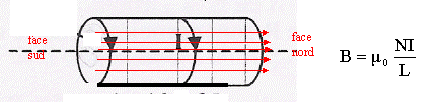
Un solénoïde de 500 spires, de longueur L= 60 cm est parcouru par un courant I= 5A.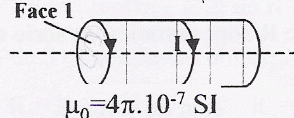

Parmi les affirmations suivantes, combien y-en-a-t-il d'exacte ?

  1. A l'extérieur du solénoïde le spectre magnétique est très semblable à celui d'un aimant droit.
  2. La face 1 du solénoïde est une face nord.
  3. A l'intérieur du solénoïde, les lignes de champ sont parallèles.
  4. A l'intérieur du solénoïde , la valeur du champ magnétique est inversement proportionnelle à la longueur L de la bobine.
  5. A l'intérieur du solénoïde, la valeur du champ magnétique est environ 5 mT.
corrigé
Le champ magnétique est pratiquement nul à l'extérieur du solénoïde : le spectre magnétique du solénoïde ne peut pas être semblable à celui d'un aimant droit.

La ressemblance est importante néanmoins, l'aimant droit ne possède que des plans de symétrie car c'est un parallélépipède rectangle tandis que le solénoïde possède un axe de révolution. Les lignes de champ résultante sont donc différentes en étant rigoureux.

Si l'aimantation de l'aimant est uniforme et que l'aimant est cylindrique, l'équivalence (à l'extérieur !) est rigoureusement exacte.

B= 4*3,14 10-7*500*5/0,6 = 5,2 10-3 T voisin 5 mT

3 affirmations exactes : 3, 4 et 5.

L'indice d'un verre, pour une radiation de longueur d'onde l se calcule par la formule de Cauchy : où A et B sont des constantes.

Pour la lumière rouge : l R= 775 nm ; indice nR= 1,617.

Pour la lumière violette : l V= 427 nm ; indice nR= 1,642.

Calculer l'indice du verre pour une radiation jaune l J= 579 nm.

corrigé
1,617 = A + B/(775 10-9)² =A + 1,665 1012 B.(1)

1,642 = A + B/(427 10-9)² =A + 5,485 1012 B.(2)

(2)-(1) donne : 0,025 = 3,82 1012 B ; B= 6,545 10-15 m-2.

d'où A = 1,606.

nJ= 1,606 + 6,545 10-15 / (579 10-9)²=1,626.

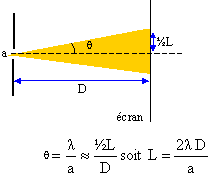
La lumière d'un laser est diffactée par une fente de largeur a. On observe la figure de fiffraction sur un écran à la distance D de la fente. La tache centrale a pour largeur L. La longueur d'onde du faisceau laser est l = 0,6328 mm. D= 2,5 m ; a= 0,2 mm.

Calculer la largeur L (cm) de la tache de diffraction.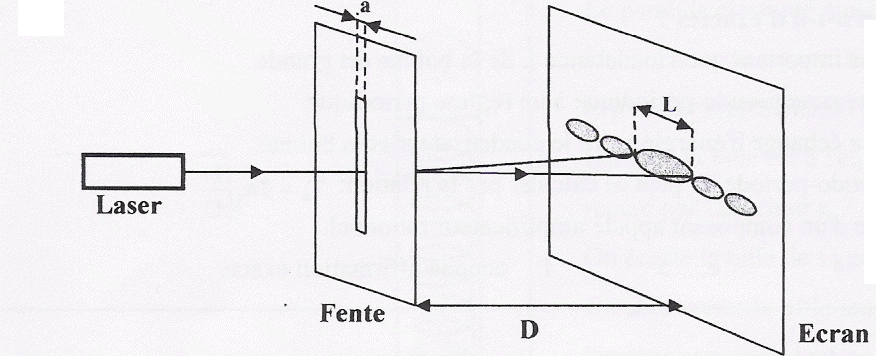

corrigé

L= 2*0,6328 10-6 * 2,5 / 2 10-4 = 1,58 10-2 m voisin 1,6 cm.

On considère un noyau de polonium 21084Po.

masse d'un neutron : mN= 1,0087 u ; masse du noyau de polonium : m= 210,0482 u ; masse proton mP= 1,0073 u ;

1u = 1,6604 10-27 kg ; 1 eV= 1,610-19 J ; c= 3 108 m/s.

Calculer l'énergie de liaison ( MeV/ nuclèons) par nucléons de ce noyau

corrigé

84 protons et 210-84 =126 neutrons

énergie de liaison : El = [84 mP+126mN-m]c²

84 mP+126mN-m=210,048284*1,0073+126*1,0084-210,0482 = 1,661 u

1,661 * 1,6604 10-27 = 2,76 10-27 kg

El = 2,76 10-27*(3 108 )²= 2,48 10-10 J

2,48 10-10 /1,6 10-19 = 1,55 109 eV = 1550 MeV

1550 / 210 = 7,4 MeV/nucléons.

La fission d'un noyau d'uranium 235 libère en moyenne une énergie de 200 MeV. Un réacteur nucléaire fournit une puissance de 1300 MW. Le rendement de la transformation d'énergie nucléaire en énergie thermique est de 30 %.

Masse d'un atome d'uranium 235 : =m= 235,0435 u.

Calculer la consommation annuelle d'uranium 235 (en tonne )du réacteur.

corrigé
200 106 eV soit 200 106*1,6 10-19 = 3,2 10-11 J.

Puissance thermique : 1300 106/0,3 = 4,3 109 W

énergie thermique produite en une année : 4,3 109*365*24*3600 = 1,37 1017 J.

nombre de fission en une année : 1,37 1017 / 3,2 10-11 = 4,27 1027 fissions.

soit 4,27 1027 atomes d'uranium 235 ayant été consommés.

masse d'un atome d'uranium 235 : 235,0438*1,66 10-27 = 3,9 10-25 kg.

perte de masse : 4,27 1027* 3,9 10-25 kg = 1,66 103 kg vosin 1,7 tonnes.

Un satellite décrit autour de la terre une orbite circulaire de rayon r avec une période T.

G = 6,67 10-11 SI ; rayon terrestre RT= 6380 km ; T= 1 h38 min ; masse de la terre MT= 5,98 1024 kg.

Calculer la vitesse (km/h) du satellite sur son orbite.

corrigé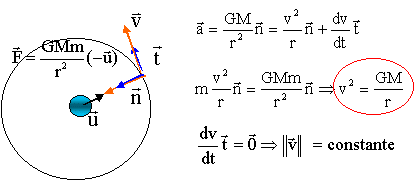

La période T est la durée pour pacourir une circonférence de rayon r à la vitesse v

2pr = vT

4p²r² = v²T² = GMT² / r

T² = r3 4p²/ (GM) d'où r3 = T² GM / (4p²).

T= 3600+38*60 = 5880 s

r3 = 5880²* 6,67 10-11 * 5,98 1024/(4*3,14²)= 3,5 1020.

r = racine cubique (3,5 1020) = 7,05 106 m

vitesse 2 = GM/r = 6,67 10-11*5,98 1024 / 7,05 106 = 5,65 107

prendre la racine carrée : 7,5 103 m/s = 7,5 km/s

7,5 * 3600 = 2,7 104 km/h.

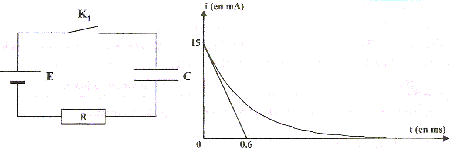Un condensateur initialement déchargé de capacité C et un conducteur ohmique R sont associés en série aux bornes d'un générateur idéale de tension de force électromotrice E= 9,0 V. A l'instant t=0, on ferme l'interrupteur K et on relève l'intensité du courant dans le circuit en fonction du temps t.

Déterminer les valeurs de la résistance R (kW) et de la capacité C (mF).

corrigé
à t= 0 le condensateur est déchargé ( la tension à ces bornes est nulle) et la tension aux bornes du résistor est E=9V, alors que l'intensité du courant vaut 0,015 A.

d'où R = E/I= 9 /0,015 = 600 W soit 0,6 kW.

La constante de temps du circuit vaut t= 0,6 ms ( mlecture graphe) soit RC= 6 10-4 s.

C= t / R = 6 10-4 / 600 = 10-6 F = 1 m F.

Un oscillateur électrique est constitué par l'association en série d'un condensateur de capacité C, d'une bobine d'inductance L et d'un conducteur ohmique de résistance R. Ce circuit est le siège d'oscillations électriques libres amorties.

Parmi les affirmations suivantes, combien y-en-a-t-il d'exactes ?

  1. L'amortissement des oscillations est d'autant plus grand que l'inductance de la bobine est grande.
  2. Quand la résistance R augmente, on passe d'un régime pseudo-périodique à un régime périodique.
  3. Dans un circuit oscillant faiblement amorti, il y a échange d'énergie entre le condensateur et la bobine.
  4. Pour des oscillations faiblement amorties, la pseudo-période T peut se calculer par la relation T= 2p(L/C)½.
  5. Il est possible d'entrtenir les oscillations à l'aide d'un composant appellé amplificateur opérationnel.
 

corrigé
L'amortissement des oscillations est d'autant plus grand que la résistance R est grande.

Quand la résistance R augmente, on passe d'un régime pseudo-périodique à un régime apériodique.

T= 2p(LC)½.

Il est possible d'entrtenir les oscillations à l'aide d'un montage simulant une résistance négative ( dans ce montage l'un des composants est un amplificateur opérationnel).

une seule affirmation juste : n°3.

Un condensateur de capacité C est initialement chargé sous une tension E. Il est ensuite associé à une bobine d'inductance L= 80 mH et de résistance négligeable. Le circuit ainsi constitué est le siège d'oscillations libres non amorties. La tension aux bornes du condensateur peut s'écrire : uC= 4,5 cos (5000 t) en unité SI.

Calculer la valeur maximale du courant I (mA) dans le circuit.

corrigé
Il y a échange d'énergie entre condensateur et bobine.

Lorsque la bobine stocke toute l'énergie du dipôle, l'intensité est maximale et E= ½LI²max.

Lorsque le condensateur stocke toute l'énergie, la tension uC est maxi male et E= ½Cu²Cmax.

conservation de l'énergie : ½LI²max.= ½Cu²Cmax.

I²max.=C/ L u²Cmax avec uCmax = 4,5 V

de plus 5000 rad/s = w0 = racine carrée (1/(LC))

soit 25 106 = 1/(0,08C) soit C= 5 10-7 F

I²max.=5 10-7 / 0,08 *4,5² = 1,26 10-4 A² soit Imax =1,12 10-2A voisin 11 mA.

Les niveaux d'énergie de l'atome d'hydrogène sont donnés par la relation : En = - 136 / n² avec En en eV et n supériuer ou égal à 1. h= 6,63 10-34 Js ; c = 3 108 m/s et 1 eV= 1,6 10-19 eV.

On considère l'ensemble des transitions des niveaux d'énergie caractérisés par n>2 au niveau d'énergie caractérisé par n=2. L'ensemble des radiations correspondantes forme la série de Balmer.

Calculer la plus grande longueur d'onde ( en nm) que peut avoir une radiation appartenant à cette série.

corrigé
E= hc/l soit l = hc/E

à la plus petite énergie correspond la plus grande longueur d'onde.

soit une transition du niveau 3 au niveau 2 : E= -13,6(1/9-1/4)= 1,889 eV

1,889*1,6 10-19 = 3,02 10-19 J

l = hc/E = 6,63 10-34 * 3 108 / 3,02 10-19 = 6,58 10-7 m soit 658 nm.
association de résistors : 5 points

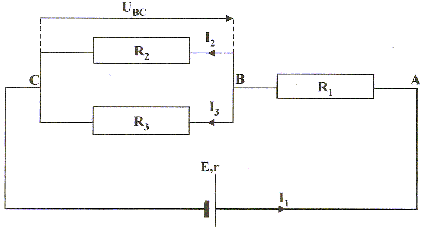
r= 8 W ; R1= 33 W ; R2 = 68 W ; R3 = 220 W ; uBC= 4,8 V

  1. Déterminer la résistance équivalente à R1, R2 et R3.
  2. Calculer la valeur de l'intensité I1 en mA.
  3. Déterminer la valeur de la force électromotrice E ( en V)
  4. Calculer la puissance électrique P ( en mW) fournie par le générateur au circuit.
  5. Déterminer la valeur de la puissance ( en mW) dissipée par effet joule entre B et C. 
corrigé
R2 et R3 en dérivation, alors leurs conductances s'ajoutent :

G3 = 1/R3 = 1/220 = 4,55 10-3 S ; G2 = 1/R2 = 1/68 = 1,47 10-2S

G = G3 + G2 = 1,93 10-2 S

R4 résistance équivalente à R3 et R2 : R4 = 1/G= 1/1,93 10-2 = 51,9 W.

uBC= R4 I1 soit I1 = uBC/ R4 =4,8 / 51,9 = 9,25 10-2 A = 92,5 mA.

R4, R1 et r en série équivalents à : Réqui = R4+ R1 + r = 51,9 + 33+8=92,9 W.

E= Réqui I1 = 92,9*9,25 10-2 = 8,6 V.

Puissance fournie au circuit : P= uAC I1 avec uAC= E-rI1 = 8,6-8*9,25 10-2 =7,86 V

P= 7,86*9,25 10-2 = 0,73 W = 730 mW.

Puissance joule dissipée entre B et C : PJ = R4 I²1 = uBC I1= 4,8*9,25 10-2 =0,440 W = 444 mW.
pendule élastique : 5 points

Une bille de masse m est reliée à l'extrémité d'un ressort à spires non jointives de constante de raideur k, de masse négligeable et de longueur à vide l0.

Le pendule élastique ainsi constitué peut osciller verticalement sans frottement.

L'abscisse x du centre d'inertie de la bille est repéré par l'axe Ox. Le point O représente l'origine de l'axe des abscisses.

Lorsque la bille est à l'équilibre, la position du centre d'inertie G est repérée par l'abscisse x0.

On écarte la bille de sa position d'équilibre de 2 cm vers le bas.

On abandonne la bille sans vitesse et on choisit comme origine des temps, l'instant correspondant au premier passage du point G par la position d'équilibre.

masse du mobile m = 120 g

k= 42 N/m

l0 = 20 cm.

  1. Calculer x0 ( en cm), abscisse de la position d'équilibre.
  2. Calculer l'énergie mécanique Em ( en mJ) de la bille lors des oscillations. On choisit comme origine de l'énergie potentielle de pesanteur le plan horizontal contenant le point O.
  3. Déterminer la vitesse maximale ( en m/s) du centre d'inertie G.
    L'équation horaire du mouvement peut s'écrire :
  4. Donner l'équation horaire du mouvement de G en unité SI.
  5. Calculer l'énergie cinétique Ec( en mJ) du système à l'instant t = 0,27 s.
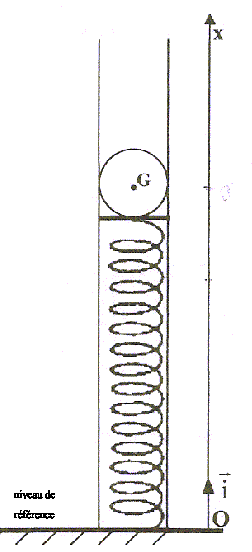
corrigé
x0 ( en cm), abscisse de la position d'équilibre :

La bille, posée sur le ressort est soumise à deux forces opposées : son poids et à la tension du ressort comprimé.

mg = k((l0-l) ; l0-l = mg/k ; l = l0 - mg/k = 0,2 - 0,12*9,8/42 = 0,172 m = 17,2 cm ; x0 = 17,2 cm.

L'énergie mécanique est la somme des énergies potentielles élastique et de pesanteur, et de l'énergie cinétique : on choisit comme référence de l'énergie potentielle élastique x = l0 ( ressort non déformé) et comme référence de l'énergie potentielle de pesanteur le point O.

Em = ½mv² + ½k(x-l0)² + mgx

en absence de frottement l'énergie mécanique se conserve.

Energie mécanique à la position la plus basse, dans laquelle la vitesse est nulle : (l0 -x = 0,048 m ; h = 0,152 m )

Em = ½k(l0 -x)² + mg h = 0,5 *42*0,048² + 0,12*9,8*0,152 =0,227 J = 227 mJ.

 Lors du passage à la position x = x0, l'énergie potentielle élastique vaut ½k(x0-l0)² l'énergie cinétique est maximale, l'énergie potentielle de pesanteur vaut mgx0 :

Em = ½mv²max + mgx0 +½k(x0-l0)²= 0,227 J

v²max = 2*0,227/m-2gx0-k/m(x0-l0)²=0,454/0,12 -2* 9,8*0,172-42/0,12*0,028²]= 0,137 soit vmax = 0,37 m/s.

Xmax = 0,02 m ; w0= (k/m)½ = (42/0,12)½ = 18,71 rad/s

à t= 0 , x = x0 = 0,172 m : 0,172 = 0,02 cos j0+0,172 donne cos j0=0 soit j0=+½p ou j0=-½p

v(t) = dx(t) / dt= -0,02*18,71 sin (18,71 t+j0) = -0,374sin (18,71 t+j0)

Or à t=0 la vitesse a le sens de l'axe et vaut 0,37 m/s d'où j0=-½p

x(t) = 0,02 cos (18,71 t-½p) + 0,172.

v(t) = dx(t) / dt= -0,02*18,71 sin (18,71 t-½p) avec Vmax = 0,374 m/s.

v(t) = 0,374 sin (18,71 t+½p)

énergie cinétique à t = 0,27 s :

v = +0,374 sin (18,71*0,27+ 1,57)= 0,332 m/s

Ec = 0,5 mv² = 0,5*0,12*0,332²= 6,6 10-3 J voisin 6,6 mJ.
QCM chimie ( 5 points)

H : 1 ; C : 12 ; O : 16 ; S : 32 ; Na : 23 g/mol

Une bouteille métallique de 100 L contient initialement du dioxygène à la température de 23 °C et à la pression de 120 bars. Après utilisation, le dioxygène se trouve à la pression de 40 bars et à la température de 15°C. On admet que O2 suit la loi des gaz parfaits. R= 8,31 SI ; 1 bar = 105 Pa.

  1. Calculer la masse ( en kg) de dioxygène utilisé.
corrigé
Qté de matière initiale dioxygène : n0 = P0V/(RT0) avec V= 0,1 m3 ; P0 = 1,2 107 Pa et T0 = 273+23 = 296 K

n0 = 1,2 107*0,1 / (8,31*296)=4,88 102 mol

Qté de matière finale dioxygène : nf = PfV/(RTf) avec V= 0,1 m3 ; Pf = 4 106 Pa et Tf = 273+15 = 288 K

nf = 4 106*0,1 / (8,31*288)=1,67 102 mol

n0 -nf =321 mol

masse (g) = Qté de matière (mol) * masse molaire (g/mol) = 321*32 = 1,03 104 g = 10,3 kg.

On mesure à 25 °c la conductance d'une solution aqueuse de nitrate d'argent à l'aide d'un générateur de tension sinusoïdale, de deux électrodes, d'un voltmètre et d'un ampèremètre. La distance entre les deux électrodes est L= 5,0 mm et la surface de chaque électrode est S= 1,2 cm².

Le voltmètre indique une tension efficace Ueff = 4,21 V et l'ampèremètre une intensité efficace ieff = 8,54 mA.

l(Ag+)= 6,19 mS m² mol-1 ; l(NO3-)= 7,14 mS m² mol-1 ;

  1. Déterminer la concentration en mmol/L de la solution de nitrate d'argent.
corrigé
conductance de la portion de solution comprise entre les plaques : G = Ieff / U eff = 8,54 / 4,21 = 2 mS

constante de cellule : k = L/S = 5 10-3 / 1,2 10-4 = 41,7 m-1

conductivité s =kG= 41,7*2 = 83,4 mS m-1.

s =lAg+[Ag+] +lNO3-[NO3-]=(lAg++lNO3-) c avec c=[NO3-]=[Ag+] mol m-3.

c =s /(lAg++lNO3-) = 83,4 / (6,19 + 7,14)= 6,25 mol m-3 voisin 6,3 mmol/L.

On réalise la déshydratation d'un volume de 15 L de butan-2-ol. On obtient une masse de 6,6 kg de but-2-ène. Densité de l'alcool d= 0,81.

  1. Calculer le rendement de cette transformation.
corrigé
alcool : C4H10O : Malcool = 4*12+10+16=74 g/mol ; alcène C4H8 : Malcène = 56 g/mol

masse d'alcool : 15+0,81 =12,15 kg = 1,21 104 g.

Qté de matière alcool (mol) = masse (g) / masse molaire butan-2-ol) (g/mol) =1,21 104 /74 =164,2 mol

C4H10O --> C4H8 + H2O

On obtient 164,2 mol de but-2-ène

soit une masse m =164,2*56 =9,2 kg

rendement : 6,6/9,2*100 = 72%.

Les ions thiosulfate S2O32- réagissent avec le diiode I2 en solution pour donner des ions iodure I- et des ions tétrathionate S4O62-. On verse 15 mL de solution de diiode de concentration C= 6 10-3 mol/L dans une solution contenant des ions thiosulfate.

  1. Déterminer la quantité maximale ( en micromole) d'ions thiosulfate pouvant réagir avec le diiode.
corrigé
2S2O32- + I2 = 2 I- + S4O62-.

à l'équivalence : n thiosulfate = 2nI2 =2*15 10-3*6 10-3 = 180 10-6 mol = 180 mmol.

On verse une solution acidifiée de permanganate de potassium dans un tube à essai contenant de l'éthanol. La transformation chimique ayant liau a pour équation :

2 MnO4- + 5 CH3-CH2OH + 6H+ --> 5 CH3-CHO + 2Mn2+ + 8H2O

Parmi les affirmations suivantes, combien y-en-a-t-il d'exactes ?

  1. L'éthanol joue le rôle de réducteur. exact
  2. Les ions permanganate libèrent 5 électrons exact MnO4- + 8H+ + 5e-= Mn2+ + 4H2O.
  3. Il s'agit d'une réaction de réduction ménagée d'un alcool faux, oxydation ménagée d'un alcool.
  4. Le produit formé est une cétone faux, un alcool primaire conduit d'abord à un aldehyde.
  5. Un test à la DNPH en fin de réaction donne une couleur jaune, caractéristique du groupe carbonyle.exact
3 affirmations exactes.
acide base( 5 points)

On utilise pour diminuer le pH de l'eau d'une piscine, une poudre contenant de l'hydrogénosulfate de sodium NaHSO4. On introduit dans un bécher 0,80 g de cette poudre et on ajoute un volume de 10 mL de soude de concentration CB= 2,00 mol/L. La transformation chimique ayant lieu a pour équation : HO- + HSO4- = SO42- + H2O.

On introduit la soude en excès par rapport aux ions hydrogènosulfate. On dose alors l'excès de soude par une solution d'acide chlorhydrique de concentration CA= 2,00 mol/L. Il faut verser VAE= 6,9 mL d'acide pour onbtenir l'équivalence acido-basique.

couple (HSO4-/SO42-) Ka1 = 1,25 10-2 ; produit ionique de l'eau Ke = 10-14.

  1. Calculer la constante K associée à l'équation de la transformation
  2. Déterminer la quantité nHO- ( en mmol) d'ion HO- ayant réagi avec la poudre.
  3. Déterminer le pourcentage massique P d'hydrogénosulfate de sodium dans la poudre.
corrigé
HO- + HSO4- = SO42- + H2O : K= [SO42-]/([HSO4-][HO-])

K= [SO42-][H3O+]/([HSO4-][HO-][H3O+]) = Ka1 / Ke = 1,25 10-2/10-14 = 1,25 1012.

quantité de matière ( en mmol) d'ion HO- ayant réagi avec l'acide : CA VAE = 2*6,9 =13,8 mmol

quantité de matière initiale ( en mmol) d'ion HO- : 2*10 = 20 mmol

quantité nHO- ( en mmol) d'ion HO- ayant réagi avec la poudre : 20-13,8 = 6,2 mmol.

d'où la Qté de matière d'hydrogénosulfate contenu dans la poudre : 6,2 mmol.

masse molaire NaHSO4 : 23+1+32+4*16 = 120g/mol

masse hydrogénosulfate de sodium : 120*6,2 10-3 = 0,744 g

pourcentage massique P = 0,744/0,8*100 = 93 %.
spectrophotométrie ( 5 points)

On se propose de déterminer la concentration d'une solution de permanganate de potassium par spectrophotométrie. On dispose d'une solution S0 de permanganate de potassium de concentration connue C0 = 10-3 mol/L. On prépare 5 solutions étalons à partir de la solution précédente en suivant le processus suivant :

On prélève V0 mL de S0 que l'on verse dans une fiole jaugée de 50 mL et on complète avec de l'eau distillée jusqu'au trait de jauge.
solution
S1
S2
S3
S4
S5
volume V0 (mL)
5
10
15
20
25
On dispose ainsi d'une échelle de teintes qui permet de déterminer approximativement la concentration C de la solution S par comparaison. La solution S est trop concentrée et on la dilue 100 fois ; on obtient la solution S'.

La teinte de la solution S' est comprise entre les teintes des solutions S2 et S4.

A l'aide d'un spectrophotomètre, on mesure l'absorbance des 5 solutions de l'échelle de teintes et de la solution diluée S'. L'absorbance est mesurée pour une longueur d'onde l= 530 nm qui correspond au maximum d'absorption de la solution de permanganate. L'épaisseur de la cuve est L= 1 cm.
solution
S1
S2
S3
S4
S5
S'
absorbance A
0,23
0,46
0,69
0,92
1,15
0,57

  1. Donner un encadrement ( en mol/L) de la valeur de la concentration de la solution S.
  2. Calculer la valeur du coefficient d'extinction molaire e ( en L mol-1 cm-1)
  3. En déduire la valeur de la concentration C de la solution S ( en mol/L).
corrigé
solution
S1
S2
S3
S4
S5
volume V0 (mL)
5
10
15
20
25
facteur de dilution F
50/5= 10
50/10 = 5
50/15= 3,33
50/20=2,5
50/25 = 2
concentration (mol/L) : C0/F
10-3 / 10 = 10-4
2 10-4
3 10-4
4 10-4
5 10-4
2 10-4<concentration de la solution S'<4 10-4 mol/L

en tenant compte de la dilution : 2 10-2<concentration de la solution S<4 10-2 mol/L

A= e CL loi de Beer Lambert

pour la solution S1 par exemple : C= 10-4 mol/L ; L= 1 cm et A = 0,23

e = A/(CL)= 0,23 / 10-4 = 2300 L mol-1 cm-1

pour la solution S' : C= A / (eL) = 0,57 / (2300*1)= 2,48 10-4 mol/L

soit pour la solution S : 2,48 10-2 mol/L
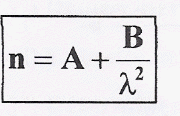retour -menu