Aurélie dec 04
statique et dynamique des fluides ;

chauffage de l'eau d'une piscine ; acoustique

d'après bts enveloppe du bâtiment 2004

Google

statique et dynamique des fluides ( 7 points)

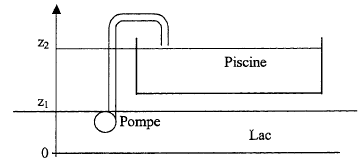
Dans un club de vacances, on construit une piscine à proximité d'une retenue d'eau. La piscine a les dimensions suivantes : longueur a = 25 m ; largeur b = 15 m ; profondeur utile ( hauteur d'eau) h= 2 m

Données : pression atmosphérique P= 105 Pa. ; masse volumique de l'eau r = 1000 kg m-3 ; g = 9,8 m/s²

équation Bernoulli généralisée : m( P2-P1) / r + ½ m(v2²-v1²) + mg(z2-z1)=W12.

I.

  1. Donner l'expression littérale de la force pressante due à l'eau, notée Fp, s'exerçant sur l'une des deux plus grandes parois verticales de la piscine remplie d'eau.
  2. Donner l'expression littérale de la force pressante due à l'eau, notée Fb, s'exerçant sur l'une des deux plus petites parois verticales de la piscine remplie d'eau, ainsi que la force pressante Ff s'exerçant sur le fond de la piscine remplie d'eau.
  3. Faire les applications numériques.
  4. L'eau est puisée par 4 pompes dans le lac de retenue. La côte de niveau de ce dernier est z1 = 825 m. La surface libre de l'eau dans la piscine est à la côte z2 = 850 m

    - La canalisation de sortie de chacune des pompes a un diamètre d = 50 mm. La vitesse du fluide dans cette canalisation est v= 3 m/s. calculer le débit volumique Qv de la pompe.
    - Calculer le volume d'eau contenu dans la piscine. En déduire la durée du remplissage de la piscine, les 4 pompes étant en service.
    - En utilisant l'équation de Bernoulli généralisée, calculer l'énergie dépensée par une pompe pour remplir la piscine. En déduire la puissance théorique Pth d'une pompe.
    - Les pompes ont un rendement de 80 %, calculer la puissance électrique Pé consommée par une pompe pour remplir la piscine.

 

corrigé
On considère une surface de longueur a et de hauteur très petite notée dz, située à l'altitude z par rapport au fond de la piscine.

pression exercée par une hauteur d'eau ( h-z) à l'altitude z : p= rg(h-z)

surface élémentaire notée dS= a dz

force pressante élémentaire notée dF exercée sur cette surface : dF= p dS = rg(h-z) a dz= rgahdz - rgazdz

intégrer entre z= 0 et z=h : Fp= [rgahz]0h - [½rgaz2]0h =rgah2- ½rgah2= ½rgah2.

Fp= 0,5 103 *9,8*25*2² = 4,9 105 N.

même résultat sur la petite surface en remplaçant a par b : Fa=½rgbh2.

Fp= 0,5 103 *9,8*15*2² = 2,94 105N.

sur le fond : surface S= ab ; pression exercée par une hauteur h d'eau = rgh ;

pression due à l'air : 105 Pa ; pression totale : rgh + 105 ; Ff= ab (rgh + 105).

Ff= 25*15(103*9,8*2+105)=4,48 107 N.

débit volumique Qv (m3/s) = vitesse (m/s) * section (m²)

section : 3,14 * (25 10-3)² =1,96 10-3 m² ; Qv= 3 * 1,96 10-3 =5,89 10-3 m3/s.

volume d'eau de la piscine : V = abh = 25*15*2 = 750 m3.

débit des quatre pompes : 2,36 10-2 m3/s ;

durée (s) de remplissage = volume (m3) / débit ( m3/s) = 750 / 2,36 10-2 = 3,18 104 s = 8,84 h.

m( P2-P1) / r + ½ m(v2²-v1²) +m g(z2-z1)=W12.

( P2-P1) = 0 ; les surfaces libres de l'eau sont à la même pression atmosphérique

La surface du lac est très grande par rapport à la surface de la piscine donc (v2²-v1²) = v2²

(z2-z1) = 25 m ; m = masse d'eau contenue dans la piscine = 7,5 105 kg.

W12 = ½m v2² + mg(z2-z1)=(0,5 * 3² + 9,8*25 ) 7,5 105 = 1,87 108 J.

soit pour une pompe : 4,68 107 J.

puissance théorique ( W) = énergie (J) / durée (s) = 4,68 107 / 3,18 104 = 1,47 kW.

puissance électrique = Pth / rendement = 1,47 / 0,8 = 1,84 kW.

chauffage de l'eau d'une piscine (6 points)

La température de l'eau puisée dans le lac est q1 = 15°C. On veut une température égale à q 2 = 25 °C dans la piscine.

capacité thermique de l'eau c= 4,185 kJ kg-1 K-1 ; pouvoir calorifique du méthane CH4 : Q0 = 890 kJ/mol ; volume molaire 25 L/mol ; température ambiante de l'air q = 25 °C ; H: 1 ; C : 12 ; O : 16 g/mol

Le chauffage est assuré par une chaudière à gaz, ici du méthane.

  1. Calculer la quantité de chaleur Q nécessaire pour chauffer l'eau de la piscine.
  2. Calculer la quantité de matière n (mol) de méthane pour amener l'eau de la piscine à 25 °C.
  3. En réalité le rendement du système de chauffage est 0,7. Calculer la masse réelle de méthane consommée.
    - Calculer le volume de méthane utilisé.
    - Ecrire l'équation chimique de la réaction du méthane avec l'oxygène, en supposant la combustion complète.
    - Calculer le volume d'oxygène réellement consommé.
    - En déduire le volume d'air utilisé sachant que l'air contient 20% en volume de dioxygène.
corrigé
Q= mc D q avec m = 7,5 105 kg et D q = 10 °C

Q= 7,5 105*4,185 *10 = 3,14 107 kJ.

quantité de matière n (mol) de méthane = Q / pouvoir calorifique méthane = 3,14 107 / 890 = 3,53 104 mol.

en tenant compte du rendement, la quantité de matière réelle de méthane est : 3,53 104 / 0,7 = 5 104 mol

masse molaire méthane : 12 + 4 = 16 g/ mol

masse réelle (g) = quantité de matière (mol) * masse molaire (g/mol)

m = 5 104 *16 = 8,06 105 g = 8,06 102 kg.

volume de gaz (L) = quantité de matière (mol) * volume molaire ( L/mol) = 5 104 *25 = 1,25 106 L = 1250 m3.

CH4 +2 O2 = CO2 + 2H2O

d'après les coefficients de l'équation, à une mole de méthane correspond 2 moles de dioxygène

Qté de matière dioxygène = 2 * 5 104 = 105 mol O2.

volume dioxygène : 25 * 105 L = 2,5 103 m3.

volume d'air : 5* 2,5 103 = 1,25 104 m3.
acoutique (7 points)

On se propose de réaliser l'analyse acoustique d'un local séparé de l'extérieur par une paroi. L'étude consiste à déterminer l'isolement acoustique de cette paroi.

Une source sonore (pompes) est placé à l'extérieur du local ; elle émet un niveau sonore d'émission Le dont l'analyse par bande d'octave, est donné ci-dessous. Un sonomètre placé à l'extérieur du local permet de relever le niveau sonore de réception Lr.
fréquence médiane de la bande d'octave (Hz)
125
250
500
1000
2000
4000
niveau sonore d'émission Le ( dB)
79,3
77
79
77,8
74,1
71,9
niveau sonore de réception Lr ( dB)
48,8
46,1
44,8
46,2
42,8
38,5

  1. Etude de l'isolement brut de la paroi :
    - Déterminer les intensité sonores d'émission notées I125 et I1000 correspondant aux fréquences 125 et 1000 Hz. I0 = 10-12 W/m2.
    - Calculer le niveau sonore global d'émission Leg correspondant à l'ensemble des fréquences.
    - Calculer le même niveau sonore global de réception Lrg.
    - En déduire l'isolement brut Db de la paroi.
  2. Influence d'une porte : On suppose que la paroi précédente comporte une porte ; entre le bas de la porte et le plancher se trouve 1 cm de "vide". Les nouvelles caractéristiques de la paroi sont les suivantes :

    Mur : facteur de transmission tm= 10-3. hm = 2,5 m ; lm= 5 m
    Porte : facteur de transmission     tp= 10-2. hp = 2 m ; lp= 1 m
    Interstice sous la porte : indice d'isolement acoustique Rv =0. hv = 1 cm ; lv= 1 m
    Formulaire : R= 10 log 1/    t ; t i = St iSi/SSi ( i représente chaque élément de la paroi)
    Db = R +10 log (A/S) ; A représente l'aire d'absorption équivalente du local A = 25,5 m² , S représente la surface de la paroi extérieure.
    - Calculer la surface de la porte ainsi que la surface de la partie "vide" sous la porte.
    - Montrer que le facteur de transmission     t v de la partie "vide " est égal à 1.
    - Calculer le facteur de transmission moyen de la paroi et en déduire l'affaiblissement R de cette paroi.
    - Déterminer l'isolement brut D'b de la paroi comportant la porte.
    - Comparer au résultat ci-dessus et conclure.

corrigé
L= 10 log (I/I0) s'écrit : L/10 = log (I/I0) puis 10L/10 = I/I0 ; I= I0 10L/10 = 10-12 10L/10

bandes d'octaves en Hz
125
250
500
1000
2000
4000
niveau d'intensité L (dB)
79,3
77
79
77,8
74,1
71,9
intensité sonore Wm-2
10-12 107,93

= 10-4,07

=8,51 10-5
10-12 107,7

= 10-4,3

= 5 10-5
10-12 107,9

= 10-4,1

=7,94 10-5
10-12 107,78

=10-4,22

=610-5
10-12 107,41

= 10-4,59

=2,57 10-5
10-12 107,19

= 10-4,81

=1,55 10-5
Les intensité sonores s'ajoutent : Itotal = 8,51 10-5 + 5 10-5+7,94 10-5+610-5+2,57 10-5 +1,55 10-5=3,16 10-4 W/m²

Leg= 10 log (3,16 10-4 / 10-12) = 85 dB.

bandes d'octaves en Hz
125
250
500
1000
2000
4000
niveau d'intensité L (dB)
48,8
46,1
44,8
46,2
42,8
38,5
intensité sonore Wm-2
10-12 104,88

= 10-7,12

=7,58 10-8
10-12 104,61

= 10-7,39

= 4,07 10-8
10-12 104,48

= 10-7,52

=3,02 10-8
10-12 104,62

=10-7,38

=4,1710-8
10-12 104,28

= 10-7,72

=1,9 10-8
10-12 103,85

= 10-8,15

=7,08 10-9
Les intensité sonores s'ajoutent : Itotal = 7,58 10-8 + 4,07 10-8+3,02 10-8+4,1710-8+1,910-8 +7,08 10-9=2,14 10-7 W/m²

Lrg= 10 log (2,14 10-7 / 10-12) = 53,3 dB.

l'isolement brut entre ces deux parois est R =85-53,3 = 31,7 dB.

l'indice d'affaiblissement global de la paroi:

Db = R +10 log (A/S)= 31,7 + 10 log (25,5 / 7,5) = 37 dB.

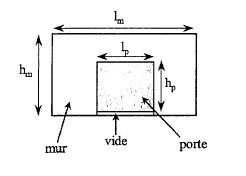
Surface de la porte : 2 m² ; surface de la partie "vide" sous la porte : 0,01 m² ;

indice d'isolement acoustique Rv = 10 log 1/t v = 0 soit log 1/t v 0 et t v = 1.

facteur de transmission global tg de la paroi composée t g= St iSi / S Si.

S Si = surface totale = 2,5*5 = 12,5 m² ; surface mur = 12,5-2-0,01 = 10,49 m²

t g= (10-2 *2 + 10-3 *10,49 + 1*0,01)/ 12,5 = 3,24 10-3.

indice d'affaiblissement global Rg = 10 log (1/tg ) = 10 log (1/3,24 10-3) = 24,9 dB.

isolement brut D'b de la paroi comportant la porte :

D'b = Rg +10 log (A/S)= 24,9 + 10 log (25,5 / 12,5) = 28 dB.

Cette valeur est inférieure de 8 dB par rapport au mur sans porte : la présence d'une porte atténue moins le bruit extérieur.
retour -menu