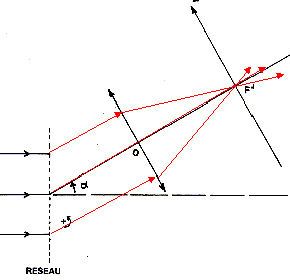
.Un spectrophotomètre est constitué:

o d'une partie optique: source, monochromateur à réseau, cuve à échantillon

o d'une partie électronique: photodiode, chaîne de traitement du signal et affichage de l'absorbance.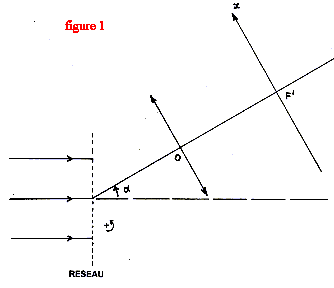

Etude de la partie optique:

Le réseau représenté figure 1 comporte n = 1000 traits par millimètre.

Une lentille de distance focale f = 20 cm est placée derrière le réseau, son axe principal faisant un angle a de 30° avec la normale au réseau. On place en F' une fente centrée sur cet axe dans le plan focal image.

1. On note i l'angle d'incidence sur le réseau, i' l'angle d'émergence. Les angles sont orientés de la normale au réseau vers le rayon ; le sens positif est le sens trigonométrique. Etablir, schéma à l'appui, la relation du réseau liant i, i', l'ordre de diffraction k, n et l la longueur d'onde de la lumière utilisée : sin i'- sin i = knl
2. Le réseau est éclairé sous incidence normale (i = 0) et, pour toute cette question, on utilise le spectre d'ordre k = 1.
   -Pour quelle longueur d'onde l₀ obtient-on une image au foyer principal F' de la lentille ?
   - Compléter le schéma de la figure 1 en traçant la marche des trois rayons lumineux de longueur d'onde l₀ depuis la sortie du réseau jusqu'au plan focal image de la lentille.
   - On donne l'expression de la dispersion angulaire di'/dl autour de l₀ : di'/dl =n/ cosa . Faire l'application numérique.
   - Pour une longueur d'onde l, voisine de l₀ (l < l₀ ), on obtient une image en un point d'abscisse x (x petit devant f) dans le plan focal de la lentille. Compléter le schéma 1 en faisant figurer les trois rayons de longueur d'onde l. Montrer que : x = f.n.(l - l₀ )/ cosa
   - En fait, l'ensemble des rayons dont la longueur d'onde est comprise entre l₀ - D l/2 à l₀ + D l/2 passe par la fente F' de largeur 2x. Calculer la bande passante D l du monochromateur ainsi obtenu pour x = 1 mm.

---

corrigé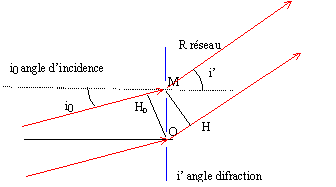

---

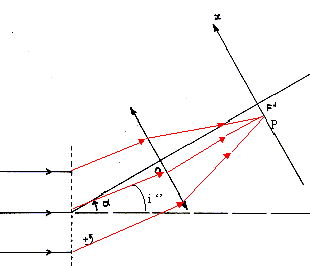
Les rayons incidents sont parallèles ansi que les rayons réfractés..

La différence de chemin optique entre le rayon passant par le point O et celui passant par le point homologue M vaut ( l'indice de l'air vaut 1) : OM = a

OH-MH₀ = a sin i'- a sin i₀ = a( sini'-sin i₀) avec a = 1/n ; n pas du réseau en nombre de traits / m.

Le interférences sont constructives entre les ondes diffractées si la différence de marche est un multiple de la longueur d'onde l.

1/n ( sini'-sin i₀) = kl avec k entier positif, nul ou négatif

sin i'-sin i₀ = kl n.

---

sin i₀ = 0 et k=1 ; sin i' = l n.

un rayon incident parallèle à l'axe optique principal de la lentille émerge en passant par le foyer principal image F' :

donc i' = a = 30 ° ; l₀= sin a / n= 0,5 10^-6 = 5 10^-7 m = 500 nm.

Lorsque deux ondes planes, de longueurs d'ondes voisine l et l +dl, tombent sur un réseau en faisant le même angle d'incidence i₀, l'écart di entre les angles que font les ondes diffractées, s'obtient en différentiant l'équation :

sin i'-sin i₀ = kl n ; cos i' di'= kn dl. ; di'/ dl = kn /cos i'.

pour k=1 la dispersion angulaire vaut : n/ cos a = 10⁶ /cos30=1,15 10^-6.

l <l₀ ; sin i'' = nl ; sin a = nl₀ ; donc i'' <a.

tan(a-i") = x/ f voisin de (a-i") radian ; x = f (a-i") = f di'

or di' = n dl /cos a pour k= 1

x= f n dl /cos a = f n (l₀-l) /cos a

x = f.n.(l - l₀ )/ cosa donne D l = (l - l₀ ) = x cosa / (fn)

D l = 10^-3*cos 30 / ( 0,2*10⁶) = 4,3 10^-9 m = 4,3 nm.

---

---

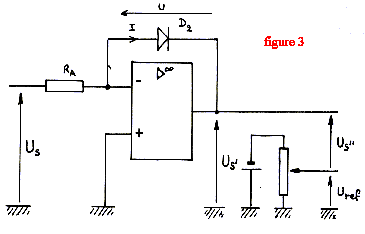
Les amplificateurs opérationnels (AOP) sont considérés comme parfaits : courants d'entrée : i⁺ = i^- = 0 et tension différentielle d'entrée : e = 0

Le faisceau de lumière monochromatique issu de la cuve du spectrophotomètre contenant la substance absorbante est reçu par une photodiode dont le courant inverse IA est proportionnel à la puissance énergétique P (ou flux énergétique) reçue : I_A = K. P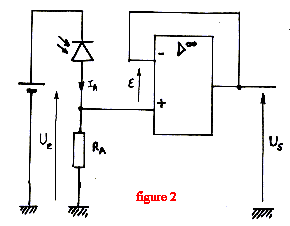

On réalise le montage schématisé figure 2

1. Exprimer la tension U_e aux bornes de la résistance R_A, puis la tension U_s à la sortie du premier amplificateur opérationnel, en fonction de P.
2. On complète le montage de la figure 2 en ajoutant celui de la figure 3. La tension U_s est envoyée à l'entrée d'un deuxième amplificateur opérationnel dont la tension de sortie est U_s'. La diode à jonction D₂ placée en dérivation entre l'entrée inverseuse et la sortie de cet amplificateur opérationnel a une caractéristique I = f(U) dont l'équation peut se mettre sous la forme I = I₀ exp( kU). Etablir la relation : U_s' = - k" ln(K . P/ I₀)
3. On mesure la tension U_s" = U_s' - U_ref. La substance de référence étant placée dans la cuve, on règle U_ref grâce au potentiomètre R de façon à obtenir U_s" = 0. (la puissance énergétique reçue par le capteur est alors P = P₀) On place l'échantillon étudié dans la cuve, on lit une tension U_s" non nulle, la puissance reçue par le capteur est alors P.
   - Exprimer la tension U_ref lorsque le réglage du zéro est effectué, en fonction de P₀.
   - Exprimer U_s " lorsque l'échantillon est dans la cuve en fonction de P et P₀.
   - Montrer que U_s" est proportionnelle à l'absorbance A de la solution.
   On rappelle que Lnx == 2,3 logx
   - Calculer A lorsque k = 12,9 mV^-1 et U_s"= 0, 170 mV.

Le principe d'un réfrigérateur à compression peut être ramené au schéma de la figure 4.

Le système fonctionne selon un cycle réversible et le fluide utilisé est l'ammoniac.

Le cycle est schématisé dans le diagramme entropique de la figure 5, où est représentée en pointillés la courbe de saturation (l'entropie S en abscisse, la température absolue T en ordonnée).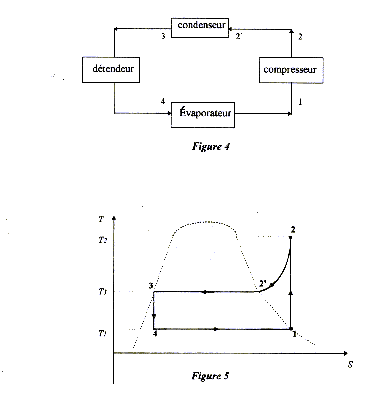

1. Le fluide sort de l'évaporateur dans l'état 1 (température T₁= 263 K, pression P_l = 2,9.10⁵ Pa) sous forme de vapeur saturante. Il passe alors dans le compresseur où il subit une compression adiabatique réversible. Il sort du compresseur (à l'état de vapeur sèche) dans l'état 2 (température T₂ et pression P₂ = 10,2. 10⁵ Pa). En assimilant l'ammoniac gazeux à un gaz parfait, calculer la température T₂ en fin de compression.
2. De 2 en 2', l'ammoniac se refroidit de manière isobare, de la température T₂ à la température T₃ = 298 K. Calculer la quantité de chaleur Q₂ échangée par 1 kg de fluide avec le milieu extérieur au cours de ce refroidissement. Commenter son signe.
3. L'ammoniac est dans l'état 2' sous forme de vapeur saturante. Il pénètre alors dans le condenseur où il se liquéfie à la pression P₃ = P₂ et à la température T₃. A la sortie du condenseur en 3, le fluide est à l'état de liquide de saturation. Calculer la quantité de chaleur Q₃ échangée par 1 kg de fluide avec le milieu extérieur au niveau du condenseur. Commenter son signe.
4. Le liquide pénètre alors dans le détendeur. De 3 à 4, il subit une détente adiabatique et réversible, au cours de laquelle une partie du liquide se vaporise. Ainsi, à son entrée en 4 dans l'évaporateur, la masse d'ammoniac sous forme vapeur est égale à 15 % de la masse totale d'ammoniac (liquide + vapeur). La vaporisation du liquide restant va se terminer dans l'évaporateur à la pression P₁ et à la température T₁. Calculer la masse de liquide qui va se vaporiser, dans l'évaporateur pour 1 kg de fluide.
   -Calculer la quantité de chaleur Q, échangée par 1 kg de fluide avec le milieu extérieur au niveau de l'évaporateur. Commenter son signe.
5. Calculer la quantité de chaleur totale échangée par 1 kg de fluide avec le milieu extérieur au cours du cycle.
6. Déduire du premier principe le travail W échangé par 1 kg de fluide avec le milieu extérieur au cours du cycle. Commenter son signe.
7. Calculer l'efficacité de la machine frigorifique e = Q₁/ W. Où doit-on placer le compartiment à refroidir et pourquoi ?

Données :

Capacité thermique massique moyenne de l'ammoniac gazeux, à pression constante, entre les températures T₂ et T₃ :
Cp = 2,12 kJ.K^-1.kg^-1

g = 1,30 (rapport des capacités thermiques massiques du gaz à pression et volume constants)

enthalpie massique de vaporisation de l'ammoniac à T₁=263K : L₁ =1,30.10³ kJ.kg^-1 ; enthalpie massique de vaporisation de l'ammoniac à T₃= 298 K : L₃ = 1,16.10³ kJ. kg^-1.