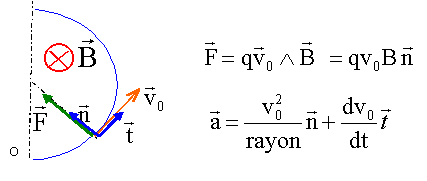|
|
||||
|
|
||||
|
||||
|
Un cyclotron sert à accélérer des particules chargées. Danc ce cas les particules sont des protons de masse m= 1,67 10-27 kg et de charge e= 1,6 10-19 C. Le cyclotron comporte deux demi cylindres conducteurs appelés "dees" et séparé par un intervalle étroit. Un champ magnétique uniforme B règne à l'intérieur de chaque "dee", sa direction est parallèle à l'axe des demi-cylindre, sa valeur est B= 1 T. Un champ électrique E variable dans le temps, peut être établi dans l'intervalle étroit qui sépare les "dees". Il permet d'augmenter la vitesse des protons chaque fois qu'il pénètrent dans cet intervalle. Ce champ électrique est obtenu en appliquant une tension sinusoïdale de valeur maximale Um= 2000 V et de fréquence f entre les deux "dees". 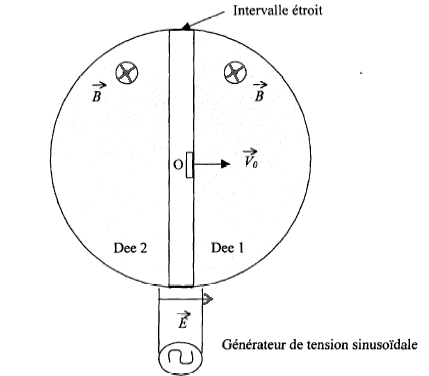
corrigé dans un dee : q : charge électrique en coulomb v : vitesse en m/s B : champ magnétique en tesla F : force de Lorentz en newton. La force magnétique est centripète, perpendiculaire au plan défini par la vitesse et le champ magnétique. Ecrire la seconde loi de Newton dans la base de Frenet :
l'accélération est centripète de norme qv0B/m = v0² /rayon en conséquence : dv/dt =0, le mouvement est uniforme ( norme de la vitesse constante) et qv0B = mv0² / rayon rayon = mv0 / (qB) le rayon est constant, le mouvement est circulaire. longueur L parcourue par un proton sur le demi-tour de rayon r0 : L= pr0 ( demi-circonférence) L= pmv0 / (qB) temps t mis par ce proton pour effectuer ce demi-tour à vitesse constante : t= L/v0 = pm / (qB), indépendant de v0. t= 3,14 * 1,67 10-27 / (1,6 10-19*1)= 3,28 10-8 s. Pour accélérer de manière efficace les particules : - d'une part la tension alternative doit être maximale : sa demi période est égale à la durée nécessaire pour effectuer ce demi tour. T= 2*t = 6,56 10-8 s ; fréquence f = 1/T = 1,53 107 Hz. - d'autre par le travail de la force électrique doit être positif : q Em >0 impose un changement du signe de la tension à chaque demi tour à la sortie : écrire le théorème de l'énergie cinétique : travail de la force électrique : qUm DEc = qUm = 1,6 10-19 * 2 103 = 3,2 10-16 J.à chaque ½ tour 3,2 10-16 / 1,6 10-19 = 2000 eV. la vitesse augmente à chaque fois que le proton traverse l'intervalle étroit ; or le rayon de la trajectoire est proportionnel à la vitesse ; donc le rayon augmente. nombre de tours : énergie finale de la particule divisée par l'énergie acquise à chaque tour v f= 2 107 m/s ; Ef= ½mvf² = 0,5*1,67 10-27 * (2 107)² = 3,34 10-13 J 3,34 10-13 / (2*3,2 10-16) = 522 tours. valeur du rayon à partir duquel les protons ayant acquis cette vitesse seront extraits r = mv/(qB) = 1,67 10-27 * 2 107 / 1,6 10-19 = 0,21 m.
|
||||
|
L'étude est menée à température constante de 298 K. Un film tensioactif disposé à la surface libre de l'eau est composé de molécules constituées de deux parties aux propriètès antagonistes: une partie hydrophile polaire, une partie hydrophobe. A l'interface eau/air, ces molécules forment spontanément une monocouche. La figure ci-dessous illustre ce comportement. Une barrière flotante PF sépare la cuve en deux compartiments, l'un contenant l'eau pure, l'autre l'eau recouverte du film. 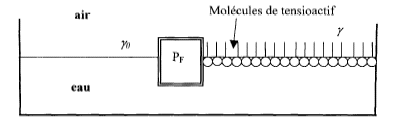
corrigé La partie hydrophile polaire est en contact avec l'eau. F= U-TS ; dF= dU - TdS à température constante or dU = d W
+ d Q ; dF= d W + d
Q-TdS la variation de F ( notée dF) est égale au travail dW reçu ou fourni par l'interface. F= gA ;
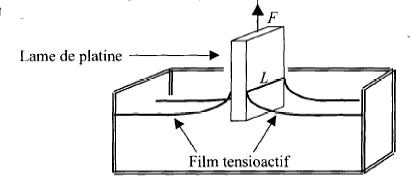
dF= gdA ; d W = gdA or le travail s'exprime en joule : joule = force * longueur = newton * mètre joule mètre -2 = newton * mètre *mètre -2 = newton * mètre-1.(une force par unité de longueur) Le rôle du tensioactif , dans ce cas, est de faciliter le passage des molécules d'eau dans l'air. Force FR par unité de longueur qui s'exerce sur la barrière flottante PF séparant les deux compartiments : FR= g0-g force tangente à l'interface liquide/air, dirigée vers l'eau sans tensioactif. Les gouttes de tensioactif ont modifié la tension superficielle de l'eau. La résultante des forces exercée par l'eau additionnée de tensioactif est inférieure à la résultante des forces exercée par l'eau pure. La lame de platine est soumise à : - son poids, vertical vers le bas, valeur mg - la force F, verticale vers le haut, valeur K I - la poussée d'Archimède , verticale vers le haut , valeur reau *g * volume de la lame immergé la tension superficielle, verticale vers le bas ( vers le liquide), valeur : g L de chaque coté de la lame soit 2g L à l'équilibre la somme vectorielle de ces forces est nulle : pour l'eau avec tensioactif : mg -KI +2g L =0 (1) pour l'eau pure : mg -KI0 + 2g0 L =0 (2) (1) donne : g = ( KI-mg) / (2L) (2) donne : mg = KI0 -2 g0 L ; repport ci-dessus : g = K(I-I0)/(2L)+ g0 g = g0 -K(I0-I)/(2L) I= 2,9 10-3A; I0 = 8,6 10-3 A ; L= 0,02 m ; K= 0,33 N/A ; g 0= 72 10-3 N/m g =72 10-3 - 0,33( 8,6-2,9) 10-3 / 0,04= 25 10-3 N/m.
|
||||
|
|