|
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
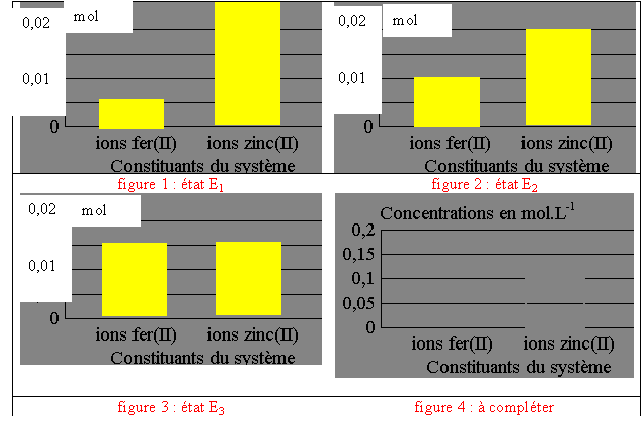
Certaines transformations chimiques peuvent mettre en jeu la réaction modélisée par l'équation (1): dont la constante d'équilibre associée est : K = 1,40 x 1011. on dispose : - d'une solution aqueuse de sulfate de fer S1 contenant des ions Fe2+(aq) de concentration 1,00.10-1 mol.L-1 . - d'une solution aqueuse de sulfate de zinc S2 contenant des ions Zn2+(aq) de concentration 1,00.10-1 mol.L-1 . Les données nécessaires à l'exploitation des expériences 1 et 2 sont rappelées ci-dessous : - les expériences sont réalisées à une température de 25°C; - on se limite aux couples oxydant/réducteur suivants : (Fe2+(aq)/Fe(s)) , (Zn2+(aq)/Zn(s)) ; et (H+(aq)/H2(g)); - masses molaires : M(Fe) = 55,6 g.mol-1 et M(Zn) = 65,4 g.mol-1 ; - nombre d'Avogadro : NA = 6,02.1023 mol-1 ; - charge élémentaire : e = 1,60.10-19 C. A ) Expérience 1 : Transformation spontanée A l'instant t = 0, on mélange dans un grand bécher 100 mL de la solution S1, 200 mL de la solution S2, 5,56 g de fer et 6,54 g de zinc, puis on agite. La transformation chimique de ce système peut être modélisée par l'équation (1).
B ) Expérience 2 : L'électrolyse : On réalise le montage représenté figure 5 (annexe). Le générateur de tension continue permet de faire circuler un courant électrique d'intensité I. 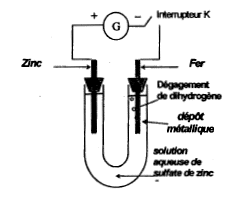
corrigé Fe2+(aq) +2e- = Fe(s) réduction Zn(s) = Zn 2+(aq) + 2e- oxydation Qté de matière (mol) = volume de la solution (L) * concentration (mol/L)= 0,1*0,1 = 10-2 mol ion Fe2+. 0,2*0,1 = 2 10-2 mol ion Zn2+. L'histogramme correspondant à l'état initial est celui de l'état E2. On retrouve les quantités de matière calculées. Fe2+(aq) + Zn(s) = Zn 2+(aq) + Fe(s) Qr,i= [Zn 2+]i/[Fe2+]i avec [Zn 2+]i= 2 10-2 /( 0,1+0,2) mol/L et [Fe 2+]i= 10-2 /( 0,1+0,2) mol/L Qr,i= 2 10-2 / 10-2 = 2. Si Qr < K, alors le système chimique évolue spontanément dans le sens direct ( vers la droite), si Qr = K, le système est dans l'état d'équilibre, sa composition n'évolue pas. si Qr > K, le système évolue spontanément dans le sens inverse (vers la gauche) Dans ce cas Qr < K ( 2 <1,4 1011) le système chimique évolue spontanément dans le sens direct état E1: n(Fe2+) = 0,005 mol et n(Zn2+) = 0,025 mol. (lecture graphe) Qr,1= [Zn 2+]1/[Fe2+]1=n(Zn2+) /n(Fe2+)= 0,025/0,005= 5. n(Fe2+) = n(Fe2+)i - x soit x = n(Fe2+)i - n(Fe2+) = 0,010 - 0,005 = 0,005 mol n(Zn2+) = n(Zn2+)i + x = 0,020 + 0,005 = 0,025 mol L'état E1 est donc à un état intermédiaire entre l'état initial et l'état final, avec l'avancement x=0,005 mol. état E3: n(Fe2+) = 0,015 mol et n(Zn2+) = 0,015 mol. (lecture graphe) Qr,3= [Zn 2+]3/[Fe2+]3=n(Zn2+) /n(Fe2+)= 0,015/0,015= 1. L'histogramme montre que n(Fe2+) a augmenté tandis que n(Zn2+) a diminué. cela correspond à l'évolution du système en sens inverse, en contradiction avec le critère d'évolution L'état E3 n'est donc pas un état intermédiaire entre l'état initial et l'état final.
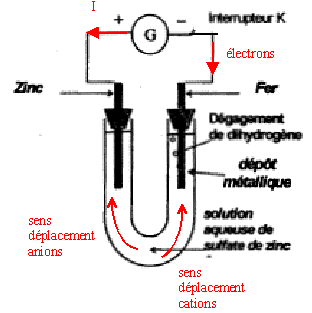
l'électrode de fer, où se produit des réductions est la cathode négative 2H+ + 2e-= H2(g) et Zn2+ + 2e- = Zn (s) Le dépôt de zinc protège le fer de la corrosion La masse de l'électrode de zinc diminue. Le zinc s'oxyde. Zn(s) = Zn2+(aq) + 2 e-. (anode soluble) à l'anode , oxydation : Zn (anode) = Zn2+(aq) + 2 e-. à la cathode, réduction : Zn2+(aq) + 2 e- = Zn (cathode) bilan : Znanode, (s) + Zn 2+(aq) = Zn 2+(aq) + Zncathode, (s) Quantité d'électricité (C) = intensité (A) * temps (s) = 0,5*10*60 = 300 C. Qté de matière d'électrons (mol) = 300 / ( NA e)= 300 / (6,02 1023*1,6 10-19)= 3,1 10-3 mol. n(Zn)= ½ne = 1,55 10-3 mol de zinc disparu soit en masse (g) = masse molaire zinc (g/mol) * Qté de matière (mol) = 65,4 *1,55 10-3 = 0,10 g.
|
||||||||||||||||||||||||
|
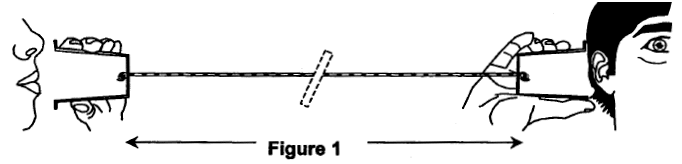
A l'ère du téléphone portable, il est encore possible de communiquer avec un système bien plus archaïque… L'onde sonore produite par le premier interlocuteur fait vibrer le fond du pot de yaourt, le mouvement de va et vient de celui-ci, imperceptible à l'œil, crée une perturbation qui se propage le long du fil. Cette perturbation fait vibrer le fond du second pot de yaourt et l'énergie véhiculée par le fil peut être ainsi restituée sous la forme d'une onde sonore perceptible par un second protagoniste. Données : célérité du son dans l'air à 25°C vair = 340 m.s-1 A ) A propos des ondes :
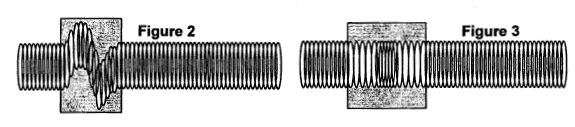
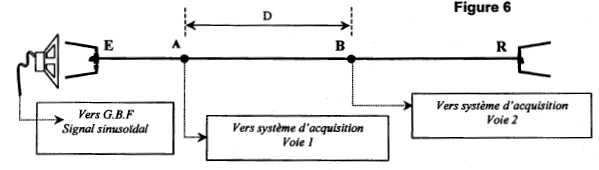
B ) Célérité de l'onde qui se propage le long du fil : A 25°C, on réalise le montage suivant (figure 4), afin de mesurer la célérité des ondes sur le fil du dispositif. Deux capteurs, reliés en deux points A et B distants de D = 20 m sur le fil, détectent successivement le passage d'une perturbation générée par un son bref à l'entrée du pot de yaourt émetteur E.
corrigé L'onde sonore se propage en premier dans l'air, ensuite dans le fond du 1er pot de yaourt, dans le fil, dans le fond du 2ème pot de yaourt et enfin dans l'air. Figure 2 : Onde transversale, la direction de la perturbation (ici la verticale) est perpendiculaire à la direction de propagation de l'onde. (ici l'horizontale). Figure 3: Onde
longitudinale, la direction de la perturbation et la direction de
propagation de l'onde sont identiques.
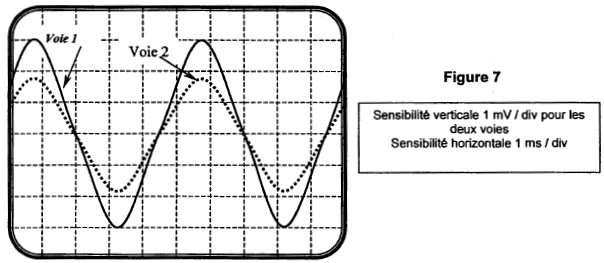
célérité (m/s) = distance (m) / durée (s) =D/ t= 20 / 0,02 = 1000 m/s. Cette valeur est bien supérieure à la célérité du son dans l'air : une onde se propage plus rapidement dans un solide que dans un gaz. [µ] = [M].[L]-1 ; [k] = [M].[T]-2 ; [k.L] = [M].[T]-2.[L] [µ] [k.L]-1= [M].[L]-1[M]-1.[T]2.[L]-1=[T]2 [L]-2 [µ]½ [k.L]-½ =[T] [L]-1 expression (1) non retenue l'expression (2) est l'inverse de l'expression (1) : l'expression (2) correspondant à une vitesse est retenue. l'expression (3) est l'expression (2) élevée au carrée, soit une vitesse au carrée. v= (20*50/10-3)½=1000 m/s.
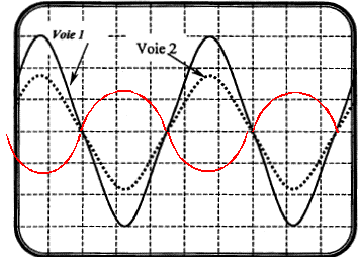
L'onde s'amortit durant sa propagation dans le milieu. L'amplitude de la perturbation diminue lorsqu'on s'éloigne de la source (émetteur) période : 5 divisions soit 5 *10-3 = 5 10-3 s fréquence f = 1/5 10-3 = 200 Hz. Les signaux se retrouvent dans le même état lorsque D = n.l avec n entier. en conséquence l = 5 m. célérité de l'onde : v (m/s) = l f = 5*200 = 1000 m/s. Si D = 27,5 m, D =(2n+1) ½l avec n = 5. Les deux signaux sont en opposition de phase à chaque instant. Le signal de la voie 2 possède une amplitude plus faible (amortissement )
Dans un milieu dispersif, la célérité de l'onde dépend de sa fréquence. Si le fil était un milieu dispersif, les ondes de basses fréquences ( sons graves) se propageraient avec une célérité différente des ondes de hautes fréquences (sons aigus). Si le milieu était dispersif , le téléphone pot de yaourt ne pourrait pas marcher correctement. Les ondes électromagnétiques se propagent dans le vide contrairement aux ondes mécaniques qui nécessitent l'existence d'un milieu matériel.
|
|||||||||||||||||||||||||
|
La grêle se forme dans les cumulo-nimbus situés entre 1 000 m et 10 000 m d'altitude où la température est très basse, jusqu'à – 40°C. Le grêlon tombe lorsqu'il n'est plus maintenu au sein du nuage. Au sol sa vitesse peut atteindre 160 km/h. On étudie un grêlon de masse 13 g qui tombe d'un point O d'altitude 1 500 m sans vitesse initiale. Il peut être assimilé à une sphère de diamètre 3,0 cm. Le point O sera pris comme origine d'un axe Oz orienté positivement vers le bas. L'intensité de la pesanteur sera considérée comme constante et de valeur g0 = 9,80 m.s-2 . Données : volume d'une sphère V = 4/3 p.r3 ; masse volumique de l'air r = 1,3 kg.m-3 . A ) Chute libre : On admettra que le grêlon tombe en chute libre.
B ) Chute réelle : En réalité le grêlon est soumis à deux autres forces, la poussée d'Archimède FA et la force de frottement fluide F proportionnelle au carré de la vitesse telle que F = K.v2 .
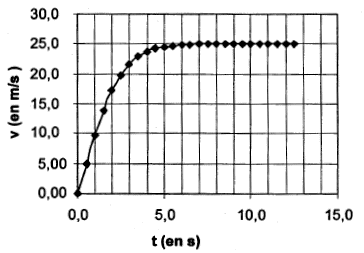 Retrouver graphiquement la valeur de la vitesse calculée au paragraphe précédent.
corrigé On applique la deuxième loi de Newton au grêlon dans le référentiel terrestre supposé galiléen ; on choisi un axe vertical orienté vers le bas, origine : le point de départ O. en chute libre, le poids est la seule force appliquée : ma = mg d'où a=g. la vitesse est une primitive de l'accélération : v= gt ( vitesse initiale nulle) la position est une primitive de la vitesse : z= ½gt².( position initiale prise comme origine) au sol z = 1500 m ; t²= 3000/g ; t = [3000/g]½. repport dans l'expression de la vitesse : v = g[3000/g]½ = [3000*g]½ = [3000*9,8]½ = 171,5 m/s=617 km/h. cette valeur est
bien trop grande pour correspondre à la réalité , ainsi qu'à la valeur
proposée dans le texte; on a négligé les forces de frottements sur les
couches d'air.
vitesse ² = longueur ² / temps² soit [L]2[T]-2 ; K= F/v² soit [M][L][T]-2 [L]-2[T]2 = [M][L]-1 L'unité du coefficient K dans le Système International est donc kg.m-1. Poussée d'Archimède = poids du volume de fluide (air) déplacé = volume grêlon * rair*g FA= 4/3 p.r3 rairg avec r = 1,5 10-2 m. FA= 4/3*3,14*(1,5 10-2)3*1,3*9,8 = 1,8 10-4 N. poids P=mg= 0,013*9,8 = 0,13 N La poussée d'Archimède est négligeable devant le poids du grêlon.
Le grêlon est soumis à son poids, vertical vers le bas et à la force de frottement verticale vers le haut mg - Kv² = ma = m dv/dt soit dv/dt = g-K/mv². A = g et B= K/m. On utilise l'équation différentielle pour déterminer a4 : a4 = 9,8-1,56 10-2 v42 avec v4 = 17,2 m/s. a4 = 9,8-1,56 10-2* 17,22 = 5,18 m/s². Dans la méthode d'Euler, on utilise l'approximation suivante : a = Dv / D t. Dv = v5-v4= a4D t soit v5= v4+ a4D t v5= 17,2 + 5,18 * 0,5 = 19,8 m/s. Lorsque la vitesse limite est atteinte par le grêlon, la vitesse est constante, l'accélération a est alors nulle. 0= A-Bvl2 soit vl =(A/B)½= (9,8/1,56 10-2)½=25,1 m/s. D'après la courbe, l'asymptote horizontale donne la valeur de la vitesse limite, valeur en accord avec celle calculée ci-dessus..
|
|||||||||||||||||||||||||
|
|