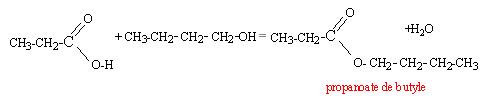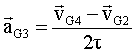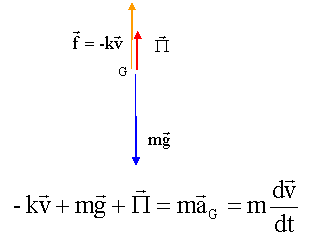Aurélie avril 05

propriétés de l'acide propanoïque ; circuit RL

mouvement d'un palet d'après bac Pondichéry 2005- d'après "Labolycée"





Google



propriétés de l'acide propanoïque : 6,5 points .

Données :

formule brute
masse volumique kg m-3
masse molaire g/mol
température ébullition °C
acide propanoïque
C3H6O2
1000
74
141
butan-1-ol
C4H10O
810
74
117,5
ester


146
eau


100
L'acide propanoïque est noté AH et l'ion propanoate A-. On considère une solution aqueuse d'acide propanoïque. On néglige la concentration en ion HO- par rapport à celle s des autres espèces ainsi que leur contribution à la conductivité de la solution.

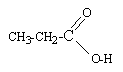
La conductivité de la solution est de la forme : s= l 1[H3O+] +l 2 [A-] avec l 1=35 10-3 S m² mol-1 et l2 =3,58 10-3 S m² mol-1 à 25°C.

I étude de la réaction ente l'acide propanoïque et l'eau :

On verse 0,1 mole d'acide propanoïque pur dans de l'eau pour obtenir 500 mL d'une solution notée S0. On souhaite obtenir V= 1 L de solution S de concentration 2 10-3 mol/L.

  1. Indiquer le protocol à suivre pour obtenir la solution S à partir de S0.
  2. Ecrire la formule semi-développée de l'acide propanoïque.
  3. Dresser un tableau d'avancement de la tranformation de 2 10-3 mol d'acide propanoïque dans un volume d'eau tel qu'on obtient V= 1,00 L de la solution S.
  4. Etablir la relation entre la conductivité s de la solution, l 1, l 2 , le volume V et l'avancement à l'équilibre.
  5. La mesure de la conductivité donne 6,2 10-3 S/m. Déterminer l'avancement à l'équilibre ; en déduire [H3O+]éq, [A-] éq et [AH] éq.
  6. Rappeler l'expression de la constante d'acidité Ka du couple acide propanoïque / ion propanoate et la calculer. En déduire le pKa du couple.

II étude de la réaction ente l'acide propanoïque et un alcool :

On prélève 0,20 mole d'acide propanoïque pur et 0,20 mole de butan-1-ol pur que l'on verse dans un ballon.

  1. Comment s'appelle la réaction qui a lieu entre les deux réactifs ? Ecrire l'équation de cette réaction chimique. On pourra utiliser les formules brutes.
  2. Donner le nom des produits formés et leurs formules semi-développées.
  3. Dresser le tableau d'avancement de la transformation. En déduire l'expression du quotient de réaction Qr en fonction de l'avancement x à la date t.
  4. Calculer l'avancement à l'équilibre sachant que la constante de réaction K= 4.
  5. En déduire le taux d'avancement final t.
  6. On demande à un groupe d'élèves de formuler des propositions pour augmenter le taux d'avancement final. On relève les propositions suivantes :
    1 : on chauffe le milieu réactionnel.
    2 : on ajoute un catalyseur : l'acide sulfurique concentré par exemple.
    3 : on réalise une distillation pour éliminer l'eau.
    4 : on chauffe à reflux
    Choisir la proposition qui vous semble correct en justifiant. Quel montage réaliserez vous parmi xeux exposés ci-dessous ?

 

corrigé
concentration solution mère : Qté de matière (mol) / volume solution (L) = 0,1/0,5 = 0,2 mol/L

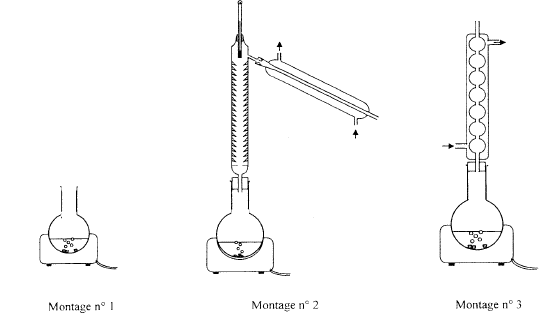
facteur de dilution = concentration mère / concentration fille = 0,2 / 2 10-3 = 100

prélever 10 mL de la solution mère à l'aide d'une pipette jaugée + pipeteur

placer dans une fiole jaugée de 1 L contenant un peu d'eau distillée

compléter avec de l'eau distillée jusqu'au trait de jauge

agiter pour rendre homogène

AH + H2O = A- + H3O+

AH
+ H2O
= A-
+ H3O+
initial
2 10-3 mol
solvant en grande quantité
0
0
en cours
2 10-3 -x
x
x
final
2 10-3 -xéqui
xéqui
xéqui
volume de la solution 10-3 V m3 ; s= l 1[H3O+] +l 2 [A-]

s=( l 1+l 2 )xéqui / (10-3 V)= 103( l 1+l 2 )xéqui /V.

xéqui = s V / (103( l 1+l 2 ))=6,2 10-3 / (103*38,58 10-3)= 1,61 10-4 mol.

[A-] éq= [H3O+]éq= 1,61 10-4 mol./L [A-] éq ; [AH] éq= (2 10-3 -1,61 10-4 )/ 1 = 1,84 10-3 mol/L

Ka =[A-] éq[H3O+]éq /[AH] éq= (1,61 10-4)² / 1,84 10-3 = 1,41 10-5.

pKa = - log Ka = - log 1,41 10-5= 4,85.

estérification
AH
+alcool
= ester
+ eau
initial
0,2 mol
0,2 mol
0
0
en cours
0,2-x
0,2-x
x
x
final
0,2-xéqui
0,2-xéqui
xéqui
xéqui
Qr = [ester] [eau]/ ([alcool][acide]) = x²/(0,2-x)²

K = Qr, équi = [ester]équi [eau]équi/ ([alcool]équi[acide]équi)

K= xéqui² / (0,2-xéqui)² = 4

xéqui / (0,2-xéqui) = 2 ; xéqui = 2(0,2-xéqui)=0,4-2xéqui ; xéqui =0,4/3 = 0,133 mol

t = xéqui / xmax =0,133 / 0,2 = 0,667.

1 et 2 et 4 permettent d'atteindre plus rapidement l'équilibre sans en modifier la composition.

3 déplace l'équilibre dans le sens direct,( t augmente) car on élimine l'un des produits au fur et à mesure qu'il se forme.

montage de distillation fractionnée n°2.


circuit RL (4 points)

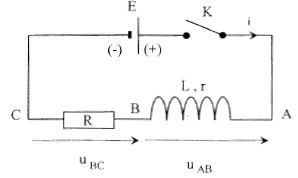
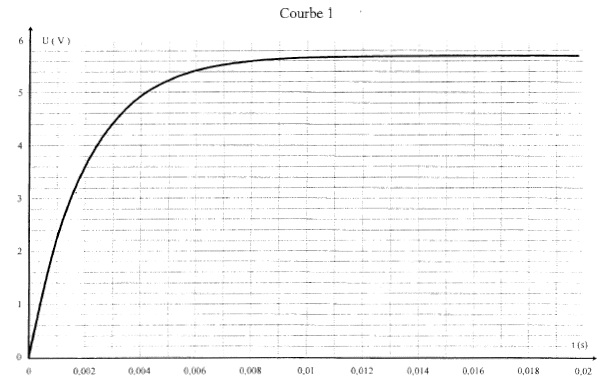
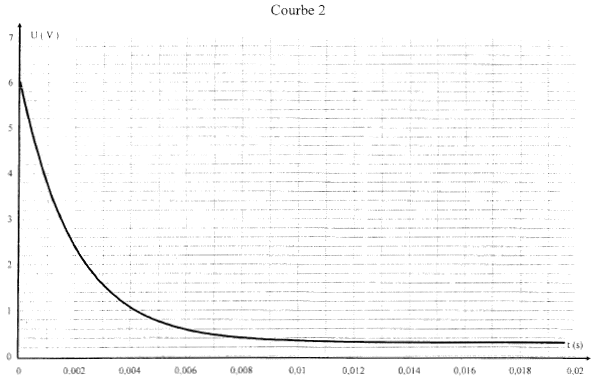
E= 6,00 V ; R= 200 W; r = 10,0 W.

Un ordinateur relié par une interface appropriée permet de visualiser au cours du temps les tensions uAB et uBC. A t=0, on ferme l'interrupteur K et on procède à l'acquisition. On obtient les deux courbes suivantes :

 

  1. Etude du montage :
    - A défaut d'ordinateur et d'interface, quel type d'appareil peut-on utiliser pour visualiser le phénomène étudié ?
    - Donner l'expression de uAB en fonction de i et di/dt.
    - Donner l'expression de uBC en fonction de i.
    - Associer les courbes ci-desus aux tensions uAB et uBC.
  2. Intensité du courant en régime permanent :
    - Déterminer I0 l'intensité du courant en régime permanent et donner sa valeur en exploitant l'une des courbes.
  3. Calcul de l'inductance :
    - Exploiter l'une des deux courbes pour déterminer la constante de temps t du montage. Expliciter votre méthode.
    - Rappeler l'expression de la constante de temps en fonction des grandeurs caractéristiques du circuit. Montrer que cette expression est homogène à un temps.
    - A partir de la valeur de t mesurée, calculer l'inductance L de la bobine.

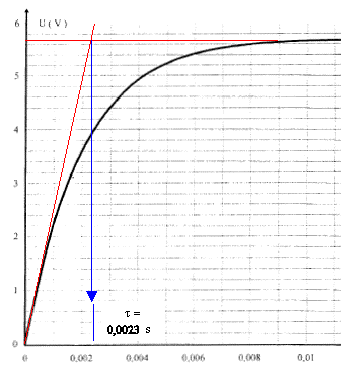
corrigé
oscilloscope à mémoire

uAB = Ldi/dt + r i ; uBC = R i

courbe 1 associée à uBC : uBC est proportionnelle à l'intensité du courant i

la courbe 1 montre un retard à l'établissement du courant dû au phénomène d'auto-induction.

courbe 1 associée à uAB : la tension aux bornes de la bobine diminue au cours du temps car di/dt diminue ; cette tension est égale à ri en régime permanent.

en régime permanent : uAB = rI0 ; uBC = R I0 ; uAC = E

uAB + uBC = uAC

rI0 + R I0 =E ; I0 = E / (R+r) = 6/ 210 = 0,028 A

à partir de la courbe 1, l'asymptote horizontale donne uBC= 5,7 V = R I0 avec R = 200 W.

I0 = 5,7 / 200 = 0,028 A.

t = L/ (R+r)

R+ r : tension / intensité soit V A-1 ;

u = Ldi/dt soit L = u dt / di : tension temps / intensité soit V s A-1.

L/ (R+r) : seconde.

t = L/ (R+r) ; L= t (R+r) = 0,0023* 210 = 0,483 H.

mouvement d'un palet ( 5,5 points)

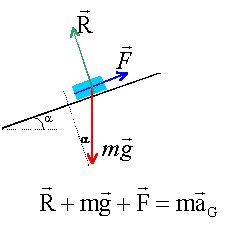
Les trois parties sont indépendantes.

Un palet en acier de masse m = 50,0 g peut se déplacer dans une gouttière inclinée d'un angle a= 28,0° avec l'horizontale. En D, le palet pase avec une vitesse vD acquise à l'aide d'un propulseur à ressort. En F, la gouttière est ouverte et le palet peut sortir librement. Il tombe ensuite dans une éprouvette contenant de la glycérine. Les frottements sont négligeables dans les parties 1 et 2, lorsque le palet glisse sur la gourrière. g= 9,80 m/s².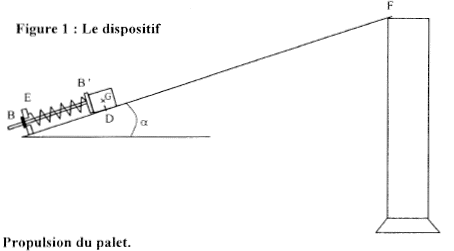

Partie I : propulsion du palet :

Dans le bas de la gouttière se trouve un dispositif de propulsion constitué d'une tige munie de deux butées B et B' servant d'axe à un ressort. Le dispositif a une masse négligeable devant celle du palet. Le ressort a une longueur à vide l0.

L'extrémité E du ressort est maintenue fixe, l'autre est libre et reste en contact avec le palet par l'intermédiaire de la butée B', tant que le ressort est comprimé.

La position du centre d'inertie G du palet est repérée sur un axe x'x de même direction que la ligne de plus grande pente de la gouttière et orienté vers le haut.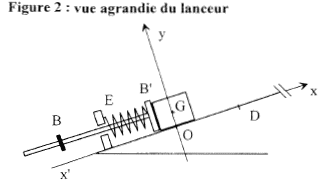

Un manipulateur tire sur la tige et comprime le ressort jusqu'à ce que le centre d'inertie du palet se trouve en O. En lâchant la tige, il libère le dispositif qui propulse le palet. Lorsque le centre d'inertie du palet arrive en D, la butée B bloque le mouvement du ressort qui retrouve dans cette position sa longueur à vide et libère le palet. On film le mouvement du palet puis on exploite la vidéo par un logiciel approprié. La figure ci-dessous représente la position qu'occupe le centre d'inertie G du palet à intervalles de temps réguliers t = 20,0 ms. A t=0, le centre d'inertie du palet est en O ou G0.

  1. En exploitant le document, déterminer les vitesses vG2 et vG4 du palet aux points G2 et G4.
  2. Exprimer le vecteur accélération du palet au point G3 en fonction des vecteurs vitesses aux points G2 et G4. En déduire la valeur de cette accélération aG3.
  3. Faire l'inventaire des forces qui agissent sur le palet et les représenter sur un schéma.
  4. En projetant la seconde loi de Newton appliquée au palet sur l'axe x'x ,exprimer la valeur de la force de rappel F du ressort en fonction de m, g, aG et a.
  5. Calculer la valeur de F au point G3.

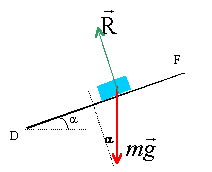
Partie II : montée du palet dans la gouttière:

Le palet n'est plus sous l'action du propulseur et il quitte le point D avec la vitesse vD= 2 m/s, puis il glisse jusqu'au point F où il s'arrête. dans cette partie , on prend le point D comme origine das altitudes et comme le niveau de référence de l'énergie potentielle de pesanteur.

  1. Faire l'inventaire des forces qui s'appliquent au palet sur le trajet DF et les représenter sur un schéma.
  2. Donner lexpression au point D de l'énergie mécanique EM(D) du palet en translation dans le champ de pesanteur.
  3. Donner lexpression au point F de l'énergie mécanique EM(F) en fonction de m, g, DF et a.
  4. Montrer que sur le trajet DF, l'énergie mécanique du palet en translation dans le champ de pesanteur se conserve. En déduire la valeur de DF.

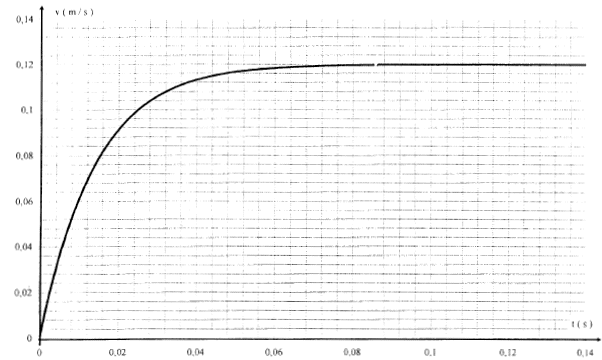
Partie III : chute du palet sans vitesse initiale :

En F, le palet poursuit son mouvement en réalisant une chute verticale ( sans vitesse initiale) dans une éprouvette contenant de la glycérine. On admettra, dans ce cas que le palet est soumis à une force de frottement fluide, modélisée par un vecteur f colinéaire à la vitesse mais de sens contraire et de valeur f= k v où k est une constante positive.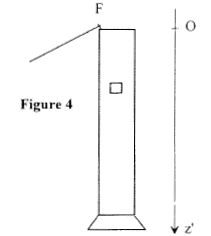

  1. Faire l'inventaire des forces qui agissent sur le palet pendant sa chute dans la glycérine et faire un schéma.
  2. En appliquant la seconde loi de Newton, montrer que le mouvement du centre d'inertie du palet obéit à une équation différentielle du type : dv/dt = A- Bv. Donner les expressions littérales de A et B en fonction des données du texte, de la masse volumique r de la glycérine et du volume Vpalet du palet.
  3. En utilisant le graphe ci-dessous calculer numériquement A et B en justifiant votre démarche.
 

corrigé
vG2 = G1G3/(2t) = 4,9 10-2 / 4 10-2 = 1,22 m/s.

vG4 = G3G5/(2t) = 6,5 10-2 / 4 10-2 = 1,62 m/s.

les vecteurs étant colinéaires : aG3 =( vG4-vG2)/(2t)= (1,62-1,22) / (4 10-2 )= 10 m/s².

le palet est soumis à son poids , à l'action de la gouttière et à l'action du ressort comprimé.

projection sur l'axe x'x : -mg sin a +F = maG soit F= maG + mg sin a.

au point G3 : F=0,05 ( 10+ 9,8*sin 28) = 0,73 N.

EM(D)= ½mv²D ; EM(F)= m g DF sin a.

La force R, perpendiculaire à la vitesse ne travaille pas ; seul le poids travaille sur le trajet DF et en conséquence l'énergie mécanique du palet se conserve.

½mv²D= m g DF sin a.

DF= 0,5 v²D/ ( g sin a)= 0,5 * 2² / (9,8 sin 28)= 0,435 m.

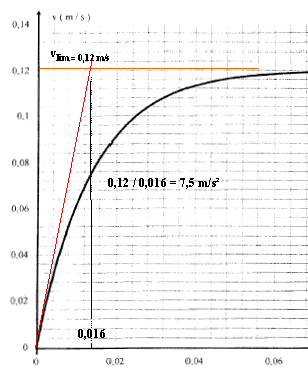
la poussée d'Archimède a pour valeur P = Vpalet r g.

projection sur l'axe verticale descendant : -kv + mg - Vpalet r g= m dv/dt

diviser par m : dv/dt = g(1-Vpalet r/m)- k/m v .

A = g(1-Vpalet r/m) ; B = k/m

Quand le mouvement devient uniforme, dvlim /dt = 0 soit A-B vlim=0

vlim= A/B = 0,12 m/s ( lecture graphe)

à t=0, la vitesse est nulle : dv/dt ( t=0 )= A (coefficient directeur de la tangente à l'origine) = 7,5 m/s².

B= A/0,12 = 7,5 / 0,12 = 62,5 s-1.

retour -menu