|
dipôle (RL) ; cinétique de la saponification de l'éthanoate d'éthyle |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Les parties A et B sont indépendantes. Dans tout ce qui suit, les frottements sont négligés. Partie A : pendule simple. On étudie un pendule simple constitué d'une masse ponctuelle m, attachée à l'une des extrémités d'un fil inextensible, de masse négligeable et de longueur L. Ce pendule est placé dans le champ de pesanteur dans le référentiel terrestre considéré comme galiléen. 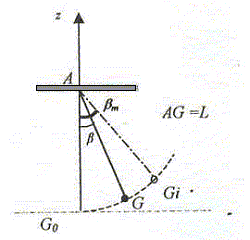 L'autre extrémité du fil est attachée en un point fixe A. Écarté de sa position d'équilibre G0, le pendule oscille sans frottements avec une amplitude bm. Gi est la position initiale à partir de laquelle le pendule est abandonné sans vitesse. Une position quelconque G est repérée par b , élongation angulaire mesurée à partir de la position d'équilibre.
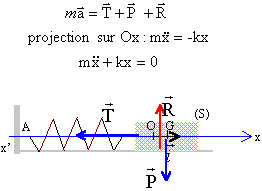
 Partie B : oscillateur élastique. Un solide (S) de masse m, de centre d'inertie G, peut glisser sans frottements sur une tige horizontale. Il est accroché à un ressort (R) à spires non jointives, de raideur k = 4,0 N.m-1. L'ensemble constitue un oscillateur élastique horizontal, non amorti. La masse du ressort est négligeable devant m et (S) entoure la tige de telle sorte que G se trouve sur l'axe de celle-ci. 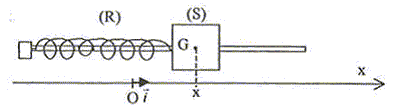 On étudie le mouvement de translation du solide (S) dans le référentiel terrestre supposé galiléen. Lorsque le solide (S) est à l'équilibre, son centre d'inertie G se situe à la verticale du point O, origine de l'axe des abscisses. Le solide est écarté de 10 cm de sa position d'équilibre et abandonné sans vitesse initiale à la date t = 0 s. On procède à l'enregistrement des positions successives de G au cours du temps par un dispositif approprié. On obtient la courbe ci-dessous : 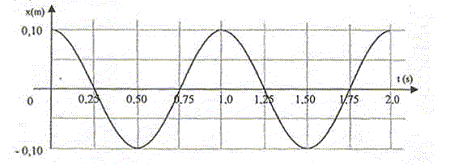
Partie C : comparaison des périodes.
corrigé énergie cinétique en G : Ec= ½mv² ( masse m en kg ; vitesse v en m/s ; énergie en joule J) expression de l'énergie mécanique, somme des énergies cinétique et potentielle. E= Ec+Ep = ½mv² + mgL(1 - cosb ) En absence de frottements, l'énergie mécanique se conserve. ou bien, seul le poids travaille, la tension du fil étant perpendiculaire à la vitesse : en conséquence l'énergie mécanique se conserve. vitesse au passage par la position d'équilibre : Au départ en Gi, l'énergie mécanique est sous forme potentielle de pesanteur : mgL(1 - cosbm ) Au pasage en G0, l'énergie est sous forme cinétique et la vitesse est maximale vmax : ½mv²max. L'énergie mécanique se conserve : mgL(1 - cosbm ) = ½mv²max. gL(1 - cosbm ) = ½v²max ; v²max =2gL(1 - cosbm ) ; vmax = (2gL(1 - cosbm ))½. vmax = (20(1 - 0,95 ))½= (20*0,05)½= 1 m/s. loi d'isochronisme des petites oscillations : Lorsqu’on écarte un pendule simple de sa position d’équilibre d’une abscisse angulaire bm et qu’on l’abandonne à lui même,on constate que, pour des valeurs de bm n’excédant pas une dizaine de degrés, celui-ci effectue des oscillations libres dont la période T est indépendante de bm. On dit que le pendule simple vérifie la loi d’isochronisme des petites oscillations. analyse dimensionnelle : le second membre doit être homogène à un temps. 2p est sans dimension. g : accélération en m/s² : longueur / temps² soit[g]= LT² ; L : longueur en mètre g/L : 1/temps ² soit [g/L]=T-2 ; [racine carrée (g/L)] =T-1 La première expression est fausse ; mais on peut en déduire
que la troisième expression est exacte car [racine carrée (L/g)] =T.
l'équation différentielle m x"+ kx=0 s'écrit : x"+k/m x=0 ou encore x"+w²x=0 avec w ²=k/m Or w = 2p/T0 soit T0 = 2p/ w = 2p racine carrée (m/k). Expression littérale de l'énergie mécanique du système {ressort + solide} énergie cinétique : Ec=½mv² avec v=x' ; Ec=½mx'² énergie potentielle élastique : Ep=½kx² énergie mécanique : E=½mx'²+½kx². L'énergie potentielle élastique du système {ressort + solide} est maximale lorsque x=Xm soit aux dates : 0, 1, 2 s. Lénergie cinétique est nulle à ces mêmes dates ( la tangente à la courbe à ces dates est horizontale : donc x'=0) Valeur de l'énergie mécanique du système : en absence de frottement l'énergie mécanique du système se conserve ; il suffit de calculer l'énergie mécanique initiale à t=0, celle-ci se trouve sous forme potentielle élastique : E= ½kX²m = 0,5*4*0,01 = 0,020 J= 20 mJ. Sur la Lune glune est environ 6 fois plus petit que gterre. La masse est constante. la période du pendule est proportionnelle à g-½ : donc si g diminue, la période augmente. La période de l'oscillateur élastique est indépendante de g ; de plus la masse est constante ; la raideur est une caractéristique du ressort. La période de l'oscillateur élastique ne change pas.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
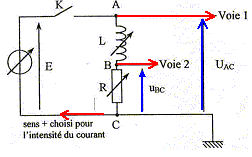
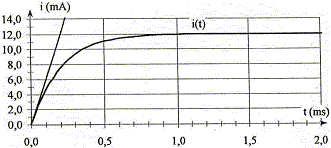
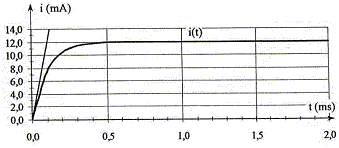
On se propose d'étudier l'établissement du courant dans un dipôle comportant une bobine et un conducteur ohmique lorsque celui-ci est soumis à un échelon de tension de valeur E. Le conducteur ohmique a une résistance R. La bobine sans noyau de fer doux, a une inductance L ; sa résistance r est négligeable devant R. Les valeurs de E, R, L sont réglables. On dispose d'un système d'acquisition de données et d'un logiciel adapté pour le traitement des données. On réalise le montage ci-contre :
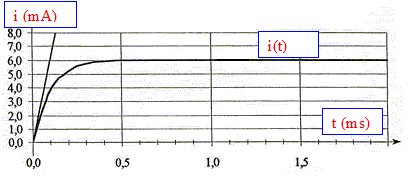
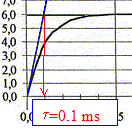
corrigé La tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles Pour suivre l'évolution de l'intensité i du courant en fonction du temps, on suit l'évolution de la tension uBC aux bornes du résistor R. On doit ensuite diviser cette tension uBC par R= 1 kW pour avoir l'image de l'intensité en mA. valeur I de l'intensité du courant en régime permanent : ordonnée de l'asymptote horizontale. I= 6,0 mA. constante de temps t du dipôle RL : abscisse de l'intersection de l'asymptote horizontale avec la tangente à l'origine valeur théorique : t= L/R= 0,1 /
1000 =1,0 10-4
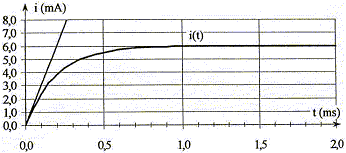
s accord entre valeurs expérimentale et théorique. équation différentielle vérifiée par l'intensité du courant i(t) : additivité des tensions E= UAB + UBC avec UAB = Ldi/dt = Li' et UBC = Ri d'où E= Li'+Ri. En régime permanent dI/dt=I' =0 d'où E = RI soit I= E/R = 6 / 1000 = 0,006A =6,0 mA. graphe 2 : I= 6 mA ; or I= E/R d'où expérience D de plus t= 0,2 ms ; or t = L/R : si R inchangée, L doit doubler donc expérience D. graphe 3 : I= 12 mA ; or I= E/R d'où expériences B ou C de plus t= 0,2 ms ; or t = L/R : si L inchangée, R doit être divisée par deux donc expérience C. graphe 4 : I= 12 mA ; or I= E/R d'où expériences B ou C de plus t= 0,1 ms ; or t = L/R : si L inchangée, R doit être inchangée donc expérience B.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
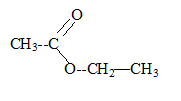
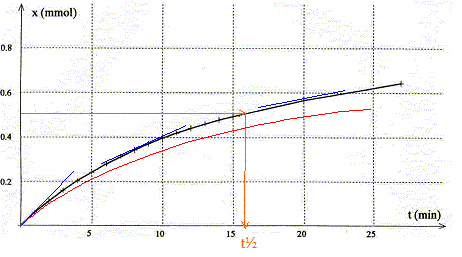
corrigé l'éthanoate d'éthyle appartient à la famille des esters.
espèce chimique A- : ion éthanoate CH3-COO-. La réaction de saponification est lente, mais totale.
Du point de vue de la conductivité, tout se passe comme si on remplaçait l'ion HO-(aq) par l'ion A-(aq) dont la conductivité molaire ionique est cinq fois plus petite : en conséquence, au cours du temps, la conductivité de la solution diminue. st = lNa+ [Na+] + lHO- [HO-] + lA- [A-] st = lNa+ c0 + lHO- (c0-x(t)/V) + lA- x(t)/V à l'instant t = 0 , [A-] =0 donc s0 = (lNa+
+lHO- ).c0 ; au bout
d'une durée très grande, [HO-] =0; [A-] = c0
( réaction totale) donc soo,
= ( lNa+ + lA-
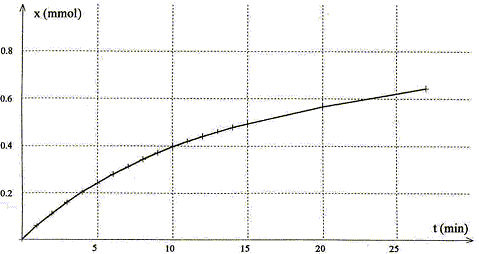
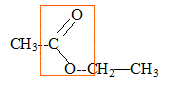
).c0 . s0-st= lHO-x(t)/V- lA- x(t)/V = (lHO--lA-)x(t)/V s0- soo= lNa+ c0 +lHO- c0-lNa+ c0 - lA- c0=lHO- c0- lA- c0 = (lHO-- lA-)c0 s0-st/ (s0- soo)=x(t) / (Vc0) d'où x(t) = c0V(s0-st) / (s0- soo) expression de la vitesse volumique de réaction : 1/V dx(t) / dt d'après le graphe x(t) en mmol, t en minute, V en L d'où l'unité de la vitesse : mmol min-1 L-1. méthode permettant d'évaluer graphiquement cette vitesse à un instant donné : tracer la tangente à la courbe x(t) = f( t) à une date donnée; déterminer le coefficient directeur de la tangente: celui-ci est égal à dx/dt; puis diviser par le volume de la solution V= 0,1 L. Cette vitesse diminue au cours de la transformation chimique ( la tangente à la courbe se rapproche de l'horizontale) du fait de la diminution des concentrations des réactifs. xmax = c0V= 0,01*0,1 = 0,001 mol = 1 mmol. Le temps de demi-réaction est la durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final ( dans ce cas 1 mmol) x(t½) = 0,5 mmol Le graphe donne t½=16 min. La température est un facteur cinétique : à 20°C la vitesse est à chaque instant inférieure à la valeur de celle-ci à 30°C. La valeur de t½ à 20°C est plus grande que la valeur trouvée ci-dessus.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||