|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Cet exercice est un questionnaire à réponses ouvertes courtes. A chaque question peuvent corres-pondre aucune, une ou plusieurs propositions exactes. Pour chacune des questions, plusieurs réponses ou affirmations sont proposées. Inscrire en toutes lettres " vrai " ou " faux " et donner une justification ou une explication. Une réponse fausse ou une absence de réponse sera évaluée de la même façon. Les parties 1, 2, 3 et 4 sont indépendantes et peuvent être traitées séparément. 1. Ondes infrasonores. Les éléphants émettent des infrasons (dont la fréquence est inférieure à 20 Hz). Cela leur permet de communiquer sur de longues distances et de se rassembler. Un éléphant est sur le bord d'une étendue d'eau et désire indiquer à d'autres éléphants sa présence. Pour cela, il émet un infrason. Un autre éléphant, situé à une distance L = 24,0 km, reçoit l'onde au bout d'une durée Dt = 70,6 s. La valeur de la célérité de l'infrason dans l'air v est : 34,0 km.s-1 ; 340 km.s-1 ; 340 m.s-1 . célérité (m/s) = distance (m) / durée (s) = 24000/70,6 = 340 m.s-1 2. Ondes à la surface de l'eau Au laboratoire, on dispose d'une cuve à onde contenant de
l'eau immobile à la surface de laquelle flotte un petit morceau de
polystyrène. On laisse tomber une goutte d'eau au-dessus de la cuve, à
l'écart du morceau de polystyrène. Une onde se propage à la surface de
l'eau. onde mécanique transversale : pour se propager l'onde à besoin d'un milieu dont l'une des propriiétés est modofiée. La déformation du milieu, verticale, est perpendiculaire à la direction de propagation de l'onde. - L'onde atteint le morceau de polystyrène. Celui-ci se déplace parallèlement à la direction de propagation de l'onde ; faux ( l'onde ne transporte pas de matière mais de l'énergie) Celui-ci se déplace perpendiculairement à la direction de propagation de l'onde ; vrai Celui-ci monte et descend verticalement ; vrai Celui-ci reste immobile. faux 3. Ondes le long d'une corde L'extrémité gauche d'une corde est reliée à un vibreur effectuant des oscillations sinusoïdales entretenues à partir d'un instant de date t0 = 0 s. Les graphiques 1 et 2 représentent l'état de la corde à une date donnée. Les élongations y et les abscisses x sont graduées en cm. On néglige tout amortissement dans la totalité des questions de cette partie 3. 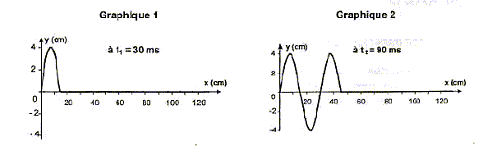
- Le graphique 2 ci-dessus permet de déterminer la valeur numérique de la longueur d'onde l. On trouve : 20 cm ; 30 cm ( lecture graphe 2 entre deux sommets consécutifs : la longueur d'onde est la période spatiale); 46 cm . - À partir des graphiques 1 et 2, déterminer la valeur de la période temporelle T : 30 ms ; 60 ms ; 18 ms . T= t2-t1 = 90-30 = 60 ms. Pendant la durée T(s) , l'onde se déplace d'une longueur d'onde l (m) à la célérité v (m/s). - La célérité de l'onde dans la corde est : 5,0 m.s-1 ; 10,0 m.s-1 ; 15,0 m.s-1 . v= 0,3 / 0,06 = 5,0 m.s-1 ; - Dans la même expérience, parmi les graphes 3, 4, 5 et 6 ci-dessous, celui représentant l'aspect de la corde à l'instant de date t = 180 ms est le : graphe 3 ; graphe 4 ; graphe 5 ; graphe 6 . 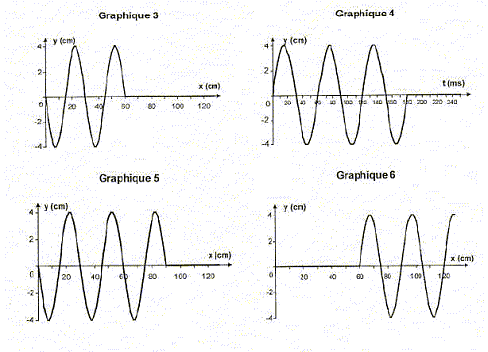 L'aspect de la corde à l'instant de date t = 180 ms est un graphe du type y = f(x) En 0,18 s, à la célérité v = 5 m/s, l'onde parcourt : 5*0,18 = 0,9 m = 90 cm. Donc graphe 5. IV. Ondes lumineuses 1 La propagation de la lumière visible : - Montre que c'est une onde mécanique ; faux, la lumière peut se propager dans le vide, c'est une onde électromagnétique; une onde mécanique a besoin d'un milieu pour se propager. - S'effectue avec une célérité plus petite dans l'eau que dans le vide (indice de réfraction de l'eau : n = 1,3) ; exact : indice de réfraction de l'eau = célérité dans le vide / célérité dans l'eau ; l'indice étant supérieur à 1 alors la célérité dans l'eau est plus faible que dans le vide. - S'effectue avec la même célérité, dans un milieu dispersif donné, quelle que soit la fréquence de la radiation. faux, dans un milieu dispersif , la célérité dépend de la fréquence. 2. La lumière rouge : - Correspond à des longueurs d'onde plus grandes que celles de la lumière bleue ; exact - Se situe dans un domaine de fréquences plus petites que celles du domaine de l'infrarouge ; faux : les longueurs d'ondes de l'infrarouge (IR) sont plus petites que celle de la lumière rouge ; en conséquence la fréquence de la lumière rouge est plus grande que celles des IR - Est moins énergétique que la lumière bleue. exact, plus la fréquence est grande, plus l'énergie transportée est élevée ; la fréquence de la lumière bleue est plus grande que celle de la lumière rouge 3. La lumière visible peut être diffractée. - Le phénomène de diffraction de la lumière visible par une fente est plus marqué pour une fente de largeur 0,5 mm que pour une fente de largeur 5 mm ; exact : La diffraction est d'autant plus marquée que la dimension de la fente se rapproche de la longueur d'onde de la lumière. - Pour une lumière monochromatique, l'écart angulaire du faisceau diffracté par une fente est proportionnel à la largeur de la fente ;faux, voir réponse précédente - L'écart angulaire du faisceau diffracté par une fente de largeur donnée est plus petit pour une radiation rouge que pour une radiation bleue. faux : l'écart angulaire est proportionnel à la longueur d'onde. Or l rouge >lbleu.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
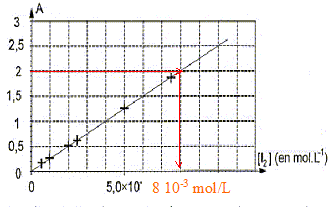
Les parties II et III sont indépendantes. I. Courbe d'étalonnage du spectrophotomètre On dispose de six solutions aqueuses de diiode de concentrations molaires apportées différentes. La mesure de l'absorbance A de chaque solution a été réalisée avec un spectrophotomètre UV-visible réglé à la longueur d'onde l = 500 nm. Le spectrophotomètre utilisé admet une gamme de mesures pour l'absorbance de A0 = 0 à Amax = 2,00. Parmi les espèces chimiques présentes le diiode est la seule espèce qui absorbe à 500 nm. Les résultats obtenus permettent de tracer la courbe d'étalonnage suivante. 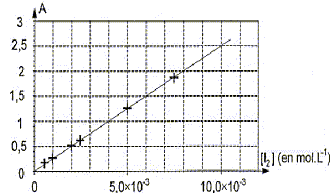
II. Titre du Lugol Pour déterminer le titre en diiode du Lugol, il est ici nécessaire de diluer dix fois la solution commerciale S0. La solution obtenue est notée S0'. Le matériel mis à disposition est le suivant : - bechers 50 mL, 100 mL, 250 mL ;- pipettes jaugées 5,0 mL, 10,0 mL, 20,0 mL ;- éprouvettes graduées 10 mL, 20 mL, 100 mL ;- fioles jaugées 100,0 mL, 250,0 mL, 500,0 mL.
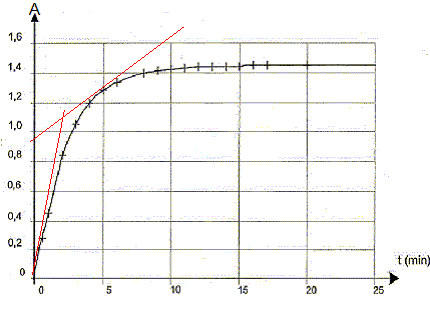
III Étude cinétique d'une transformation chimique mettant en jeu l'eau oxygénée et libérant du diiode La transformation qui a lieu dans l'étude proposée est modélisée par la réaction dont l'équation d'oxydoréduction s'écrit : H2O2(aq) + 2 I -(aq) + 2 H3O+(aq) = I2(aq) + 4 H2O( l) La mesure de l'absorbance du diiode présent dans le milieu réactionnel, à longueur d'onde 500 nm, permet de suivre l'évolution temporelle de la quantité de diiode formé et de réaliser ainsi un suivi cinétique. La courbe A = f(t) est donnée sur la Figure 2. 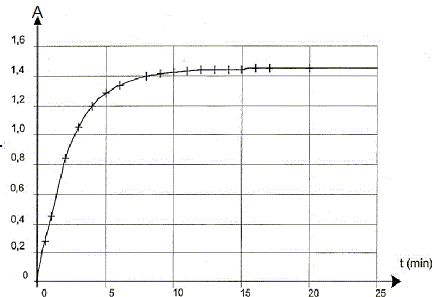 Afin de réaliser ce suivi cinétique :- on prépare une solution S2 (concentration c2) 10 fois moins concentrée que la solution S1 (concentration c1) d'eau oxygénée commerciale ;- on mélange dans un becher, V = 5,0 mL d'acide sulfurique et V3 = 9,0 mL d'une solution aqueuse d'iodure de potassium, K +(aq) + I -(aq) ; - à l'instant de date t0 = 0 s, on introduit rapidement, dans ce becher, un volume V2 = 1,0 mL de la solution S2 d'eau oxygénée H2O2 (aq). Un échantillon du milieu réactionnel est versé dans une cuve que l'on introduit dans le spectrophoto-mètre. Dans les conditions de l'expérience, les ions iodure I - (aq) et les ions oxonium H3O+(aq) sont introduits en excès par rapport à l'eau oxygénée.
corrigé Le graphe est une droite : donc les grandeurs sur les axes sont proportionnelles; elles sont liées par une relation de la forme A = k[I2] avec k = constante. Amax = 2,00 : tracer une horizontale passant par A =2 et déterminer l'abscisse correspondante à partir du graphe.
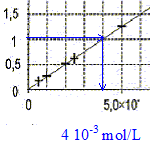
Le facteur de dilution est égal à 10 ; il faut donc que le volume de la fiole jaugée soit 10 fois plus grand que celui de la pipette jaugée. - pipettes jaugées 10,0 mL ;- fioles jaugées 100,0 mL Détermination graphique de la concentration molaire apportée
en diiode de la solution S0'. La concentration molaire apportée cL en diiode du Lugol est dix fois plus grande soit 4,00 10-2 mol/L. L'absorbance de cette solution S0 serait bien supérieure à Amax et le spectrophotomètre ne pourrait pas mesurer son absorbance. oxydant : espèce ion ou molécule suceptible de gagner un ou plusieurs électrons. couple oxydant/réducteur : H2O2(aq)/H2O( l) : H2O2(aq) + 2 H3O+(aq) + 2e- = 4 H2O( l) réduction et I2(aq) /2 I -(aq) : 2 I -(aq) = I2(aq) + 2e- oxydation
[I2](t) = quantité de matière (mol) / volume total (L) = x/Vtot = x/ (V+V2+V3 ) soit x= [I2](t) (V+V2+V3 ) A = k[I2] : dériver A par rapport au temps dA/dt = k d [I2] /dt dériver x par rapport au temps : dx/dt =Vtot d[I2](t)/dt Or v(t) = 1/Vtot dx/dt d'où : v(t) = d[I2](t)/dt = 1/k dA/dt= 1/k dA/dt.
La vitesse de la réaction est proportionnelle au coefficient directeur de la tangente à la courbe ci-dessus à la date considérée. A t=0, la tangente est presque verticale ( coefficient directeur grand) ; à t= 5 min, la tangente se rapproche davantage de l'horizontale ( coefficient directeur plus petit) . Donc v0 > v1. La vitesse diminue au cours du temps car les concentrations ( facteur cinétique ) des réactifs diminuent. L'asymptote horizontale de la courbe ci-dessus indique Afin = 1,45 soit [I2]fin = A/k = 1,45 / 246 = 5,9 10-3 mol/L xfin= [I2]fin Vtot = 5,9 10-3 * 0,015 = 8,84 10-5 mol. xmax = V2 c2 avc c2= c1/10 = 0,089 mol.L -1 et V2 = 10-3 L d'où xmax =8,9 10-5 mol taux d'avancement final t =xfin/
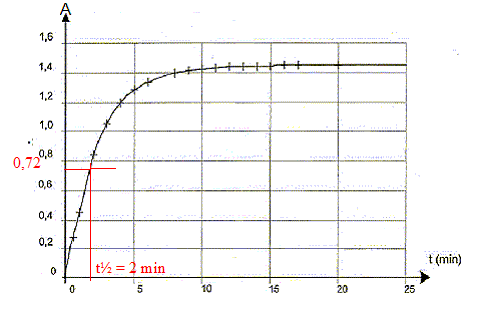
xmax =0,99. temps de demi-réaction t1/2 : durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final. A(t½ )= 0,72 puis lecture graphe
La transformation est totale mais trop lente : elle ne peut pas servir de support à un titrage direct.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La radioactivité se manifeste dans tout l'Univers. On peut utiliser les éléments radioactifs comme des horloges. Selon leur nature et leur durée de vie, ils peuvent renseigner sur l'âge de l'Univers, l'âge de la Terre, les processus géologiques et même l'histoire de l'humanité. On se propose ici de déterminer les dates de tremblements de terre qui se sont produits au cours des siècles à proximité de la faille de San Andreas en Californie. I Radioactivité naturelle du carbone
Données : - numéros atomiques : Z(Be) = 4 , Z(B) = 5 , Z(C) = 6 , Z(N) = 7 , Z(O) = 8 ; - célérité de la lumière dans le vide : c = 2,998 10 8 m.s -1. - masses de quelques particules :
II. Datation par le carbone 14C Deux scientifiques, Anderson et Libby, ont eu l'idée d'utiliser la radioactivité naturelle du carbone 14C pour la datation. Les êtres vivants, végétaux ou animaux, assimilent du carbone. La proportion du nombre de noyaux de 14C par rapport au nombre de noyaux de 12C reste constante pendant toute leur vie. À la mort de l'organisme, tout échange avec le milieu naturel cesse et les atomes de 14C disparaissent peu à peu. La radioactivité décroît alors avec le temps selon une loi exponentielle, qui permet d'atteindre un ordre de grandeur de l'âge de l'échantillon analysé. On admet que le rapport entre le nombre de 14C et 12C est resté constant dans les êtres vivants au cours des derniers millénaires.
corrigé composition en protons et en neutrons des noyaux atomiques suivants 126C et 146C : 126C : 6 protons et 12-6=6 neutrons 146C : 6 protons et 14-6 = 8 neutrons Deux isotopes ne se différencient que par leur nombre de neutrons. 146C--> ZAX + 0-1e consevation de la charge : 6=Z-1 soit Z=7 conservation du nombre de nucléons : 14 = A+0 soit A=14; d'où X est l'élément azote énergie de liaison, en joules, du carbone 14C : El (14C) = Dm c2 = [nombre protons *mp +nombre neutrons*mn - m(14C) ] c2 =(1,672 621 10-27*6 + 1,674 927 10-27*8-2,325 84 10-26) (2,998 10 8 )2= 1,589 10-11 J énergie de liaison par nucléons : El (14C) / A = 1,589 10-11 / 14 =1,135 10-12 J/nucléon énergie libérée par la réaction : Dm réaction c² = [(mélectron + mazote14 - mcarbone14 ] c² =(9,109 381 10-31 + 2,325 27 10-26 -2,325 84 10-26)(2,998 10 8 )2= [- 4,789 06 10-30 ] (2,998 10 8 )2 = - 4,304 10-13 J L'énergie libérée par la réaction est : 4,304 10-13 J
définition du temps de demi-vie t1/2 d'un échantillon radioactif : durée au bout de laquelle la moitié des noyaux initiaux se sont désintégrès expression littérale du temps de demi-vie en fonction de la constante radioactive : à t = t½, n(t½)= 0,5 N0. Repport dans la loi dedécroissance radioactive : 0,5 N0 = N0 exp (-lt½) 0,5 = exp (-lt½) soit : ln0,5 = -lt½ ; ln2 = lt½ soit t1/2 =ln2 / l. l = ln2 / t½ = 0,693 / 5,70 10 3 = 1,22 10-4 an-1. l'activité est le nombre de désintégrations qui se produisent à chaque seconde. Elle s'exprime en becqurel (Bq) A(t) = l N(t) donne l=A(t) / N(t) et A0 = l N0 donne l = A0 / N0 d'où A(t) / N(t) = A0 / N0 ou encore A(t) / A0 = N(t) / N0 . de plus : A(t) =- d N(t) / dt = N0l exp(-lt) et A0 = N0l ; d'où A(t) / A0 =exp(-lt) A3/A0 = 0,223/0,255 = exp(-1,22 10-4 t) s'écrit : ln (0,255/0,233)= 1,22 10-4 t t = ln (0,255/0,233)/ 1,22 10-4=1099 ans soit 1989-1099 = 890 ans après JC. L'activité la plus petite (A2) correspond à l'échantillon le plus ancien : an 586.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||