|
lancer
du poids d'après
bac Nlle Calédonie ( avec calculatrice)- d'après "Labolycée"
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
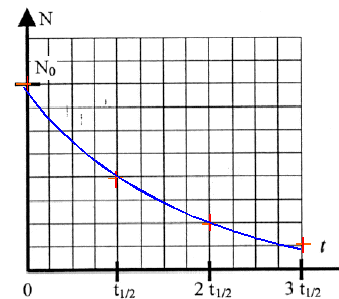
corrigé Le noyau 13153I est composé de 53 protons et 131-53=78 neutrons. Quantité de matière correspondant à 1,00 µg de l'isotope : masse(g) / masse molaire (g/mol) n =10-6 / 131 =7,63 . 10-9 mol Dans une mole d'atomes il y a 6,02 1023 atomes : nombre d'atomes N0 = n NA = 7,63 . 10-9 mol * 6,02 . 1023 = 4,60 1015 atomes Equation de désintégration : 13153I = AZX + 0-1e conservation du nombre de nucléons : 131 =A+ 0 donne A=131 conservation de la charge : 53=Z-1 d'où Z=54 et X est le xénon. La loi de décroissance est donnée par : N(t) = N0 e-lt. La demi-vie représente la durée au bout de laquelle la moitié de la quantité initiale de noyaux radioactifs s'est désintégrée. à t = t1/2, on a N(t) = ½ N0 = N0 e(-lt½). ln ½ = -ln2 = -lt½ soit ln2 = lt½ A chaque fois qu'une durée égale à une demi-vie s'est écoulée, la moitié des noyaux radioactifs initialement présents disparaît
dériver par rapport au temps : N(t) = N0 e-lt. dN(t)/dt = N0(-l)e-lt= -lN(t) ; |dN(t)/dt|=A= lN(t) A t= 0, on a A0 = l N0 ; or l = ln2 / t½ d'où A0 =N0 ln2 / t½ Application numérique : t½=8*24*3600=6,91 105 s ; A0 = 4,6 1015 *ln2/6,91 105= 4,61 109 Bq. A t = 4 heures = 4*3600= 1,44 104 s : A = lN(t) =lN0e-lt avec l =ln2 / t½ = ln2/(8*24*3600)=1,0 10-6 s-1 ; l t = 1,0 10-6 *4*3600=1,44 10-2. A = 4,6 1015 *1,0 10-6 exp(-1,44 10-2)= 4,53 109 Bq. La perte relative
vaut : (4,61-4,53)/4,6=0,017 soit 1,7 %.
Par calcul du temps au bout duquel l'activité de l'iode vaut 4,53 109 Bq. A = A0e-lt avec l =ln2 / t½ = ln2/(13,2*3600)=1,46 10-5 s-1 ; 4,53 109 = 4,61 109 exp(-1,46 10-5t); exp(-1,46 10-5t)=0,98 -1,46 10-5t = ln 0,98= -1,75 10-2 ; t =1,75 10-2 / 1,46 10-5= 1,84 105 =1198 s voisin de 20 min.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
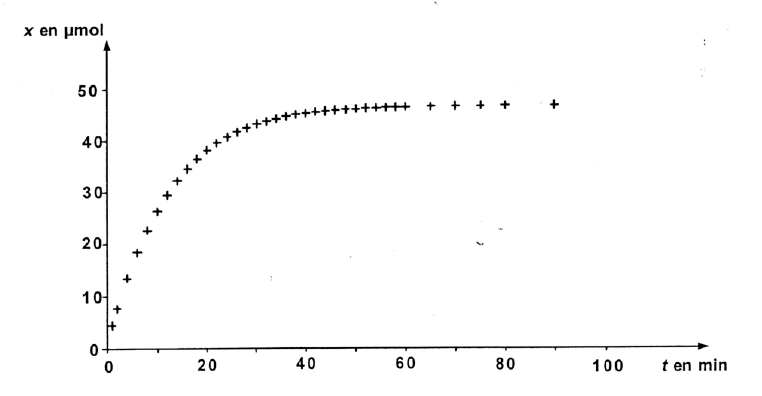
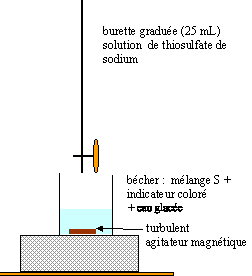
Les ions iodures I- réagissent avec les ions thiosulfate S2O82-. L'équation associée à cette réaction s'écrit : 2I-(aq) + S2O82-(aq) = I2(aq) + 2 SO42-(aq) (1) En présence d'ion iodure, le diiode se transforme en triiodure I3- de couleur brune. Pour simplifier l'écritue, on raisonnera à partir de l'équation (1) sans tenir compte de la formation des ions triiodure. A un instant pris comme origine des dates (t=0), on réalise un mélange réactionnel S à partir d'un volume V1=10,0 mL de solution aqueuse d'iodure de potassium ( K+ ; I-) de concentration molaire en soluté apporté c1= 0,50 mol/L et d'un volume V2 = 10,0 mL d'une solution de peroxodisulfate de sodium (2Na+ ; S2O82-) de concentration molaire en soluté apporté c2=5,0 10-3 mol/L.
corrigé Réaliser un suivi conductimétrique, la solution contenant des ions dont les concentrations varient. A = k c d'où k = A/c =1,7 / 5 10-3 = = 3,4 102 L.mol-1. Quantité de matière en diiode (mol) = concentration (mol/L) * volume de la solution (L) nI2 (t) = c VTotal = c (V1 + V2) = A(t) / k (V1 + V2) A t = 90 min, A (t)= 0,79, d'où nI2 =0,79/340( 10 +10)10-3 = 4,6 10-5 mol. La vitesse volumique v de réaction est proportionnelle à dx/dt, coefficient directeur de la tangente à la courbe au point considéré. Or les tangentes à la courbe sont de plus en plus inclinées sur l'horizontale lorsque le temps augmente. Le coefficient directeur de ces droites tangentes,et en conséquence la vitesse, est maximum à t =0 puis diminue pour atteindre une valeur nulle (partie horizontale de la courbe). La concentration des réactifs, un facteur cinétique, est maximum au départ puis diminue car les réactifs sont consommés : en conséquence la vitesse de réaction diminue au cours du temps. En augmentant la
température (facteur cinétique), on peut obtenir plus rapidement la
même quantité final de diiode.
L'équivalence correspond au changement de réactif limitant. A l'équivalence
les quantités de matière des réactifs sont en quantités
stoechiométriques
nI2 =xéqui nI2 = 0,5* 2,5 10-3* 9,2 10-3 = 1,15 10-5 mol de diiode dans 5 mL Donc dans 20 mL
du mélange réactionnel S : 4*1,15 10-5 = 4,6 10-5 mol.
I2/I- : 2 I- = I2 + 2 e- oxydation S2O82- / SO42- : S2O82- + 2 e- = 2 SO42- réduction
si S2O82-en défaut : 5 10-5 -xmax =0 soit xmax =5 10-5 mol La quantité maximale de diiode formée nI2 = 5 10-5 mol. L'écart relatif vaut : (5-4,6)/5 = 0,080 soit 8,0 %. L'écart est inférieur à 10% : le résultat expérimental est en accord avec le résultat théorique.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
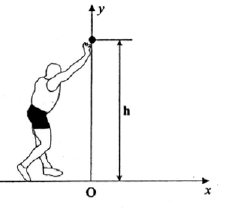
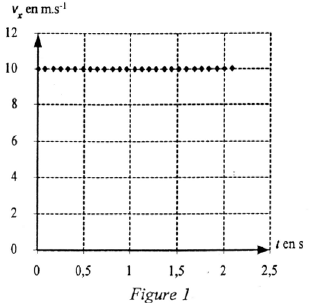
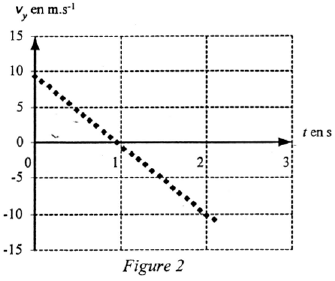
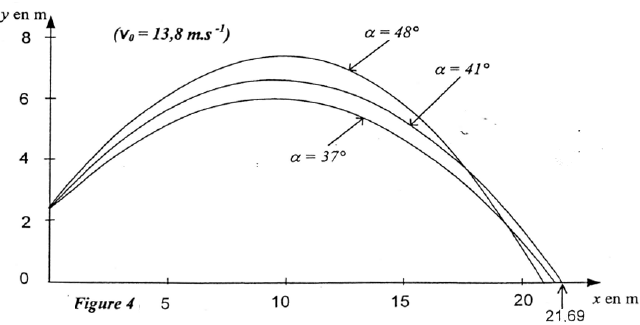
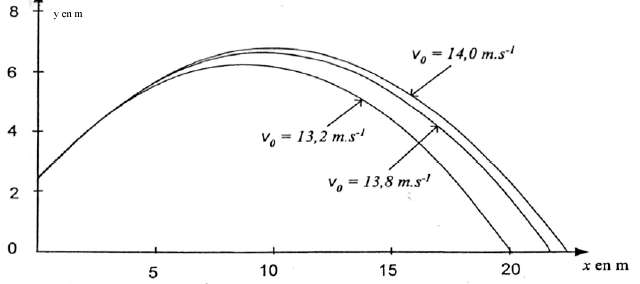
Lors des derniers championnats du monde, le vainqueur du lancer du poids a réussi un jet à une distance D= 21,69 m. Pour simplifier le raisonnement on ne travaillera que sur le centre d'inertie du boulet ( nom courant donné au poids) . l'entraîneur de l'un de ses concurrents souhaite étudier ce lancer. Pour cela il dispose pour le centre d'inertie du boulet, en plus de la valeur 21,69 m du reccord, de la vitesse initiale v0= 13,7 m/s mesurée à l'aide d'un cinémomètre et de l'altitude h=2,62 m. Un mogiciel informatique lui permet de réaliser une simulation de ce lancer et de déterminer la valeur de l'angle du vecteur vitesse initiale avec l'horizontale a=43°. L'entraîneur a étudié le mouvement du centre d'inertie du boulet et a obtenu 3 graphes : le graphe de la trajectoire y=f(x) du boulet, les graphes vx et vy en fonction du temps où vx et vy sont les composantes horizontale et verticale du vecteur vitesse. Pour chacun des graphes, les dates correspondant à deux points successifs sont séparés par le même intervalle de temps.
corrigé Quelle que soit la date, en particulier à t=0, et à la date correspondant au passage au sommet S de la trajectoire, la composante v0x de la vitesse est constante et vaut 10,0 m.s-1. En conséquence, suivant l'axe Ox, le mouvement est uniforme. A t = 0, sur la figure 2 on détermine : v0y = 9,40 m.s-1. La valeur v0 du vecteur vitesse initial est donnée par : v0²= racine carrée (v0y² + v0x²) v0 =(9,4²+10²)½=13,7 m.s-1. De plus tan a =v0y/v0x = 9,4/10 = 0,94 ; soit a = 43° Ces valeurs correspondent à celles données dans le texte. Les caractéristiques du vecteur vitesse au sommet S: sa direction est horizontale, son sens est celui du mouvement et sa valeur vS = 10 m.s-1.
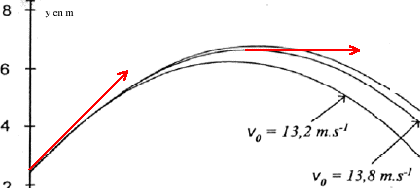
La valeur de la poussée d'Archimède exercée par l'air sur le boulet : PA = m' V g La valeur du poids du boulet : P = m g = m V g Faire le rapport PA/P =m'/m= 1,29/7100=1,8 10-4 soit 0,018 % : la valeur de la poussée d'Archimède est donc négligeable devant le poids du boulet. Bilan des forces : le poids (les autres forces sont négligeables) D'après la 2ème loi Newton, le vecteur accélération est égal au vecteur champ de pesanteur, vertical, dirigé vers le bas, de valeur égale à g. Projection du vecteur accélération sur le système d'axes (O,x,y), on a : (0 ; -g) La vitesse est une primitive de l'accélération : vx(t) = v0x = v0 cos a. vy(t) = - g t+ v0y = -g t + v0 sin a. Le vecteur position est une primitive du vecteur vitesse et à t=0 : x0=0 et y0=h x(t)= v0 cos a t (1) ; y(t) = -½gt² + v0 sin a t + h (2) (1) donne t = x(t)/ v0 cos a repport dans (2) : y = -½gx²/( v0 cos a )² + tan a x + h C'est l'équation de la trajectoire du centre d'inertie du boulet. distance horizontale xmax = D du jet : dériver y par rapport à x et annuler cette dérivée y'= -gxmax/( v0 cos a )² + tan a =0 ; gxmax = ( v0 cos a )² tan a D= xmax = v0² sin a cos a /g = v0² sin (2a ) /(2g ) Quand v0 augmente ( a étant constant) la distance horizontale D du jet augmente. Quand a augmente la distance horizontale D du jet : augmente, passe par un maximum pour a =45° puis diminue. On constate sur la figure 3 qu'une simulation dépasse les 21,69 m. Pour battre le record du monde, il faut avoir (d'après la figure 3) : a = 41° et v0 = 14,0 m.s-1.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|