Aurélie juin 2005

Lunette astronomique

d'après bac Liban 2005 sans calculatrice




Google



 

En 1611, kepler propose le principe de la lunette astronomique, avec des lentilles convergentes pour l'oculaire et l'objectif. Il améliore la lunette de Galilée, mais l'image est renversée. Kepler ne mettra cependant pas son idée en pratique, et il faudra attendre 1617 pour voir apparaître les premières lunettes astronomiques.

On se propose de modéliser une lunette astronomique à l'aide de deux lentilles convergentes :
- une lentille L1 de distance focale f'1=60 cm.

- une lentille L2 de distance focale f'2= 10 cm.

A. Etude de la lentille L2.

  1. Calculer la vergence de la lentille L2.
  2. Compléter les figures ci-dessous en indiquant dans chaque cas les foyers de la lentille L2 et la construction de l'image A2B2 de l'objet A1B1. Echelle horizontale 1/5; échelle verticale 1/1.
  3. Retrouver par le calcul la position de l'image dans le cas de la première figure ci-dessus.

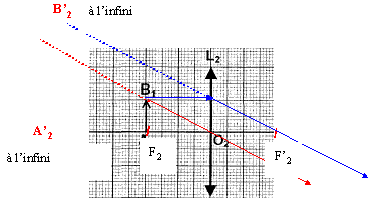
B. Etude d'un modèle de lunette astronomique :

On reprend la lentille L2 à laquelle on associe la lentille L1, pour simuler sur le banc d'optique une lunette astronomique utilisée pour observer un objet AB. On se place dans le cas où l'objet intermédiaire A1B1 est situé dans le plan focal objet de la lentille L2. La distance des centres optiques des deux lentilles est fixée à 70 cm.

  1. Quel rôle joue A1B1 pour la lentille L2 ?
  2. Comment nomme-t-on , dans ce système optique, les lentilles L1 et L2 ?
  3. Compléter la figure ci-dessous en traçant la lentille L1 et son centre optique O1, les foyers des deux lentilles, l'image intermédiaire A1B1 de hauteur 1 cm, le tracé de deux rayons lumineux traversant les deux lentilles du système optique en passant par B1. Echelle horizontale 1/10 , verticale 1/1.
  4. D'après la construction précédente, où se trouve l'objet AB ? Où se trouve l'image définitive A2B2 ?
  5. Une des caractéristique du système optique est son grossissement défini par le rapport du diamètre apparent de l'image à celui de l'objet : G= a'/a.
    - Définir le diamètre apparent     a de l'objet et a ' de l'image.
    - Indiquer ces deux diamètre apparents sur la figure.
    - Exprimer G en fonction des deux distances focales des deux lentilles puis le calculer.
    - En déduire un moyen d'augmenter le grosssissement d'une lunette astronomique.

corrigé


vergence C2 = 1/f'2 = 1/0,1 = 10 dioptries (10 d)

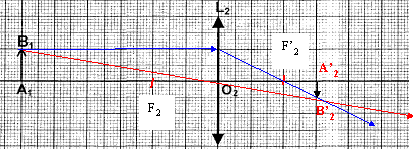
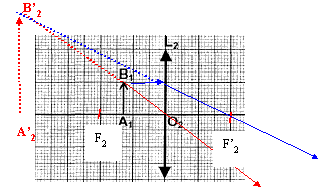
les grandeurs algébriques sont écrites en bleu et en gras.

formule de conjugaison C2 = 1/O2A'2-1/O2A2 avec O2A2= -0,3 m ( 6 carreaux et échelle 1/5)

1/O2A'2= C2 +1/O2A2 = 10 -1/0,3 = 10-10/3 =20/3 soit O2A'2 = 3/20 = 0,15 m ( 3cm en tenant compte de l'échelle)
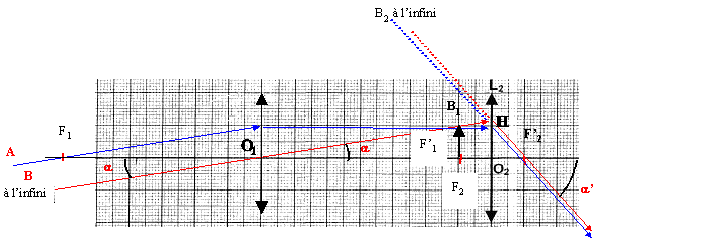
A1B1 joue le rôle d'objet pour la lentille L2.

L2 : oculaire (elle est du coté de l'œil de l'astronome); L1: objectif.(elle est du coté de l'objet)

L'image intermédiaire A1B1 est dans le plan focal image de L1, donc l'objet AB est situé à l'infini à gauche de L1( A étant sur l'axe optique)

L'image définitive A2B2 est rejetée à l'infini, A2 étant sur l'axe optique. En regardant dans L2 on observe cette image sans fatigue ( image à l'infini)

Le diamètre apparent a de l'objet est l'angle ( exprimé en radian) sous lequel on observe l'objet AB à l'œil nu.

Le diamètre apparent de l'image a ' est l'angle ( exprimé en radian) sous lequel on voit l'objet à travers l'oculaire.

triangle rectangle O2,F'2, H ( H projection de B1 sur L2) : tan a ' = O2H/ O2F'2 = A1B1/f'2.

si a ' petit alors tan a ' voisin a ' = A1B1/f'2.

triangle rectangle O1,F2,B1 : tan a = A1B1 / O1F'1 = A1B1/f'1.

si a petit alors tan a voisin a = A1B1/f'1.

G= a '/a =f'1/f'2 = 0,6 / 0,1 = 6.

Pour augmenter le grossissement il faut augmenter la f '1 distance focale de l'objectif et/ou de diminuer f '2 la distance focale de l'oculaire.

à suivre ...
retour - menu
à bientôt ...