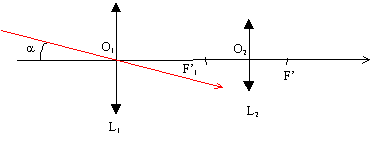
L'importance des observations réalisées par Galilée à l'aide de la lunette conduit Kepler à rédiger, en 1610, le premier traité moderne d'optique, le Dioptricae.

Le point central du Dioptricae est l'étude des phénomènes liés aux lentilles. À l'aide de l'optique géométrique, Kepler explique comment on agrandit ou réduit une image grâce à un choix judicieux de lentilles. Il décrit la lunette galiléenne mais propose un nouveau montage utilisant deux lentilles convergentes.

Une lunette de Kepler, appelée aussi lunette astronomique est constituée de deux lentilles minces convergentes, d'axe optique commun (D). Une modélisation de cette lunette est constituée de la manière suivante :

- L'objectif (L₁) est une lentille convergente de distance focale f₁' = 250 mm, de diamètre D = 25 mm, de centre optique O₁ ;

- L'oculaire (L₂) est une lentille de distance focale f₂' = 50 mm, de centre optique O₂.

1. Schéma de la lunette : faire un schéma en plaçant la lentille (L₂) de telle façon que le foyer objet F₂ de l'oculaire coïncide avec le foyer image F'₁ de l'objectif.
2. Images et grossissement : L'astre observé est à l'infini, son diamètre AB est perpendiculaire à l'axe optique en A. Tous les rayons issus de B sont parallèles entre eux et font avec l'axe optique un angle a qui est le diamètre apparent de l'astre. Un des rayons issu de B est représenté.

   - L'objectif (L₁) donne, de l'astre observé, une image A₁B₁: construire l'image A₁B₁ en justifiant la méthode choisie.
   - Où se forme l'image définitive A₂B₂ donnée par l'oculaire (L₂) ? Justifier la réponse.
   - Compléter la figure en traçant le rayon émergeant de la lunette correspondant au rayon incident tracé issu de B. Justifier les tracés nécessaires à cette construction.

3. On appelle grossissement G d'un instrument d'optique le rapport G=a' /a .a' est l'angle sous lequel on voit l'image donnée par l'instrument. a est l'angle sous lequel on voit l'objet à l'œil nu. Pour les angles petits et exprimés en radians, tana voisin a.
   -Après avoir indiqué a ' sur le schéma montrer que, pour la lunette de Kepler modélisée à la question 1, le grossissement a pour expression G= f'₁ / f'₂ . En déduire la valeur du grossissement de cette lunette.
4. L'expérience montre que les plus belles images du ciel s'obtiennent avec des grossissements dont la valeur est inférieure à un nombre N. Ce nombre est identique à la valeur du diamètre D de l'objectif, exprimé en millimètre, soit ici 25. L'idéal pour l'instrument étudié ici est de disposer d'une gamme d'oculaires permettant des grossissements de N/7 à N. À partir d'un grossissement égal à N les images paraissent floues à l'œil humain.
   - Déterminer pour l'instrument étudié, les deux valeurs extrêmes de f₁' correspondant à ces grossissements.
5. Cercle oculaire
   - Définir le cercle oculaire. Construire le cercle oculaire.
   -Quel est son intérêt pratique ?
6. Nouvelle image et grandissement
   On approche l'oculaire de 5 mm vers l'objectif. Déterminer, par le calcul, la position de l'image définitive A₃B₃.
   - Calculer le grandissement g de l'oculaire dans ce cas.

    

---

---

corrigé

---

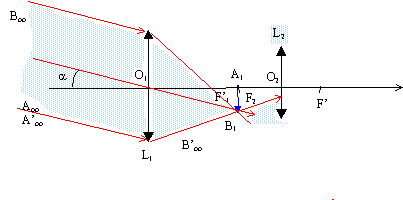
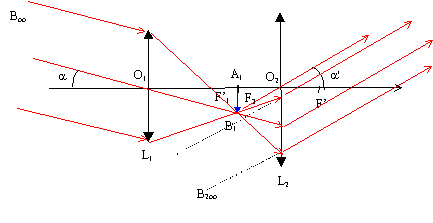
L'objet est à l'infini, son image est donc dans le plan focal image de l'objectif (L₁)

La relation de conjugaison de Descartes permet de le vérifier : (les grandeurs algèbriques sont écrites en bleu et en gras)

1/f'₁ = 1/O₁A₁ - 1/O₁A avec 1/O₁A nul ; donc A₁ est confondu avec F'₁.

Un rayon issu de B et passant par le centre optique O₁de la lentille n'est pas dévié. B₁ est à l'intersection de ce rayon et du plan focal image de L₁.

L'image définitive A₂B₂ donnée par l'oculaire (L₂) est à l'infini car l'objet A₁B₁ est dans le plan focal objet de l'oculaire.

Tracer un rayon passant par B₁ et le centre optique O₂ de la lentille : il n'est pas dévié. Le rayon incident issu de B, ressort de la lentille parallèlement au rayon précédent.

Dans le triangle rectangle F₂O₁B₁ : tan a = A₁B₁ / O₁A₁ = A₁B₁ /f'₁soit a voisin A₁B₁ /f'₁.

Dans le triangle rectangle F₂O₂B₁ : tan a' = A₁B₁ / O₂A₁ = A₁B₁ /f'₂soit a' voisin A₁B₁ /f'₂.

le grossissement a pour expression G=a' / a = f'₁ / f'₂= 250 / 50 = 5,0.

Les deux valeurs extrêmes de f₁' correspondant à ces grossissements : N= 25 mm

G= N =f'₁ / f'₂ soit f'₁ = N f'₂ = 25 *50 =1 250 mm

G= N/7 =f'₁ / f'₂ soit f'₁ = N/7 f'₂ = 25 /7*50 =179 mm

---

Le cercle oculaire est l'image du bord de l'objectif ( lentille circulaire) donnée par l'oculaire.

.

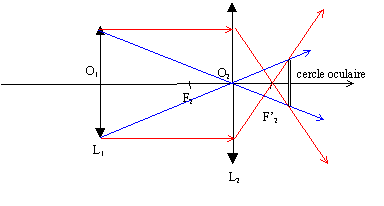
On place l'oeil à la position du cercle oculaire : toute la lumière issue de l'objectif L₁ est collectée par l'oeil ;donc l'image A₂B₂ observée est très lumineuse.

---

A₃B₃ est l'image définitive de A₁B₁ donnée par l'oculaire (L₂). L'oculaire étant plus proche de 5 mm alors O₂A₁= -0,045 m.

On applique les formules de conjugaison à l'oculaire :

1/f'₂ = 1/O₂A₃ - 1/O₂A₁ avec 1//f'₂= 1 / 0,05 = 20 d.

1/O₂A₃ = 1/f'₂ + 1/O₂A₁ =20 - 1/ 0,045 = -2,22 soit O₂A₃ = -1/2,22 = -0,45 m.

grandissement de l'oculaire : g = O₂A₃ / O₂A₁= -0,45 / -0,045 = 10.

---