|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Un ballon sonde, en caoutchouc mince très élastique, est gonflé à l'hélium. Une nacelle attachée au ballon emporte du matériel scientifique afin d'étudier la composition de l'atmosphère. En montant, le ballon grossit car la pression atmosphérique diminue. Sa paroi élastique finit par éclater à une altitude généralement comprise entre 20 et 30 kilomètres. Après l'éclatement, un petit parachute s'ouvre pour ramener la nacelle et son matériel scientifique au sol. Il faut ensuite localiser la nacelle, puis la récupérer pour exploiter l'ensemble des expériences embarquées. Mécanique du vol L'objectif de cette partie est d'étudier la mécanique du vol du ballon sonde à faible altitude (sur les premières centaines de mètres). On peut alors considérer que l'accélération de la pesanteur g, le volume du ballon Vb et la masse volumique r de l'air restent constantes. On modélisera la valeur de la force de frottement de l'air sur le système étudié par l'expression : f = K.rair .v² où K est une constante pour les altitudes considérées et v la vitesse du centre d'inertie du système {ballon + nacelle}. On supposera qu'il n 'y a pas de vent (le mouvement s'effectue dans la direction verticale) et que le volume de la nacelle est négligeable par rapport au volume du ballon. Le système {ballon + nacelle} est étudié dans un référentiel terrestre considéré comme galiléen.
Le poids et la poussée d'Archimède varient-ils avec l'altitude ? Le tableau suivant donne quelques valeurs de grandeurs mesurées au voisinage de la Terre.
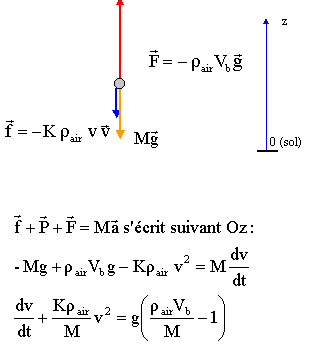
la poussée d'Archimède, verticale, orientée vers le haut, valeur = poids du volume de fluide (air) déplacé : F= rair Vb g avec rair : masse volumique de l'air kg m-3 ; Vb : volume du ballon (m3) le poids du système, verticale, orientée vers le bas, valeur : P= M g la force de frottement de l'air sur le système, verticale, orientée vers le bas, valeur : f = K.rair .v² ( négligeable au début du mouvement car la vitesse est alors très faible) D'après la seconde loi de Newton :
d'où par identification : A = - Krair /M et B = g (rair Vb /M-1). Le ballon s'élève si l'accélération est différente de zéro et orientée vers le haut. Or la vitesse initiale étant négligeable, la force de frottement de l'air est négligeable au moment du décollage. d'où : F - P = M.a ; rair Vb g - M.g = M.a a= (rair Vb / M-1)g positives soit : M<rair Vb. masse maximale de matériel embarqué m" : M = m + m' + m'', m + m' + m'' < rair Vb ; m'' < rair Vb ; - (m + m'). La masse maximale de matériel embarqué: m" = 1,22 *9 -
2,1 - 0,50 = 8,38
kg.
v(tn+1) = v(tn) + D v(tn) avec D v(tn) = a(tn)D t v(t1) = v(t0) + D v(t0) avec D v(t0) = a(t0)D t D v(t0) = 13,6*0,05 = 0,68 m/s d'où v1=0+0,68 = 0,68 m/s or l'équation différentielle donne : a(tn)= Av²(tn) +B = -0,53 v² +13,6 a(t1) = - 0,53*0,682+13,6 = 13,35
m/s²
a(t2) = - 0,53*0,6682+13,35 =
13,11 m/s²
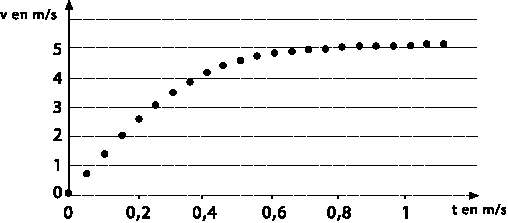
Lorsque la vitesse limite est atteinte, le mouvement devient rectiligne uniforme (l'accélération est nulle dvl/dt = 0) l'équation différentielle s'écrit : 0 = Av²l+B soit vl = (-B/A)½. vl = (-13,6 / (-0,53))½ = 25,66 ½ = 5,06 m/s. D'après le graphe
la vitesse limite vaut environ 5,1 m.s-1. Ce résultat est en
accord avec la vitesse limite calculée.
(g9000-g0) / g0= (9,7789- 9,8066) / 9,8066 = - 0,003 soit - 0,3% donc l'accélération de pesanteur peut être considérée comme constante à moins de 1% près. poussée : F= rair Vb g g est considéré comme constant; rair diminue mais Vb augmente d'après le texte : donc on ne peut rien conclure quant à l'évolution de la valeur de la poussée ( réponse d) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|