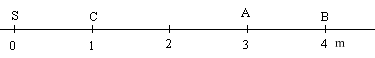|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Une très longue corde élastique inextensible est disposé horizontalement sur le sol. Un opérateur crée une perturbation en imprimant une brève secousse verticale à l'extrémité S de la corde. 
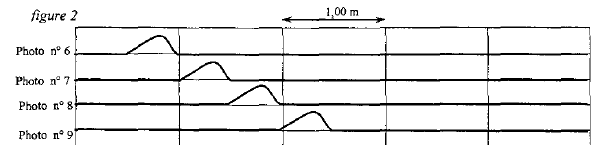
corrigé L'onde se propage le long de la corde placée suivant l'horizontale. La perturbation est verticale, perpendiculaire à la direction de propagation de l'onde : en conséquence, l'onde est transversale. Je calcule la célérité de l'onde ( exprimée en m/s) en divisant la distance AB ( exprimée en m) parcourue par le front de l'onde par la durée correspondante (exprimée en s). Les photos n°6 et n°8 indiquent que le front de l'onde parcourt une distance égale à 1 m en 2*0,25 = 0,5 s. v = 1/0,5 = 2 m/s. Un point de la corde est en mouvement pendant : Chaque point M de la corde reproduit le mouvement de la source S avec un retard q= xM/ v, xM étant la distance SM du point M à la source Or qA= 1,5 s et qB= 2 s ; qA <qB donc A reproduit le premier le mouvement de la source ; le point B présente un retard de 0,5 s par rapport au point Aqui, lui est touché en premier xA= qA v = 1,5*2 = 3 m ; xB= qB v = 2*2 = 4 m ; A est plus proche de la source que le point B. xB-xA= 4-3 = 1 m. Un troisième point C commence son mouvement à l'instant de date tC= 0,50 s. En conséquence ce point est touché par le front de l'onde avant le point A : C est situé à gauche de A tel que xC=qC v = 0,5*2 = 1 m.
La figure 5 indique que : Données : les cordes ont même masse linéique, mais n'ont pas la même tension. le front de l'onde de l'expérience 2a arrive au point K à l'instant ta = 1,50 s . le front de l'onde de l'expérience 2b arrive au point K à l'instant tb = 0,80 s . Le front de l'onde atteint le point K plus rapidement dans l'expérience 2b que dans l'expérience 2a ; donc a célérité de l'onde est plus grande dans l'expérience 2b que dans l'expérience 2a. la tension de la corde modifie donc la célérité de l'onde. De plus, la tension de la corde est plus grande dans l'expérience 2b que dans l'expérience 2a. La célérité de l'onde est d'autant plus grande que la tension de la corde est plus grande. La figure 6 indique que : Données : les cordes sont différentes (masse linéique différente), mais ont la même tension. le front de l'onde de l'expérience 3a arrive au point K à l'instant ta = 1,00 s . le front de l'onde de l'expérience 3b arrive au point K à l'instant de date tb = 1,50 s . Le front de l'onde atteint le point K plus rapidement dans l'expérience 3a que dans l'expérience 3b. La célérité de l'onde est donc plus grande dans l'expérience 3a que dans l'expérience 3b. La masse linéique de la corde modifie donc la célérité de l'onde. De plus, la masse linéique de la corde est plus faible dans l'expérience 3a que dans l'expérience 3b. La célérité de l'onde est d'autant plus petite que la tension de la corde est plus grande.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Toutes les questions de cet exercice sont indépendantes.
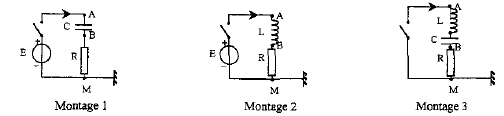
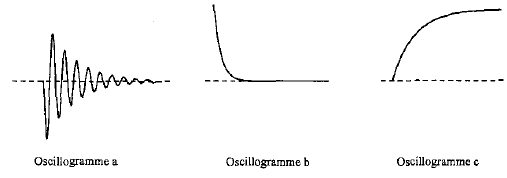
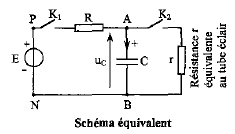
corrigé uR = uBM ; pour visualiser la tension uBM, il faut relié B à l'une des voies de l'oscilloscope et M à la masse. La tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles : visualiser uR s'est donc visualier l'intensité au facteur R près. oscillogramme a : montage 3, circuit RLC Le condensateur initialement chargé se décharge à travers la bobine à la fermeture de K. Il y a échange d'énergie entre condensateur et bobine et vice versa. On observe des oscillations amorties. oscillogramme b : montage 1, circuit RC A la fermeture de l'interrupteur, la tension aux bornes du condensateur croît ( charge). L'intensité du courant décroît de la valeur E/R à zér0 en fin ce charge. oscillogramme c : montage 2, circuit RL On observe un retard à l'établissement du courant du aux
phénomène d'induction ( la bobine stocke de l'énergie) ; puis ensuite
un régime permanent s'établit.
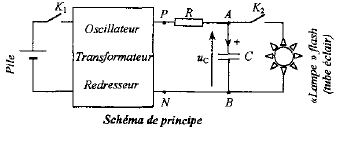
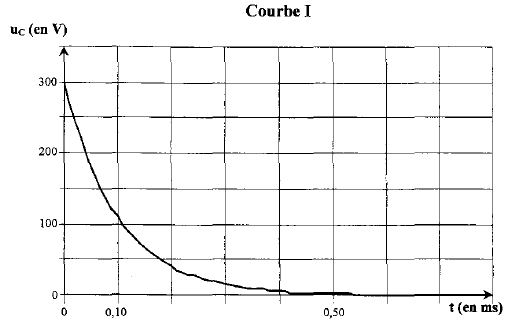
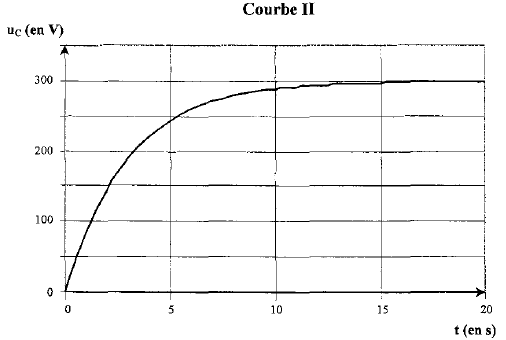
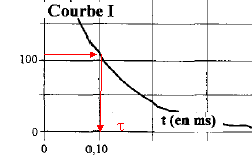
Le condensateur est monté en série avec un résistor et un générateur délivrant une tension continue : le condensateur se charge, la tension à ces bornes uC augmente jusqu'à la valeur 300 V phase 2 : décharge du condensateur, courbe I Le condensateur
est monté en série avec l'ampoule du flash : le condensateur chargé se
décharge, la tension à ces bornes uC diminue jusqu'à la
valeur 0 V.
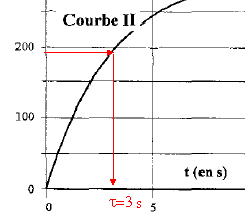
RC= 3 soit R= 3/C= 3/ 10-4 = 3 104 W. décharge : à t= t la tension uC est égale à 37 % de sa valeur finale soit 0,37*300 voisin de : 110 V : le graphe I donne 0,1 ms. rC= 10-4
soit r=10-4/C= 10-4 / 10-4 =1 W.
½CU² = 0,5*10-4*300² = 4,5 J. puissance moyenne mise en jeu lors de chaque phase : phase 1 : 4,5 / (5*3)= 4,5/15 = 0,3 W. phase 2 : 4,5 / (5*10-4)= = 9 103 W. valeur très grande par rapport à la puissance mise en jeu
phase 1, ce qui permet d'obtenir un éclair, un flash très lumineux sur
une durée très courte. L'énergie mise en jeu étant constante phases 1
et 2, la puissance est d'autant plus grande que l'intervalle de temps 5t= 5rC est petit ; c'est à dire plus r est faible.
additivité des tensions E= uR+uC = Ri + uC. i = dq/dt ( avec q >0, charge de l'armature supérieure) or q= CuC soit i = CduC/dt. d'où E= RC duC/dt + uC. phase 2 : les électrons accumulés sur l'armature inférieure du condensateur, se déplacent à travers r vers l'armature supérieure ; le courant circule en sens inverse ( sens conventionnel), dans le sens inverse du sens positif choisi. additivité des tensions 0= ur+uC = ri + uC. i = dq/dt ( avec q, charge de l'armature supérieure) or q= CuC soit i = CduC/dt. d'où 0= rC duC/dt + uC.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Données :
corrigé 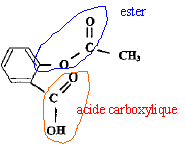
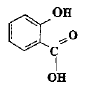
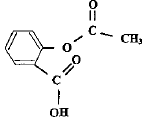
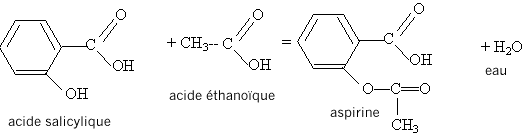
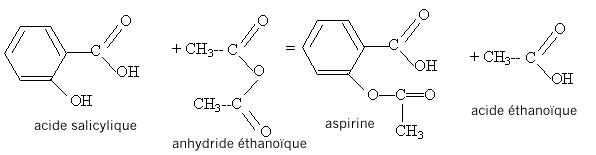
La réaction d'estérification est lente, limitée, athermique : l'avancement maximal ne peut pas être atteint. En ajoutant en excès l'un des réactifs, l'équilibre sera alors déplacé dans le sens direct, formation de l'ester( loi de Le Chatelier) ; l'avancement final va donc croître.
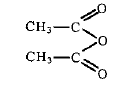
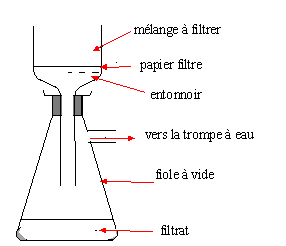
La réaction de l'anhydride éthanoïque avec l'eau est vive et exothermique : il faut donc que le ballon soit parfaitement sec, pour éviter cette réaction. L'acide sulfurique joue le rôle de catalyseur. La température est l'un des facteurs cinétiques : elle augmente la vitesse de la réaction. Le chauffage à reflux permet de travailler à température modérée en évitant les pertes de matière : les vapeurs se condensent dans le réfrigérant à eau et retombent dans le ballon. Pour transformer en acide éthanoïque, l'anhydride éthanoïque utilisée en excès, on ajoute de l'eau. Cette réaction étant vive, il vaut mieux ne pas enlever le réfrigérant.
rendement = quantité de matière d'ester réellement obtenue / Qté de matière d'ester théorique ou encore :
avancement à l'équilibre / avancement maximal
= 0,1 mol = 12,0 / 180 =0,0667 mol xmax=0,1 mol À l'équivalence les quantités de matière des réactifs sont en proportions stœchiométriques ; d'après l'équation chimique ci-dessus : nHA départ = nHO- ajouté nHA départ = cB VBE=5,0 10-1 *10,0 10-3 = 5,0 10-3 mol dans l'échantillon titré, obtenu en prélevant le dixième de la quantité de matière correspondant aux cristaux. soit pour l'ensemble du contenu de la fiole jaugée ( ensemble des cristaux) : 10*5,0 10-3 =5,0 10-2 mol d'aspirine pure dans le solide cristallisé. masse d'aspirine (g) = Qté de matière (mol) * masse molaire aspirine (g/mol) = 5,0 10-2*180 = 1,8*5 = 9 g. Le produit obtenu n'est pas pur.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

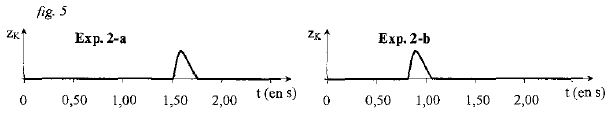
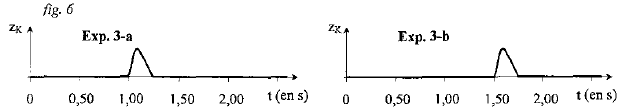
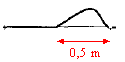 0,5
/ 2 = 0,25 s.
0,5
/ 2 = 0,25 s.