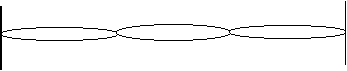|
|
||||
|
|
||||
|
||||
|
|
Expressions théoriques
distance en mètre, célérité (m/s ) et T0 (s) l= v T si T0= nT alors il s'agit d'une onde stationnaire. l= v T et T= T0/ n : l= vT0/ n or T0 = 2L/ v d'où l=2L/n. l = v/ fn= 2L/n
soit fn=v n/(2L).
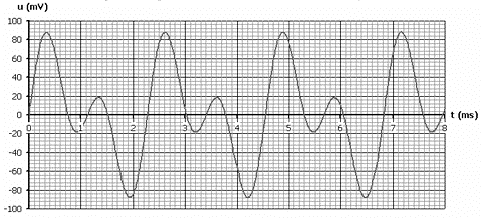
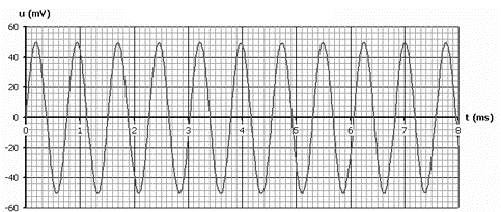
d'une part en vibrant, dans ce cas une corde vibre. d'autre part en émettant un son ( la table d'harmonie joue le rôle de caisse de résonance) 3 périodes correspondent à 6,8 ms = 6,8 10-3 s soit T1 = 6,8 10-3/3 = 2,27 10-3 s. f1 = 1/T1 = 1000 / 2,27 = 441 Hz. vitesse de propagation de l'onde fn=v n/(2L) donne avec n=1 : v= 2Lf1 v= 2*0,68*441= 600 m/s.
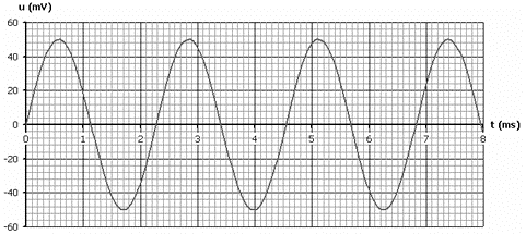
f2 = 1/T2 = 10000 / 7,7 = 1299 Hz. fréquence fondamentale de la corde raccourcie f2 ; longueur L2 ; n = 1 ; v= 600 m/s fn=v n/(2L) donne L= ½ v / f2 =
300/1299 = 0,23
m.
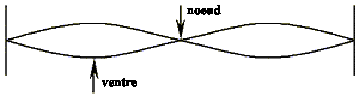
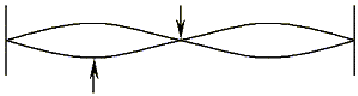
pour le mode de vibration correspondant à l'harmonique de rang 3, la corde présente 3 ventres de vibration
La hauteur d'un son est caractérisée par la fréquence du fondamental. 3 périodes correspondent à 6,8 ms = 6,8 10-3 s soit T'1 = 6,8 10-3/3 = 2,27 10-3 s. f'1 = 1/T'1 = 1000 / 2,27 = 441 Hz. Le timbre d'un son dépend de l'existence des harmoniques. Les deux sons ont même hauteur, les deux instruments jouent la même note. Par contre, ils n'ont pas le même timbre : Le son de fréquence f1 est un pur, sans harmonique. Le son de fréquence f '1 contient des harmoniques (la tension n'est pas un signal sinusoïdal).
|
|||
|
|
 .
.