|
|
|||||
|
|||||
|
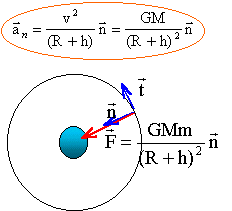
le satellite est soumis à la seule force de gravitation centripète exercée par la planète
M : masse (kg) de la planète ; m : masse du satellite (kg) ; R (m) rayon planète ; h (m) altitude depuis le sol suivant l'axe n la seconde loi de Newton s'écrit : GMm /(R+h)² = m aN= mv²/ (R+h) d'où la valeur de la vitesse (m/s): v² =GM / (R+h). indépendante de la masse du satellite la force de gravitation étant perpendiculaire à la vitesse à chaque instant, ne travaille pas et en conséquence ne modifie pas l'énergie cinétique du satellite. la valeur de la vitesse reste donc constante : mouvement uniforme. Par contre la direction de la vitesse change et l'accélération n'est pas nulle. La période de révolution T du satellite (seconde) est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme. 2 p (R+h) =vT élever au carré, puis remplacer v² par l'expression ci dessus. 4p² (R+h) ² = v² T² = GM/ (R+h) T² ou T² =4p² /(GM)(R+h)3. soit T² /(R+h)3 = 4p² / (GM) rapport constant pour une planète donnée.(3ème loi de Kepler) distance en mètre, période en seconde, masse en kg.
|
|||||
|
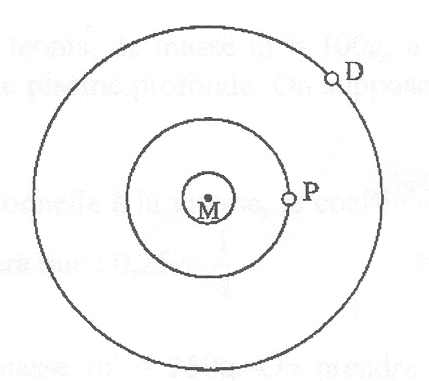
Sous deux aspects au moins Mars est très semblalble àla terre. Tout d'abord elle tourne autour de son axe en 24 h 37 min, ce qui fixe le jour martien à 41 min à peine de plus que le jour terrien. Son axe est incliné de presque 25 ° sur le plan de son orbite (1), soit 1,5° de plus que l'axe de la Terre. Aussi, comme la terre , Mars est soumise à un cycle régulier de saisons. Les deux satellites de mars, Phobos et déeimos, ont été découverts par Asaph Hall. Phobos est un bloc de rocher allongé creusé de cratères. Son diamètre maximum ne dépasse pas 25 km. Il orbite si près de la planète ( 6000 km)(2) qu'il se lève et se couche deux fois par jour martien (3). Deimos est trois fois plus éloigné de Mars et encore plus petit que Phobos, son diamètre n'excédant pas 6 km. (1) 25° est l'angle entre l'axe de mars et la normale au plan de son orbite. (2) 6000 km représente l'altitude du centre de Phobos par rapport au sol martien. (3) Phobos tourne sur son orbite dans le même sens que Mars autour de son axe. G= 6,67 10-11 SI Mars : période de rotation propre autour de l'axe des pôles TM= 24 h 37 min ; rayon de la planète RM= 3400 km ; masse MM. Phobos : période de révolution autour de Mars TP= 7 h 39 min 14 s ; rayon de l'orbite marsocentrique RP.
corrigé Un référentiel galiléen est un référentiel dans lequel les lois de Newton s'appliquent. C'est un référentiel par rapport auquel le Principe de l'inertie est vérifié. Principe de l’inertie : Dans un référentiel Galiléen, si la somme des forces extérieures appliquées à un système est nulle alors le centre d’inertie de ce système est, soit au repos, soit en mouvement rectiligne uniforme.
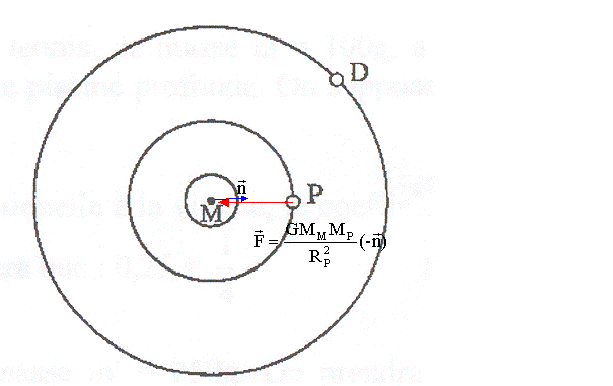
G constante de gravitation universelle (kg-1 m3 s-2); F force (newton) ; MM : maasse de Mars (kg) MP :masse de Phobos (kg) ; RP rayon de l'orbite de Phobos (m). Première loi ou loi des orbites : dans le référentiel héliocentrique, l'orbite de chaque planète est une ellipse dont l'un des foyers est le centre du soleil. Deuxième loi ou loi des aires : le mouvement de chaque planète est tel que le segment de droite reliant le soleil et la planète balaie des aires égales pendant des durées égales. Troisième loi ou loi des périodes : pour toute les planètes, le rapport entre le cube du demi grand axe de la trajectoire et le carré de la période est le même. vitesse de Phobos sur son orbite : Phobos est soumis à la seule force de gravitation F= G MMMP/R²P ; le mouvement est circulaire uniforme, donc l'accélération est centripète. La seconde loi de Newton s'écrit suivant l'axe n de la base de Frenet : F=MPv²/RP G MMMP/R²P = MPv²/RP soit v=[GMM/RP]½. période TP de Phobos sur son orbite : Phobos décrit, à la vitesse v, une circonférence de rayon RP en TP seconde 2pRP= vTP soit 4p2R2P= v2T2P remplacer v² par G MMRP : 4p2R2P= G MM/RP T2P 4p2R3P=G MMT2P soit MM = 4p2R3P/(GT2P). RP= (3400+6000)103 m = 9,4 106 m ; TP= 7*3600+39*60+14= 2,76 104 s. MM= 4*3,14²*(9,4 106)3/(6,67 10-11 * (2,76 104)²)=6,5 1023 kg. Phobos et Deimos ne s'écrasent pas sur Mars en raison de leur vitesse qui n'a pas ou peu changée depuis qu'ils sont en orbite. En effet, ils tournent suffisamment vite pour ne pas "tomber", et comme il n'y a pas de frottement (donc de déperdition d'énergie) dans l'espace, ils conservent leur vitesse. La force gravitationnelle exercée par Mars sur ces deux satellites a pour effet de maintenir ces deux satellites sur une trajectoire circulaire; en absence de cette force il s'éloigneraient de Mars suivant un mouvement rectiligne uniforme ( principe d'inertie) |
|||||
|
|