dipôle RL
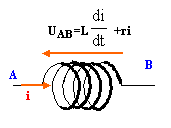
Une bobine inductive est caractérisée par son inductance, notée L, grandeur positive, exprimée en heny (H). Cette bobine possède une résistance électrique, notée r (ohm). fermeture de l'interrupteur d'un circuit inductif : la bobine stocke de l'énergie ( ½Li², avec i : intensité en ampère) et en conséquence entraîne un retard à l'établissement du courant. constante de temps : t = L / S résistances.	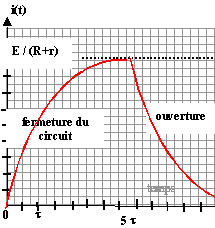On considère le circuit série ci-dessous comprenant un générateur de fem E positive, une bobine d'inductance L et de résistance r, un interrupteur K et un conducteur ohmique de résistance R. A l'instant t= 0 on ferme l'interrupteur.   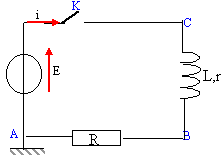Exprimer la tension aux bornes de la bobine ainsi qu'aux bornes du conducteur ohmique en fonction de i(t). Préciser les unités usuelles des grandeurs utilisées. On désire visualiser en voie A d'un oscilloscope les variations de l'intensité en fonction du temps : Quels sont les branchements à réaliser ? Justifier. Etablir en fonction des grandeurs caractéristiques des dipôles, l'expression de l'intensité I du courant lorsque le régime permanent est établi dans le circuit. Tracer l 'allure de la fonction i(t) en précisant littéralement l'ordre de grandeur de la durée du régime transitoire correspondant à l'établissement du courant. Donner l'expression de l'énergie magnétique emmagasinée par la bobine lorsque le régime permanent est établi.   corrigé tensions : tension aux bornes de labobine : uCB = Ldi/dt + ri tension aux bornes du résistor : uBA = Ri r et R en ohms; L en henry ; intensité en ampère et tension en volt. Pour un résisor la tension et intensité sont proportionnelles : donc visualiser la tension aux bornes du résistor, c'est visualiser l'image de l'intensité au facteur R près. Pour visualiser à l'oscilloscope la tension uBA le point A est relié à la masse et le point B est relié à l'une des voies. intensité : en régime permanent ( intensité constante) di/dt =0 d'où E = R I + rI soit I = E / (R+r) la durée du régime transitoire est voisin de 5 fois la constante de tempts t = L / (R+r) pendant cette durée la bobine stocke de l'énergie. 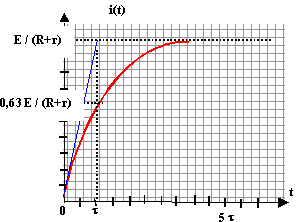énergie magnétique stockée par la bobine : ½L I².
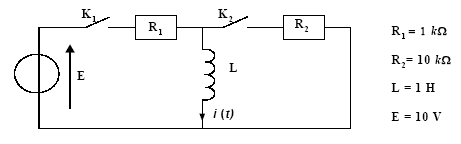
On étudie le montage suivant. Initialement K1 et K2 sont ouverts depuis un temps très long, la bobine est considéré comme idéale (sa résistance interne est nulle). A t = 0, on ferme l’interrupteur K1, l’interrupteur K2 reste ouvert. Ecrire l’équation différentielle vérifiée par le courant i (t) dans la bobine. La solution de cette équation différentielle est de la forme i(t) =A +Bexp(-t/t), donner les expressions littérales de A, B et t. Donner la valeur numérique de t. Donner la valeur numérique de i (t) pour t = 0,5 ms et pour t = 5 ms. A t = T on ouvre K1 et on ferme K2 de façon simultanée. En prenant une nouvelle origine des temps telle que t'= 0 corresponde à t = T, écrire l’équation différentielle vérifiée par i (t') , courant dans la bobine. La solution de cette équation différentielle est de la forme i(t') =A' +B'exp(-t'/t'), donner l’expression littérale de t'. Que vaut A' ? Donner la valeur numérique de t' . Indiquer la valeur numérique de B' dans les deux cas suivants : T= 0,5 ms et pour T = 5 ms. 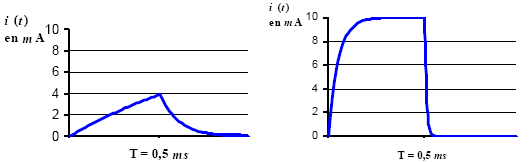Tracer l’allure de i (t) dans les deux cas suivants : T = 0,5 ms et pour T= 5 m   corrigé E= R1i + Ldi /dt solution de cette équation différentielle : i(t) =A +Bexp(-t/t), avec t = L/R1 = 1/1000 = 1 ms = 10-3 s. A valeur du courant en régime permanent : A = E/R1 = 10*/1000 = 0,01 A = 10 mA et B= -A. i(t=0,5 ms)= 0,01(1-exp(-0,5/1))= 3,94 mA. i(t=5 ms)= 0,01(1-exp(-15/1))= 9,93 mA. Ldi/dt + R2i=0 solution de cette équation différentielle : i(t') =A' +B'exp(-t'/t'), avec t' = L/R2 = 1/10000 = 0,1 ms = 10-4 s. B' valeur initiale de l'intensité à t= T, fermeture de K2, ouverture de K1. B'= 3,94 mA si T= 0,5 ms ; B'= 9,93 mA si T= 5 ms.
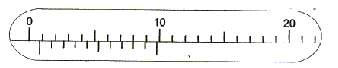
électricité but : déterminer les caractèristiques de quelques bobines Détermination du courant admissible dans la bobine : On mesure la section du fil utilisé pour le bobinage à l'aide d'un pied à coulisse. On donne ci-dessous un agrandissement du vernier. - Quel est le diamètre du fil ? - Quelle est sa section ? - Estimer l'intensité du courant que peut supporter ce bobinage. Détermination des paramètre R et L de la bobine : On étudie la réponse à un échelon de tension d'un circuit R-L. 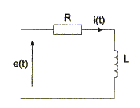e(t) est une tension qui vaut 0 pour t<0 et e(t) = E pout t>=0 - Etablir l'équation différentielle qui lie i(t) à R, L et E. - Résoudre cette équation. - En tenant compte des conditions initiales montrer que : i(t) = E/R(1-exp(-t/t)) avect = L/R - Tracer l'allure de cette courbe. 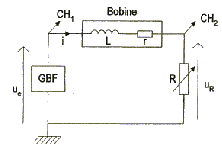Réalisation pratique : Le générateur basse fréquence est utilisé en signal carré variant entre -5 V et 5 V, ces valeurs étant réglées à vide. sa fréquence a été choisie suffisamment petite pour que le régime transitoire soit entierement fini à la fin de chaque demi-période. On visualise ue et uR sur les deux voies d'un oscilloscope. - Pour quelle valeur de R obtient-on : uR(½T) = 0,5 ue(½T) - Comment peut-on utiliser les calibres de l'oscilloscope pour obtenir avec précision le rapport ½ ? - On enregistre sur la voie 2 le signal uR pour deux réglages différents de la base de temps.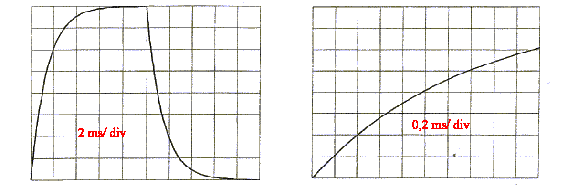 . Quelle est la fréquence du GBF ? . Déterminer la constante de temps . Comment l'impédance interne du GBF influe-t-il sur la mesure de la constante de temps ? . En déduire la valeur de l'inductance L de la bobine sachant que R= 11 W, r= 11 W et que la résistance interne du GBF est 50 W. Etude du domaine de fréquence d'utilisation de cette bobine : On désire étudier l'évolution des paramètres r et L de la bobine en fonction de la fréquence d'utilisation. Pour cela on utilise le montage suivant où le générateur délivre une tension sinusoïdale de fréquance variable.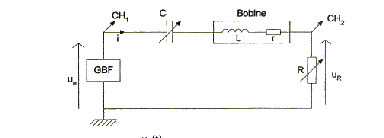 - Montrer que l'on obtient uR(t) = ½ue(t) lorsque LCw²=1 et R = r. - On réalise la manipulation pour différentes fréquences et on obtient les résultats suivants : f(Hz) 100 200 500 1000 2000 5000 10000 R ohm 11 11 14 23 47 207 810 C( nF) 25000 6300 1000 250 64 10 2,5 Justifier la variation de R et donc de r avec la fréquence. - Pour les différentes fréquences calculer la valeur de L. Conclusion. - Calculer et tracer l'évolution du facteur de qualité de la bobine Q=Lw/R en fonction de la fréquence. - Conclure en donnant le domaine de fréquences dans lequel le fonctionnement de la bobine est correct.  corrigé diamètre du fil : 0,8 mm section 3,14 d²/4 = 3,14*0,8²/4 = 0,5 mm² l'intensité que peut supporter ce fil est de l'ordre de l'ampère. Un fil de section 1,5 mm² peut supporter 10 A La résistance électrique est proportionnelle à l'inverse de la section ; l'effet Joule est proportionnel à la résistance électrique. 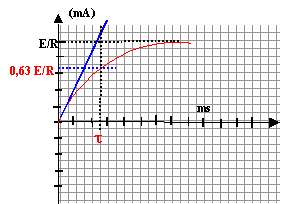e(t) = Ri + Ldi/dt : pour t >=0 E= Ri + Ldi/dt solution particulière de cette équation : i= E/R ( en régime permanent) solution générale de Ri + Ldi/dt =0 : i (t)= A exp (-t/t) avect = L/R solution générale de l'équation différentielle : i (t)= A exp (-t/t) + E/R à t=0 l'intensité est nulle d'où : 0=A+E/R soit A= -E/R i(t) = E/R(1-exp(-t/t)) A la fin de chaque demi période le régime permanent est établit et la bobine se comporte comme une résistance de valeur r ; si r=R on obtient : uR(½T) = ubobine(½T) = 0,5 ue(½T) Comment peut-on utiliser les calibres de l'oscilloscope pour obtenir avec précision le rapport ½ ? par exemple 1 V/div sur la voie 1 et 0,5 V/div sur la voie 2 : les deux courbes sont identiques. fréquence du GBF : une période correspond à 10 div soit 2*10 = 20 ms = 0,02 s ; la fréquence est l'inverse de la période exprimée en seconde : f= 1/0,02 = 50 Hz. 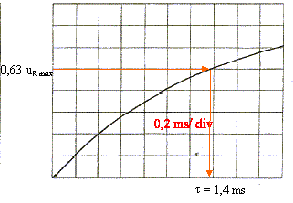constante de temps : à t= t l'intensité est égale à 63% de sa valeur maximale ; donc à t=t, uR= 63% de sa valeur maxi Comment l'impédance interne du GBF influe-t-il sur la mesure de la constante de temps : la constante de temps est égale à l'inductance divisée par la somme des résistance du dipôle RL t = L/SR= 1,4 10-3 s L= 1,4 10-3 (11+11+50)=0,1 H. impédance du dipole RLC : Z=[(R+r)² + (Lw-1/(Cw)²]½ ; à la résonance d'intensité, Lw-1/(Cw)= 0 et l'impédance est minimale, égale à Zmini = R+r. Les effets de la bobine neutralisent ceux du condensateur. uR+uL= (R+r) I0 = ue(t) si R= r alors uR= uL=½ ue(t) En très hautes fréquences (dès 100MHz) l'espacement d'une spire à l'autre présente une capacité parasite qui peut prendre des proportions importantes par rapport à l'effet inductif recherché. Le comportement de la bobine peut se représenter par une bobine idéale en parallèle avec un condensateur idéal pour les effets réactifs. Le schéma est complété par une résistance parallèle Ra qui traduit les pertes du circuit magnétique et par une résistance série Rc qui traduit la résistance du fil électrique enroulé. A fréquence non nulle une partie de la section des conducteurs n'est pas utilisée, les lignes de courant se rejettent mutuellement vers la périphérie, cela augmente la résistance. Lorque la fréquence augmente l'effet de peau modifie la répartition du courant dans le conducteur ohmique, modifiant par la même la résistance de ce conducteur. f(Hz) 100 200 500 1000 2000 5000 10000 w = 2 p f (rad/s) 628 1256 3140 6280 12560 31400 6,28 104 C(F) 2,5 10-5 6,3 10-6 10-6 2,5 10-7 6,4 10-8 10-8 2,5 10-9 w ² 3,94 105 1,58 106 9,86 106 3,94 107 1,58 108 9,86 108 3,94 109 L= 1/(Cw ²) (H) 0,101 0,1 0,101 0,1015 0,1011 0,1014 0,1015 L est constante dans ce domaine de fréquence w (rad/s) 628 1256 3140 6280 12560 31400 62800 Lw 62,8 125,6 314 628 1256 3140 6280 SR = 2R+50 (ohm) 72 72 78 96 144 464 1670 Q= Lw / SR 0,87 1,74 4,02 6,54 8,7 6,8 3,8 Le facteur de qualité passe par un maximum pour une fréquence proche de 2000 Hz. largeur de la bande passante à - 3 dB : Df = S R / (2pL) ; S R voisin de 200 W vers 2000 Hz ; Df voisin 200 / 0,628 voisin 320 Domaine de fréquences : 1840 - 2160 Hz
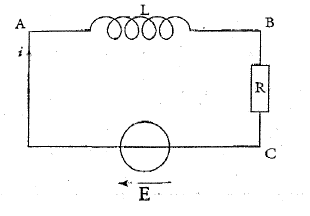
Le circuit ci-dessous est constitué d'un générateur, délivrant un échelon de tension E= 6 V, d'une bobine d'inductance L et d'un conducteur ohmique de résistance R= 120 W. A. Visualisation à l'oscilloscope : Faire apparaître les branchements à effectuer pour visualiser simultanément, sur l'écran de l'oscilloscope, la tension uG aux bornes du générateur, en voie 1 et la tension uR, aux bornes du conducteur ohmique, en voie 2. L'une de ces tensions permet de déduire les variations de l'intensité du courant dans le circuit. Laquelle ? Justifier. Sur l'une des voies on observe la tension U. - Cette tension U correspond-elle à celle visualisée voie 1 ou bien voie 2 ? - Quel phénomène l'observation de la tension U met-elle en évidence ? Quel est l'élément responsable ? Déduire de la courbe représentative de U l'intensité I0 du courant en régime permanent. 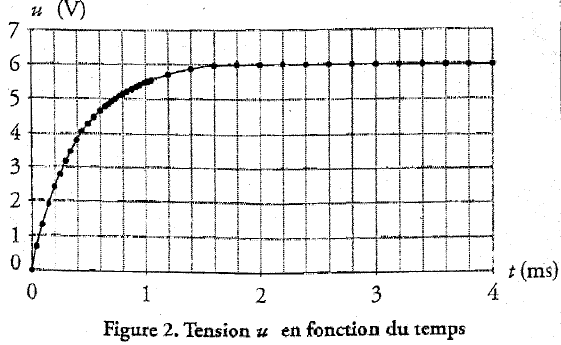B. Constante de temps du dipôle RL : La constante de temps t est donnée par t = L/R; Déterminer à partir de la figure 2, par la méthode la plus appropriée, la constante de temps du dipôle. En déduire la valeur de l'inductance de la bobine. C. Equation différentielle du circuit : L'équation différentielle du circuit, relative à i, étant Ldi/dt + Ri = E, vérifier que cette équation différentielle admet pour solution la fonction i(t) = A(1 - exp(-Bt)) à condition de poser A= E/R et B= R/L. Exprimer la valeur de i(t) quand t= 5t . Conclure. 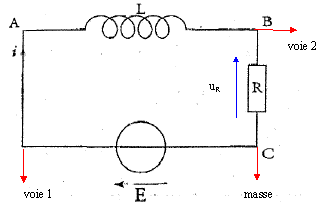corrigé La tension aux bornes d'un résistor est proportionnelle à l'intensité. uR est donc l'image de l'intensité au facteur R près. U correspond à uR, tension visualisée sur la voie 2 : on observe un retard à l'établissement du courant, retard pendant lequel la bobine stocke de l'énergie ; phénomène d'autoinduction dû à la bobine inductive. I0 = 6 / R = 6 / 120 =0,05 A. 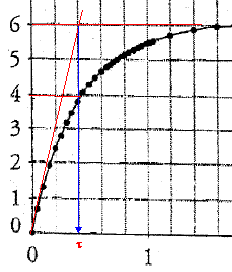t = 0,4 10-3 = L/R soit L= 120*4 10-4 = 4,8 10-2 H = 48 mH. Ldi/dt + Ri = E (1) i(t) = A(1 - exp(-Bt)) ; di / dt = AB exp(-Bt) repport dans (1) : LAB exp(-Bt) + RA(1 - exp(-Bt)) =E LAB exp(-Bt) +RA-RAexp(-Bt) = E A(LB-R)exp(-Bt) +RA=E par identification : RA = E soit A= E/R= 6 / 120 = 0,05A = I0. et LB-R =0 soit B= R/L = 1/t i(5t) = I0(1 - exp(-5))=I0(1 - 6,7 10-3)=0,993 I0. Le régime permanent est pratiquement atteint.
retour -menu