dipôle RC
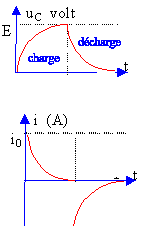
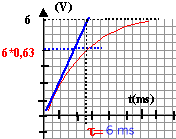
	q = C u   q: charge prise par le condensateur en coulomb (C) u: tension électrique règnant aux bornes du condensateur en volt (V) C: capacité du condensateur en farad (F) énergie en joule (J)   emmagasinée dans un condensateur de capacité C aux bornes duquel règne une tension u E = 1/2 Cu2  charge du condensateur : la tension aux bornes du condensateur croît pour atteindre la valeur de la tension imposée par le générateur de tension constante E. t=RC constante de temps (s) : durée caractéristique de l'évolution du système.   décharge du condensateur, la tension U décroît de E à 0	On considère le circuit suivant comprenant, montés en série : un générateur de tension continue de fem E=6 V et de résistance interne nulle, une résistance R=5 kW, un condensateur de capacité C=1,2mF et un interrupteur K. 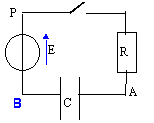Etude de la charge : Préciser sur le schéma du montage, le sens positif choisi pour l'intensité du courant i. Etablir l'équation différentielle de charge liant la tension instantanée uAB(t) aux bornes du condensateur et sa dérivée par rapport au temps duAB/dt en fonction de R, C et E. Vérifier que l'expression uAB(t) = E(1-e-t/(RC)) est solution de l'équation différentielle trouvée précédemment. La tension initiale du condensateur uAB(t=0)=0 est-elle compatible avec les données de l'exercice ? Quelle est la valeur maximale que peut atteindre la tension uAB(t) ? Donner la dimension du produit RC. Comment appelle-t-on ce produit ? Quelle est sa signification pratique pour ce circuit ? 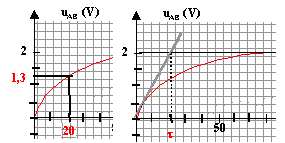Calculer la valeur de la tension instantanée aux instants t=5 ms, t=10 ms, t=20 ms et t=50 ms. Tracer l'allure de la tension uAB(t) Déterminer l'expression de l'intensité du courant i(t) en fonction du temps t et des paramètres E, R et C. Calculer sa valeur numérique à l'instant t=0.. Lorsque t est très grand, que vaut l'intensité du courant ? Bilan énergétique : Quelle est l'expression, en fonction de E et C de l'énergie électrique WC emmagasinée dans le condensateur lorsque la charge est terminée ? La puissance électrique instantanée délivrée par le générateur est p(t) = dWel /dt = Ei(t). Déterminer l'énergie électrique totale Wel délivrée au circuit par le générateur au cours de la charge en fonction de E et C. Déduire des deux questions précédentes l'expression WR, de l'énergie dissipée dans la résistance R au cours de la charge. 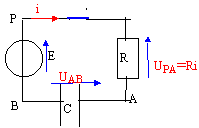corrigé uPB= E ; uPB= uPA+ uAB avec i = dqA/dt = CduAB/dt . E= Ri +uAB soit E=RC duAB/dt +uAB (1) dériver l'expression de uAB par rapport au temps : duAB/dt = E/(RC) e-t/(RC). repport dans (1) : E= RC*E/(RC) e-t/(RC)+E(1- e-t/(RC)) E = Ee-t/(RC) + E-E e-t/(RC) égalité vérifiée. uAB (t=0)= E(1-e0) = E(1-1)=0 condensateur initialement non chargé. uAB (t=oo)= E(1-0) =E condensateur entièrement chargé. t =RC = 5 103*1,2 10-6 = 5 10-3s = 5 ms constante de temps en seconde. Au bout de 5t le condensateur est considéré comme chargé. t = 5ms t=10 ms t= 20 ms t= 50 ms uAB =6(1-0,37) =3,78 V uAB= 4,87 V uAB= 5,78 V uAB= 6 V i = CduAB/dt = C E/(RC) e-t/(RC)= E/R e-t/(RC). à t=0 l'intensité vaut : 6/5000 e0 = 6/5000 = 1,2 mA. au bout d'un temps infini l'intensité est nulle. 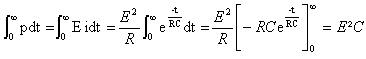énergie stockée par le condensateur chargé : WC= ½CE² énergie fournie par le générateur : Wel = WC+WR d'où WR= ½CE²
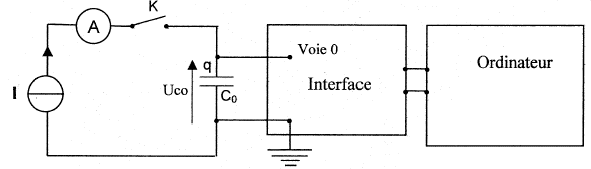
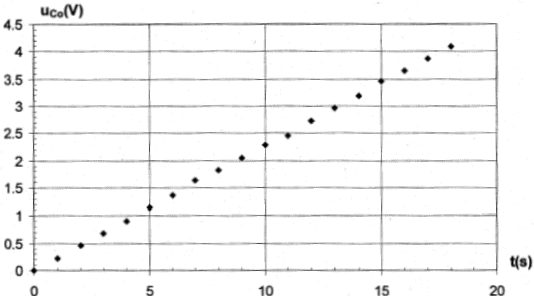
	condensateur et dipôle RC Pour déterminer la capacité d'un condensateur on réalise la charge à l'aide d'un générateur de courant. Ce générateur débite un courant d'intensité constante I= 0,50 mA. La saisie automatique de la tension uc aux bornes du condensateur en fonction du temps est réalisée avec le montage ci-dessous. On obtient la courbe suivante : A l'instant t=0, le condensateur est déchargé et on ferme l'interrupteur K. Etablir l'expression de uc(t) en fonction de I, C0 et t. A l'aide de la courbe déterminer la capacité du condensateur en expliquant la démarche. Etude de la charge d'un autre condensateur à travers une résistance R : on utilise un générateur de tension idéeal de fem E. 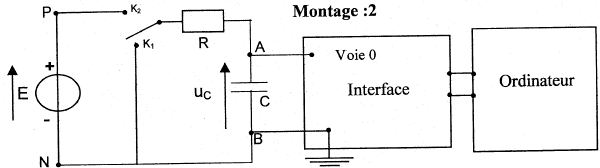A l'instant initial le condensateur est déchargé et l'interrupteur est basculé en position K2. 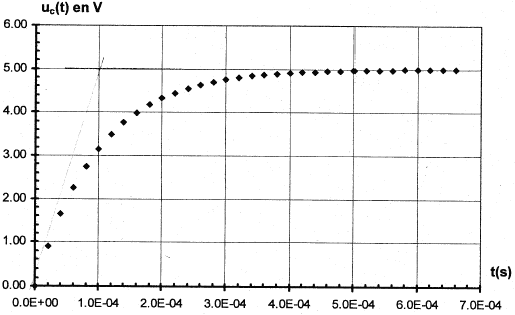On enregistre la représentation suivante de uc(t) Montrer que le produit RC est homogène à un temps. Déduire de la courbe la constante de temps t du dipôle puis calculer la valeur de la résistance R si C= 1 m F. Indiquer la méthode suivie. 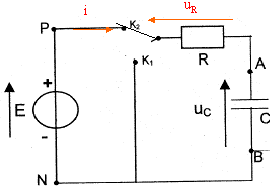Recopier le schéma du circuit ( sans l'interface ni l'ordinateur) puis préciser l'orientation positive choisie pour le courant i et y ajouter la flèche représentative de la tension uc. Etablir la relation entre uc, uR et E. Etablir l'équation différentielle à laquelle satisfait uc. Déterminer la valeur de E en justifiant. Déterminer la valeur de l'intensité i à t= 0 ; justifier. Déterminer la valeur de l'intensité i pour t >5t. Justifier. Montrer que duc/dt = 104(5-uc) relation 1. Résolution numérique de l'équation différentielle par la méthode d'Euler : la méthode de résolution numérique permet de trouver des couples de valeur (t ; uc) qui vérifient l'équation différentielle de la relation 1. On rappelle que les couples de valeurs sont liés par la relation uc(ti+1) = uc(ti) + [duc/dt)ti D t avec Dt = 5 10-5 s. Compléter le tableau suivant : ti(s) [duc/dt)ti uc(ti) (V) 0 5 10-5 10-4 1,5 10-4 tableau donné à titre d'exemple, tableau réel remis avec la copie.   corrigé q= It ; charge en coulomb, intensité en ampère et temps en seconde uc=q/C0= I/C0t droite de coefficient directeur I/C0. le coefficient directeur est déterminé graphiquement : 3,5/15 = 0,233 V/s I/C0=0,233 soit C0 = I/0,233 = 5 10-4 / 0,233 = 2,14 10-3 F= 2,14 mF. R : tension / intensité soit V A-1. C= q/u charge / tension soit intensité* temps / tension ou A s V-1. RC : V A-1 A s V-1 soit s. t = RC= 10-4 s si C= 10-6 F alors R= 100W. 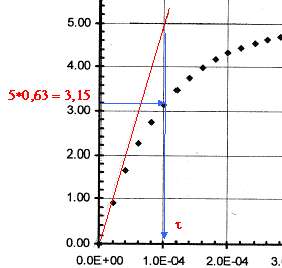constante de temps : intersection de la tangente à l'origine avec l'asymptote horizontale ou bien à t =t , uc= 63% de sa valeur maximale. uc+uR= E avec uR= Ri et i = dqA/dt. or Cuc=qA soit i = dqA/dt = C duc/dt = Cuc'. uc+ Ri = E ; uc+ RCuc' = E. au bout d'une durée supérieure à 5t, le condensateur est chargé ; l'intensité est alors nulle, uR=0 et uc= E= 5 V. à t=0+, le condensateur n'a pas eu le temps de se charger et uc=0. uR=Ri0= E ; i0=E/R= 5 /100 = 0,05 A. uc+ RCuc' = E s'écrit : uc' = 1/(RC) (E-uc) = 1/10-4 ( 5-uc)= 104( 5-uc) ti(s) [duc/dt)ti uc(ti) (V) 0 5 104 0 t1= 5 10-5 2,5 104 2,5 t2= 10-4 1,25 104 3,75 t3= 1,5 10-4 0,625 104 4,37 uc(ti+1) = uc(ti) + [duc/dt)ti D t et duc/dt) = 104( 5-uc) à t=0 , uc(0)=0 ; [duc/dt)]0=104(5-0)= 5 104 V/s ; à t=5 10-5 s , uc(t1)=uc(0)+ [duc/dt)]0 D t =5 104*5 10-5 = 2,5 V [duc/dt)]t1=104(5-2,5)= 2,5 104 V/s ; à t= 10-4 s , uc(t2)=uc(t1)+ [duc/dt)]t1 D t =2,5+2,5 104*5 10-5 =3,75 V [duc/dt)]t2=104(5-3,75)= 1,25 104 V/s ; à t= 1,5 10-4 s , uc(t3)=uc(t2)+ [duc/dt)]t2 D t =3,75+1,25 104*5 10-5 =4,37 V [duc/dt)]t3=104(5-4,37)= 0,625 104 V/s ;
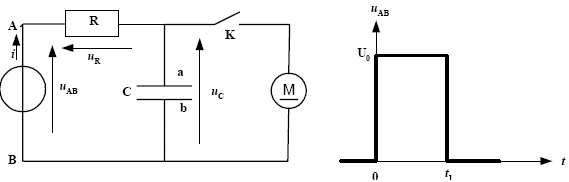
	On utilise le montage ci-dessous comportant une résistance R, un condensateur déchargé C et un moteur M. Cemoteur peut entraîner une poulie permettant de soulever, à l’aide d’un fil, une masse m sur une hauteur h. L’interrupteur K étant ouvert, on applique entre les bornes A et B la tension uAB dont l’évolution en créneau de durée t1, est représentée en fonction du temps. Données : R = 1 k.W ; C = 1000 µF et U0 = 12 V. En supposant que t1--> infini , choisir parmi les cinq courbes ci-dessous, celle qui représente l’évolution en fonction du temps t : -De la tension uc aux bornes du condensateur dont on donnera la valeur numérique maximale atteinte UCM ; - De la tension uR aux bornes de la résistance dont on donnera la valeur numérique maximale atteinte URM ; - Du courant i dans le circuit dont on donnera la valeur numérique maximale atteinte IM . Donner l’expression littérale et la valeur numérique de la constante de temps t de ce circuit. Choisir parmi les réponses proposées, la plus faible valeur de durée t1 du créneau permettant à la tension uc d’atteindre 99% de la valeur UCM. 0,03 s ; 0,12 s ; 1,93 s ; 3,37 s ; 4,61 s ; 5 s ; 9,47 s. On applique maintenant le créneau de tension uAB durant t1 = 100 s. On ferme alors l’interrupteur K. Le moteur soulève la charge m = 10 g sur une hauteur h = 0,35 m et s’arrête. La tension du condensateur dans ces conditions a pour valeur UCA = 4, 8 V. On donne g = 10 m.s-2. Déterminer, au moment de la fermeture de l’interrupteur K, la valeur : - qa de la charge atteinte par l’armature a du condensateur ; - qb de la charge atteinte par l’armature b du condensateur ; - ECE de l’énergie emmagasinée par le condensateur. Calculer, en fin d'ascension de la charge, l’énergie ECA restant emmagasinée dans le condensateur, l’énergie ECF fournie par le condensateur au moteur et l’énergie EM communiquée par le moteur à la charge. - Comparer ECF et EM et conclure.   corrigé courbe III : pendant la charge, la tension uc aux bornes du condensateur croît jusqu'à la valeur U0= 12 V courbe V : pendant la charge, la tension uR aux bornes de la résistance décroît( comme l'intensité )de la valeur U0=12 V jusqu'à la valeur nulle. courbe V : pendant la charge, l'intensité du courant i dans le circuit décroît de la valeur U0/R = 12 / 1000 = 12 mA à zéro. la constante de temps t de ce circuit : t = RC = 1000 * 10-3 = 1 s. la plus faible valeur de durée t1 du créneau permettant à la tension uc d’atteindre 99% de la valeur UCM est égale à : uc= U0(1-exp(-t/t)) ; 0,99 U0 =U0(1-exp(- t1/t)) ; 0,99 =1-exp(- t1/t) ;exp(- t1/t) = 0,01 - t1/t = ln 0,01 = -4,61 soit t1 = 4,61 t = 4,61 s. t1 = 100 s le condensateur est chargé ; la tension à ses bornes vaut 12 V ; C= 10-3 F qa= CU0 = 12 10-3 C ; qb= -qa = - 12 10-3 C ; énergie stockée dans le condensateur : ECE =½q²a/C= 0,5*(12 10-3)2/10-3 = 72 10-3 J. ECA restant emmagasinée dans le condensateur : ½CU²= 0,5*10-3*4,8²= 11,5 10-3 J l’énergie ECF fournie par le condensateur au moteur :(72-11,5)10-3 = 60,5 10-3 J. l’énergie EM communiquée par le moteur à la charge : mgh = 0,01*10*0,35 = 35 10-3 J. rendement du dispositif : EM / ECF = 35/60,5 = 0,58 ( 58 %) les pertes sont très importantes pour un moteur électrique.
	retour -menu