Aurélie sept 04

réfraction, réflexion, lentille, fibre optique

seconde, première S




Google



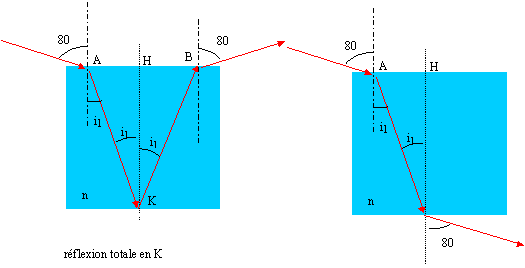
 On veut calculer la vitesse de la lumière dans le verre d'indice n. Pour cela on dispose d'un bloc cubique de verre de 10 cm d'épaisseur. On envoie la lumière d'un laser sur ce bloc avec un angle de 80°. Le faisceau laser ressort du cube de verre à 8,7 cm de la verticale du point d'entrée.

  1. A partir d'une construction précise mesurer au rapporteur l'angle de réfraction aprés la traversée de la surface de séparation entre l'air et le verre.
    - En déduire l'indice de réfraction du verre.
    - Calculer la valeur de la vitesse de la lumiére dans ce bloc de verre. 
corrigé
réfraction sur la face d'entrée :

on passe de l'air (indice n air=1) dans le verre ( indice supérieur à 1) : il y a toujours un rayon réfracté.

soit i1 l'angle de réfraction : sin 80 = n sin i1 avec sin 80 = 0,985.

sur la face inférieure, on passe du verre à l'air ( milieu moins réfringeant d'indice plus petit que le verre) : il n'y a pas toujours de rayon réfracté dans l'air, par contre il y a toujours un rayon réfléchi dans le verre.

dans l'hypothèse d'une réflexion totale sur la face inférieure :

tan i1 = AH/HK=4,35/10=0,435 ; i1 = 25,8°

n sin i1 = 0,985 soit n= 0,985 / sin 25,8 = 0,985 / 0,435 = 2,26

Dans le cas où il y a réfraction en K :

tan i1 = AH/HK=8,7/10=0,87 ; i1 = 41°

n sin i1 = 0,985 soit n= 0,985 / sin 41 = 0,985 / 0,656 = 1,5 ( résultat plus probable pour un verre)

l'indice de réfraction d'un corps était le rapport de la vitesse de la lumière dans le vide à la vitesse de la lumière dans ce corps

donc ici la vitesse de la lumière dans le verre considéré est 3 108/1,5=2 108 m/s.

L'objectif d'un projecteur de diapositives est assimilé à une lentille convergente de distance focale 16,6cm. La distance entre la diapositive et l'écran est de 3 m.

  1. Calculer la position de la diapositive par rapport à la lentille pour avoir une image nette sur l'écran.
  2. Quelles sont les dimensions sur l'écran d'une diapositive de 24 mm sur 36mm.
  3. On approche l'écran de 1 m.
    - Dans quel sens doit-on déplacer la diapositive pour avoir de nouveau une image nette sur l'écran.
    - Quelles sont les nouvelles dimensions de l'image ?     

 

corrigé
Appliquer la relation de conjugaison des lentilles minces convergentes :

les grandeurs algèbriques sont écrites en bleu et en gras

1/OA'-1/OA=1/OF' (1)

avec OF' = 0,166 soit 1/OF' = 1/0,166 =6 ;

distance diapositive lentille + distance lentille écran = 3 m

AO + OA' = 3 ; -OA + OA' = 3 donne OA' = 3 + OA puis repport dans (1)

1/(3 + OA)-1/OA=6

réduire au même dénominateur et faire les produits en croix :

OA-( 3 + OA) = 6 OA( 3 + OA) puis effectuer :

-3 = 6 OA( 3 + OA) ; -1 = 2 OA( 3 + OA) ; -1 = 6OA + 2OA2.

résoudre l'équation du second degré : OA2 + 3OA +0,5 =0

D= 9-4*0,5=7 ; racine carrée (7) =2,646

solution n°1 : (-3 + 2,646 ) /2 = -0,177 m.

solution n°2 : (-3 - 2,646 ) /2 = 2,823 m.

or A est situé à gauche de la lentille ; donc OA est négatif est vaut -0,177 m.

dimensions de la diapositive sur l'écran :

grandissement de la lentille g = OA' / OA = 2,823 / (-0,177) proche de -16

24 mm = 0,024 m ; 0,024*16 = 0,384 m

32 mm = 0,032 m ; 0,032*16 = 0,512 m.

On approche l'écran de 1 m.

distance diapositive lentille + distance lentille écran = 2 m

AO + OA' = 2 ; -OA + OA' = 2 donne OA' = 2 + OA puis repport dans (1)

1/(2 + OA)-1/OA=6

réduire au même dénominateur et faire les produits en croix :

OA-( 2 + OA) = 6 OA( 2 + OA) puis effectuer :

-2 = 6 OA( 2 + OA) ; -1 = 3 OA( 2 + OA) ; -1 = 6OA + 3OA2.

résoudre l'équation du second degré : OA2 + 2OA + 0,333 =0

D= 4-4*0,333=2,67 ; racine carrée (2,67) =1,63

solution n°1 : (-2 + 1,63 ) /2 = -0,185 m.

solution n°2 : (-2 - 1,63 ) /2 = 1,815 m.

or A est situé à gauche de la lentille ; donc OA est négatif est vaut -0,185 m. On éloigne la diapositive de la lentille pour obtenir une image nette.

dimensions de la diapositive sur l'écran :

grandissement de la lentille g = OA' / OA = 1,815 / (-0,185) proche de -9,8

24 mm = 0,024 m ; 0,024*9,8 = 0,235 m

32 mm = 0,032 m ; 0,032*9,8 = 0,314 m.

 TP OPTIQUE
  1. Propagation de la lumière
    - La lumière ce propage-t-elle en ligne droite ?
  2. Expérience 1 :
    - Remplir une cuve d'eau et ajouter quelques gouttes de lait.
    - Diriger un faisceau laser parallèlement au fond de la cuve. Pourquoi introduire du lait dans l'eau ? Comment se propage le faisceau laser dans la solution ?
  3. Expérience 2 :
    - Introduire du chlorure du sodium cristallisé dans l'eau afin de former au fond de la cuve une couche uniforme. Comment se propage le faisceau laser dans cette solution ? Interpréter ce phénomène.
  4. Les miroirs : Comment la lumière est-elle réfléchie par un miroir plan ?
    - Expérience :
    Poser sur une table horizontale un rapporteur et y déposer verticalement un miroir plan (la base du miroir est alignée avec la droite O-O du rapporteur). Diriger un faisceau étroit (une seule fente) de lumière vers le miroir. Le faisceau doit être parallèle à la table et assez proche de celle-ci pour l'éclairer (lumière rasante). Noter vos observations.
    - Exploitation : Rappeler la signification de l'angle d'incidence i.
    Comment peut-on définir l'angle de réflexion ?
  5. Forme et position de l'image donnée par un miroir plan : comparer image et objet
    - Expérience : construire la molécule de méthane en donnant à chaque atome d'hydrogène une couleur.
    Observer l'image donnée par un miroir plan de cette molécule et réaliser le modèle moléculaire identique de l'image
    - Exploitation : la structure de l'objet est-elle identique à celle de l'image ?
    - Situer l'image :
    Expérience : Placer une bougie allumée devant une vitre verticale. Observer l'image obtenue et placer derrière la vitre une bougie identique à la précédente mais éteinte. Mettre la mèche de cette seconde bougie sous l'image de la flamme de première.
    - Exploitation : Quelle position particulière occupe les deux bougies par rapport au plan de la vitre quand la seconde bougie paraît allumée ?

 

corrigé
On a vu en seconde que la lumière se propage en ligne droite dans l'air ou dans un milieu homogène. Par contre si la lumière rencontre un obstacle ou une fente dont les dimensions sont de l'ordre de grandeur de la longueur d'onde de la lumière, on observe le phénomène de diffraction ( dispersion de la lumière dans plusieurs directions au delà de l'obstacle)

On ajoute un peu de lait dans l'eau pour voir le trajet du faisceau laser. Il se propage de manière rectiligne, le milieu étant homogène sans phénomène de diffraction.

Il a un léger mouvement curviligne car la solution est très salée au fond et moins salée en surface ( milieu hétérogène)

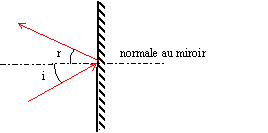
l'angle d'incidence i et l'angle de réflexion r ont la même mesure.

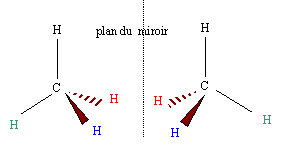
L'objet et l'image ne sont pas superposables; ils sont symétriques par rapport au plan du miroir.

Les deux bougies sont symétriques par rapport au plan de la vitre

Une fibre optique à saut d’indice est constituée d’une âme cylindrique, de rayon R= a, d’axe Ix d’indice constant n1 (cœur de la fibre) entourée d’une gaine cylindrique, de rayon R=b et d’indice n2 inférieur tel que 1<n2<n1. Un rayon lumineux S (monochromatique de longueur d’onde l) arrive sous un incidence q et atteint le cœur de la fibre (face d’entrée) en I selon l’axe méridien de la fibre. n1= 1.520 ; n2= 1.480 ; a = 30 micromètres.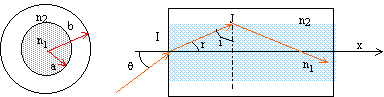

  1. Tracer qualitativement n(R), pour R appartient ]0, + infini[
  2. Exprimer le sinus de l’angle de réfraction r au point d’entrée I en fonction de n1 et q.
  3. L’angle d’incidence sur la surface de séparation cœur-gaine est i. Donner la relation entre i et r, et l’expression de cos(i) d’autre part.
  4. Exprimer le sinus de l’angle limite r entre les milieux n1 et n2
  5. Montrer que la propagation des rayons lumineux dans la fibre optique n’est permise que si q est inférieur à une valeur limite q 0 (à exprimer en fonction de n1 et n2).
corrigé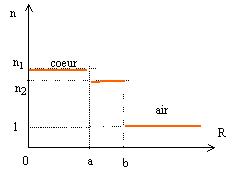

appliquer la loi de Descatres en I : nair sin q= n1 sin r.

avec nair = 1 ; sin q = n1 sin r.

Les angles i et r sont complémentaires : cos i = sin r

en J il y a réflexion totale si l' angle limite r vaut :

n1 sin i lim = n2 sin 90 = n2 ; sin i lim = n2 /n1.

sin2 i lim = [n2 /n1]2 ; cos2 i lim =1 -sin2 i lim = 1-[n2 /n1]2 ;

or cos i lim = sin r lim ; sin2 r lim = 1-[n2 /n1]2 ;

or sin r lim = sin q0/n1 ; sin2 r lim = sin2 q0/n21 ;

sin2 q0/n21 =1-[n2 /n1]2 ; sin2 q0=n21 *(1-[n2 /n1]2)= n21- n22.


retour -menu