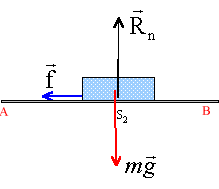
Un autoporteur (S₁)de masse m = 600 g est lancé depuis un point A avec une vitesse initiale V_A = 6 m.s^-1 sur un plan AB horizontal de longueur AB = 3 m sur lequel il glisse sans frottement, puis aborde un plan incliné BD, de longueur BD = 4 m, a = 30° par rapport à l'horizontale, sur lequel les frottements seront supposés négligeables. L'autoporteur pourra être considéré comme un solide ponctuel. On prendra g = 10 N.kg ^-1

1. Exprimer, puis calculer l'énergie cinétique de l'autoporteur en A.
2. Faire l'inventaire des forces extérieures agissant sur l'autoporteur (S₁) au cours de la phase AB.
   - Définir ces forces et les représenter sur le dessin.
   - Donner la définition d'un système pseudo-isolé.
   - L'autoporteur est -il pseudo-isolé au cours de la phase AB, dans la phase BD. En déduire la vitesse du centre d'inertie du mobile en B ?
3. Soit C le point de rebroussement sur le plan incliné.
   -Exprimer puis calculer le travail du poids de l'autoporteur et le travail de l'action R_n du plan sur l'autoporteur au cours du déplacement BC.
   - En appliquant la relation " travail- variation de l'énergie cinétique " pour le solide entre les instants t_B et t_C, en déduire BC la distance parcourue par le mobile avant de rebrousser chemin en C.
4. Un autre autoporteur (S₂) de masse m = 600g est lancé depuis un point A avec une vitesse initiale V_A = 6 m.s^-1 sur le plan AB horizontal . Au passage du point B il présente une vitesse V_B= 5,1 m.s^-1.
   -Le palet est-il pseudo-isolé sur la portion AB . Justifier la réponse.
   -Faire l'inventaire des forces extérieures agissant sur l'autoporteur (S₂).
   -Donner l'expression du travail de chaque force au cours du déplacement AB.
   - En appliquant la relation " travail- variation de l'énergie cinétique " pour l'autoporteur (S₂) entre les instants t_A et t_B, en déduire f la force de frottement supposée constante mise en jeu.

    

---

corrigé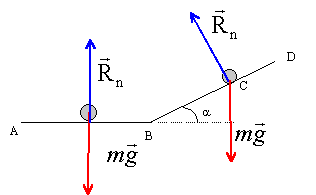

---

énergie cinétique initiale en A : ½mv_A² = 0,5* 0,6*6²= 10,8 J

sur le plan horizontal, le solide est soumis à son poids et à l'action du plan. En absence de frottement, ces deux forces se neutralisent et le solide est pseudo isolé. La vitesse du solide reste constante sur le parcours AB.

par contre sur le plan incliné le solide n'est pas pseudoisolé.

Ecrire que la variation d'énergie cinétique entre A et B est ègale à la somme des travaux des forces.

en A : ½mv_A²= 10,8 J; en C arrêt avant la descente donc pas d'énergie cinétique

variation d'énergie cinétique : énergie cinétique finale en C - énergie cinétique de départ en A

DE_cinétique = 0-10,8 = -10,8 J.

seul le poids travaille entre B et C car l'action du plan est perpendiculaire à la vitesse.

travail du poids lors de la montée BC : mg( z_B-z_C)

z_B: altitude de B, choisie comme origine

z_C = BC sin a = BC sin30 = 0,5 BC

d'où -10,8 = 0,6*10(0-0,5 BC) = -3 BC

BC= 10,8/3 = 3,6 m.

---

entre A et B la vitesse diminue, donc le solide S₂ n'est pas pseudoisolé.

Poids et action normale R_n du support sont perpendiculaires à la vitesse : elles ne travaillent pas.

travail de f: lors du déplacement AB : -f AB ou F AB cos 180

Ecrire que la variation d'énergie cinétique entre A et B est ègale à la somme des travaux des forces.

½ mv²_B-½mv²_A= -f AB

f = m/(2AB)(v²_A-v²_B) =0,6/ 6*(6²-5,1²)= 1 N.

---

---

Une automobile, de masse 1000 kg, descend une pente de 10%. La vitesse initiale du véhicule est de 90km. h^-1, les freins sont actionnés et exercent un effort (résultant) de freinage constant de 2500N.
- Déterminer la distance parcourue (x) avant arrêt.
- Quelle est la quantité d'énergie dissipée par le freinage ?

Une voiture monte une côte rectiligne de pente 6%. Elle possède une vitesse constante v=70km.h^-1 sur un parcours de longueur L=200m. Cette voiture tracte une caravane de masse m=500kg. Dans cet exercice, la caravane sera considérée comme un solide en translation.

Les forces de frottement, dues essentiellement à la résistance de l'air, s'opposent au mouvement de la caravane. On admettra qu'elles sont équivalentes à une force unique et constante f de même direction que le vecteur vitesse de valeur f=400 N.

1. Faire le bilan des forces extérieures s'appliquant à la caravane.
2. Que peut-on dire de la somme vectorielle F de ces forces? Citer la loi qui perment de l'affirmer. 
3. En appliquant le théorème de l'énergie cinétique au système caravane, calculer le travail de la force T pour le déplacement de longueur L. En déduire la valeur de T.

Le curling est un sport joué sur la glace avec des"stones"(pierres rondes). La masse d'une stone est m=19,86 kg. Le jeu consiste à envoyer la stone au plus près du centre d'une cible situé à 38,43m du joueur. Le joueur lance la stone à la vitesse de 0,67 m/s: elle s'arrête au centre de la cible.

1. Calculer l'énergie cinétique de la stone au moment où le joueur lâche la poignée de la stone.
2. Calculer le travail des forces de frottement.
3. On admet que toute l'energie mécanique perdue par frottement est consommée par la fonte de l'eau solide (glace). Calculer la masse de la glace fondue. On donne la chaleur latente de fusion de la glace L_f=335 kJ/kg

On fixe une masse m=89 g à l'extrémité d'un fil de longueur L=1,57m. On écarte le fil de sa position d'équilibre d'un angle a=25°. Après 2 min 30s d'oscillations, l'écart angulaire maxi du fil et de la verticale n'est plus que b =17°. Après 6 min 42s le pendule est considéré comme immobile.(pour exprimer l'énergie potentielle de pesanteur, on choisit comme niveau de référence le plan horizontal passant par le centre de gravité de la masse à l'équilibre)

1. Calculer l'enerqie mécanique du pendule
   - à l'instant du lâcher.
   - lorsque le pendule s'est immobilisé.
2. Calculer le travail des forces de frottement
   - du lâcher du pendule à son immobilisation
   - pendant la durée t=2 min 30s comptée à partir de l'instant du lâcher.

---

corrigé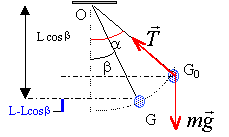

---

énergie cinétique initiale nulle (pas de vitesse)

énergie potentielle de pesanteur initiale mgL(1-cosa)

énergie mécanique initiale : mgL(1-cosa)

E_{M init} =0,089*9,8*1,57(1-cos25)= 0,128 J.

à l'arrêt à la verticale du point de fixation O, l'énergie mécanique est nulle( pas de vitesse et on se trouve à l'origine des altitudes)

le travail des frottements correspond à la diminution de l'énergie mécanique.

du lâcher du pendule à son immobilisation ce travail vaut -0,128 J.

pendant la durée t=2 min 30s comptée à partir de l'instant du lâcher :

lorsque b =17° l'énergie mécanique se trouve entièrement sous forme potentielle de pesanteur

E_M = mgL(1-cosb) = 0,089*9,8*1,57(1-cos17)= 0,06 J.

diminution de l'énergie mécanique = travail des frottement = 0,06-0,128 = -0,068 J.

---

Un enfant de masse m_e=35 kg glisse sur une luge de masse m_l=10 kg le long d'une pente inclinée de 30°. Dans un 1^er temps, les forces de frottement sont négligées. On s'intéresse au mouvement du système S (luge + enfant) entre le point A, où la luge passe à l'instant t_A à la vitesse v_A et le point B, où la luge passe à l'instant t_B à la vitesse v_B. Distance AB: d=150m

1. Calculer le travail W(P) du poids du système S et le travail W(R) de la réaction R du sol.
2. Calculer la variation DEc de l'énergie cinétique Ec du système entre A et B.
3. Calculer la variation D Ep de l'énergie potentielle de pesanteur Ep du système entre A et B.
4. Calculer la variation D Em de Em=Ec+Ep. Commentez.
   On suppose maintenant que le sol exerce une force de frottement sur la luge. La réaction R du sol comporte une composante normale N et une composante tangentielle T.
5. Exprimer D Ec en fonction du travail W(T) de T
6. En déduire la variation D Em de Em=Ec+Ep en fonction de W(T).
   - Montrez que D Em<0. Commentez.

Une automobile de masse m=800 kg descend une route de pente 10% (pour 100 m parcourus l'altitude diminue de 10 m ). La vitesse initiale du véhicule est v_i = 90 km/h . Les freins exercent une force constante de valeur F = 2500 N . On néglige l'action de l'air.

1. Comment évolue l'énergie mécanique du véhicule lors de la descente ?
2. Déterminer la distance parcourue par le véhicule jusqu'à l'arrêt en fonction de v_i, m, F et g .