|
première S |
||||||
|
||||||
|
|
corrigé Umax = Ueff * racine carrée (2) = 24*1,414 = 34 V Ueff=RIeff soit Ieff =24/0,96 =25 A puissance P= Ueff Ieff = 24*25= 600 W 1h 25 min = 3600 + 25*60 = 5100 s énergie 5100*600 = 3 10 6 joules Uc = Ueff = 24 V débit : 6 / 60 = 0,1 L /s soit 0,1 kg d'eau élevé de 1,2 m par seconde l'énergie potentielle de cette masse d'eau augmente de : mgh = 0,1*9,8*1,2 = 1,176 J à chaque seconde puissance mécanique mise en jeu par la pompe : 1,176 watt. puissance mécanique mise en jeu par le moteur : 1,176 / 0,2 = 5,88 W puissance électrique recue par le moteur : 5,88 / 0,85 = 6,92 W perte par effet joule au niveau du moteur : 6,92 *0,15 = 1,04 W or P joule = r I², en divisant la puissance perdue par effet joule par l'intensité du courant qui traverse les bobinages du moteur, on trouve la résistance interne du moteur.
|
|||||
|
Dans un moteur électrique, le fils actifs sont placés suivant les génératrices d'un cylindre de rayon r = 8 cm. Chaque fil de longeur L = 15 cm est parcouru par un courant I = 10 A et est soumis à une induction radiale de valeur B = 1,2 Teslas. - Calculer la valeur F de la force qui agit sur chaque fil actif. - Quel est le travail W de cette force quand le cylindre fait un tour? - Le moteur comprend n= 700 fils actifs. Calculer le travail total Wt pour un tour. - Sachant que le moteur tourne à N = 1800 tr/mn, quelle est sa puissance ?
corrigé force de Laplace sur un fil : F= BIL = 1,2*10*0,15 = 1,8 N travail de cette force tangentielle, colinéaire à la vitesse 1 tour = 2 pi rayon du cylindre =2*3,14*0,08 = 0,5024 m travail W= 1,8* 0,5024 = 0,904 J pour tous les fils : 700*0,904 = 633 J 1800 / 60 = 30 tours / s puissance : 633*30= 19 kW autre méthode : 1800/60 = 30 tours/seconde vitesse angulaire = 2*3,14*30 = 188,4 rad/s couple : 1,8*2*0,08 = 0,288 Nm pour deux fils diamètralement opposés pour les 350 couples de fils : 350*0,288 = 100,8 Nm puissance : 100,8*188,4= 19 kW
|
||||||
|
corrigé puissance électrique reçue par le moteur P=UI=12*10=120 W 110 tours/min = 110 /60 = 1,833 tr/s vitesse angulaire w= 2*3,14*1,833 = 11,51 rad/s Puissance mécanique : 11,51*10 =115,1 watts rendement = P
mécanique / P électrique reçue =115,1 /120 = 0,96.
diviser la puissance en watt par 220 V exemple 3000 / 220=13,6 A puissance (kilowatt) fois durée de fonctionnement (heure) = énergie (kilowattheure) puissance = énergie /durée=37,2 / 24 = 1,55 kW = 1550 watts puissance (watt) = tension efficace (220 V) fois intensité efficace(A) I= 1550 / 220 = 7 A
|
||||||
|
corrigé puissance (W) = tension efficace (V) * intensité (A) =230*8,7= 2000 W = 2 kW intensité dans le filament : puissance (W) / tension (V) = 6/6 = 1 A. puissance maximale : 230*20 = 4 600 W = 4,6 kW au delà le fusible fond et coupe le courant. 3 + 1,2 k + 2,1 =6,3 kW on ne peut pas brancher
simultanément ces trois appareils.
We = U*I*t = P*t= 1800*6*3600= 3,89.107 joules Wc =Ceau*m*(Tfinale-Tinitiale) 150 L d'eau ont une masse de 150 kg Wc = 4,18.103*150*50 = 3,13.107 joules We est supérieure à Wc. la différence correspond à l'énergie transférée au milieu extérieur : 3,89.107 -3,13.107 = 7,6 107 J.
|
||||||
|
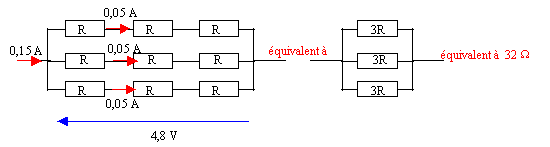
On veut alimenter une DEL à l'aide d'un générateur de f.é.m E=6,0V et de résistance interne négligeable. En fonctionnement normal, la del maintient entre ses bornes une tension U=1,2V et l'intensité qui la traverse ne doit pas dépasser 150 mA.
corrigé Les tensions aux bornes de la DEL et du résistor en série vont s'ajouter tension aux bornes du résistor U= RI d'où 1,2 + RI= 6 soit R= (6-1,2) / I = 4,8 /I l'intensité maximale est 0,15 A, au delà on casse la diode par effet joule. valeur minimale de R= 4,8 / 0,15 = 32 W. Pmax 0,25 = tension aux bornes du résistor (4,8 V) fois intensité traversant le résistor. d'où l'intensité maximale admissible : I= 0,25 / 4,8 =0,052 A. les résistors seront détruits si l'intensité dépasse 52 mA ; or l'intensité peut atteindre 150 mA on ne peut donc pas placer un résistor de 32 ohms en série avec la diode. Par contre on peut associer ces résistor en dérivation.
|
||||||
|
corrigé 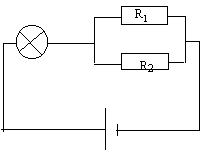
résistance équivalente à R1 et R2 en dérivation Réqui = R1 R2 /(R1+R2)=22*47 / (22+47) = 15 W. résistance de la lampe : r = u / i=6/0,1 = 60 W. résistance totale du circuit : 60 +15 = 75 W. tension aux bornes de la lampe pour un fonctionement nominal : 6 V intensité du courant dans le filament de la lampe : 6/ 60 = 0,1 A tension aux bornes des résistances en dérivation : 15*0,1 = 1,5 V tension aux bornes du générateur : 1,5+6= 7,5 V. intensité dans chaque résistance 1,5/22 = 0,068 A et 1,5/47 =0,032 A puissance dissipée dans chaque résistance : tension * intensité qui la traverse 1,5*0,068 =0,102 W et 1,5*0,032 = 0,048 W l'intensité du courant est satisfaisante, la puissance reste inférieure à 1W. La puissance chimique est convertie en puissance électrique et en puissance thermique. Pchim = Pelec + Pjoule. EI= UI +rI² ; Pelec = EI -rI² Pelec = 0 si I=0 : le circuit électrique est ouvert Pelec = 0 si EI=rI² soit I=E/r = 8/4= 2A: le générateur est en court circuit et toute la puissance chimique est convertie en puissance thermique.
|
||||||
|
corrigé I1 = E/ ( somme des résistances en série) =7,8/(4,2+12) = 0,48A Chercher la résistance équivalente de l'ensemble : 4,3 W et 12 W en série équivalentes à 12+4,3 = 16,3 W 16,3W et 9,1W en dérivation équivalentes à : 16,3*9,1/(16,3+9,1)= 5,84 W I2 = 7,8/(4,2 + 5,84) = 0,78 A. |
||||||
|
Un accumulateur au plomb de camion possède une fem E=24.0V et une résistance interne r =0,180 ohm. On oriente l'accumilateur de sa borne négative N vers sa borne positive P, et on note I l'intensité du courant qui le traverse en supposant I positive.
corrigé UPN = E-r I Pelec = EI-rI² 700 = 24 I-0,18 I² résoudre : 0,18 I²-24 I+700 = 0 D=24²-4*0,18*700=72; racine carrée (72)= 8,48 I1=(24+8,48)/(2*0,18)= 90 A I2=(24-8,48)/(2*0,18)= 43,1 A puissance dissipée par effet joule : rI² 0,18*90²= 1458 W impossible car supérieur à 700 W, donc la valeur I=90 A n'est pas à retenir. 0,18*43,1² = 334,4 W énergie dissipée par effet joule en 10 min = puissance (W) * durée (seconde) 334,4*600 =200 400 J. diminution de l'énergie chimique en 10 min : E I t = 24*43,1*600 = 620 640 J. tension aux bornes de l'accumulateur : UPN= 24-0,18 *43,1 = 16,2 V. |
||||||
|
La résistance interne d'une petite génératrice, mesurée grâce un ohmètre, est r = 0,800 ohm. L'axe horizontal de la génératrice est relié à une poulie. Une masse de 300 g est suspendue à un fil enroulé dans la gorge de la poulie. On prendra g=9,81 N/Kg. Les bornes de la génératrice sont connectées à une résistance de la valeur R=3 ohms. La masse m est lachée sans vitesse. Rapidement, elle prend une vitesse constante v=18 cm/s. L'étude des variations et transfetrs d'énergie sera effectuée pour une durée D t=10 s, au cours de laquelle m descend d'une hauteur h.
corrigé Le travail recu par le système (génératrice poids) est celui de la force extérieure au système, constituée par le poids de la masse m. Soit W = mgh = mg v Dt D t en secondes, m en kg, v en m/s donc W en joules W= 0,3*9,81*0,18*10= 5,3 J. La tension aux bornes de la génératrice est : UPN = E - rI La puissance disponible aux bornes de la génératrice est : UPN *I l'énergie disponible aux bornes de la génératrice = puissance (W)= durée (seconde) Wdisponible = UPN I Dt = (EI-rI²) *Dt = EI Dt-ri²Dt L'énergie reçue par la résistance R alimentée par le générateur est WR = R I²Dt écrire que WWdisponible = WR EIDt-ri²Dt = R I²Dt EI-rI²=RI² ; EI= (R+r) I² = mgh le membre de gauche représente l'énergie transformée en chaleur par effet Joule durant l'intervalle Dt dans R et dans r le membre de droite représente l'énergie potentielle perdue par la masse m pendant ce temps. Dans le système
(génératrice, masse Terre) il y a conversion d'énergie mécanique en
énergie calorifique mais sans perte.
E=mgh / I = 5,3 / 1,18 = 4,5 V. UPN = E - rI = 4,5-0,8*1,18 = 3,56 V.
|
||||||
|
On associe en série une batterie d'accumulateurs (de f.é.m E=18V et de résistance interne r =1,2 ohms), une résistance de valeur R=4,8 ohms, un moteur (de f.é.m E' et de résistance interne r') et un ampèremètre de résistance négligeable.
corrigé Le moteur bloqué se comporte comme un résistor ( il va chauffer) tension aux bornes de la batterie : Ubat = E-rI tension aux bornes du moteur bloqué : Umot bloqué = r' I tension aux bornes du résistor uR= R I moteur et résistor en série donc : Ubat =Umot bloqué + uR. E-rI = r'I + R I
soit r' = E/I-r-R = 18/1,2 -1,2 -4,8= 9 W.
Ubat =Umot + uR ; E-rI =E'+ r'I + R I d'où I = (E-E') / (R+r+r') E' = E-I(R+r+r')= 18-1*(4,8+1,2+9)= 3 V. puissance consommée par le moteur : Pmot = (E'+r'I) I = (3+9*1)*1 = 12 W puissance consommée par le résistor PR= RI² =4,8*1² = 4,8 W. puissance utile = puissance mécanique = E'I = 3*1 = 3 W puissance électrique fournie au circuit : (E-rI)I = (18-1,2*1 )*1=16,8 W rendement du circuit = puissance mécanique utile / puissances recues par le circuit 3 / 16,8 = 0,18 ( 18 %) rendement du moteur = puissance mécanique utile / puissance recue par le moteur 3 / 12 = 0,25 ( 25 %)
|
||||||
|
Un moteur a les caractéristiques suivantes : résistance interne r' = 11 W f.e.m E' = 7,2 V. Il est alimenté par un générateur de tension pour lequel E = 16,0 V et r = 1,2 W.
corrigé 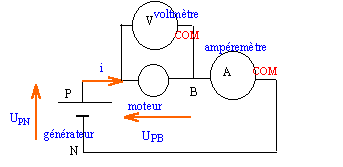
UPN= E-ri ; UPB= E'+ r'i; la tension est presque nulle aux bornes de l'ampéremètre UPN +UPB= 0 ;E-ri +E'+ r'i = 0 soit i =(E-E') / (r+r') i =(16-7,2)/ (11+1,2) = 0,72 A. puissance électrique Pe reçue par le moteur : uPB
i = E'i+ r'i²= 7,2*0,72
+ 11*0,72² = 10,9
W énergies mises en jeu : 2 h 45 min = 2*3600+45*60 =7200+2700=9900 s. énergie électrique consommée par le moteur : PeD t = 5,8*9900 =57,42 kJ énergie mécanique :PmD t = 5,18*9900 =51,28 kJ énergie thermique :PmD t = 6,32*9900 =62,57 kJ. rendement du {moteur- alternateur}=(Pm - Pint ) / Pe = 0,18 Pm - Pint = 0,18 Pe ; Pint
= Pm -0,18 Pe =5,18-0,18*5,8= 4,14 W.
|
||||||
|
En TP, on envisage d'associer en série un générateur ( E = 9,0 V ; r = 1,2 W ) et deux conducteurs ohmiques marqués respectivement ( R1 = 33 W ; 0,25 W ) et ( R2 = 82 W ; 0,50 W ). Les puissances indiquées sont les puissances maximales admissibles par les conducteurs ohmiques. Au-delà de cette valeur, ils risquent d'être détériorés.
corrigé 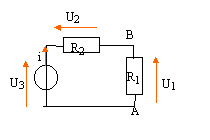
intensité : I= E / (r+R1+R2)=9/(1,2+33+82)= 0,077 A. puissance dissipée dans R1 : R1 I² = 33*0,077²= 0,2 W ; dans R2 :R1 I² = 82*0,077²= 0,49 W ; Ces valeurs étant
inférieures aux puissances 0,25 W et 0,5 W, les résistors ne seront pas
grillés si on réalise ce montage.
les conductances s'ajoutent : G1 = 1/R1 = 1/33 =0,03 S ; G2 = 1/R2 = 1/82 =0,0122 S ; G= G1 + G2 = 0,03+0,0122 = 0,0422 S la résistance équivalente aux résistances du circuit est :Réqui=
1/0,0422 = 23,7 W. tension aux bornes des résistors : E-ri = 9-1,2*0,36 = 8,57 V 8,57 = R1i1 soit i1 = 8,57 / 33 = 0,26 A. 8,57 = R2i2 soit i2 = 8,57 /
82 = 0,10 A. dans R1 : 8,57*0,26 = 2,2 W ( donc résistor grillé) dans R1 : 8,57*0,1 = 0,85
W ( donc résistor grillé)
|
||||||
|
Un nouveau type de lampe d'éclairage permet selon leurs fabricants de faire des économies d'énergie. Le slogan publicitaire qui se résume par " 20 W = 100 W " signifie que cette lampe consomme une puissance de 20 W et éclaire aussi bien qu'une lampe à incandescence ordinaire de puissance nominale 100 W. La durée de vie moyenne de cette nouvelle lampe est en général supérieure à 3 ans pour une utilisation de 3 heures par jour alors que les lampes traditionnelles, dans les mêmes conditions d'utilisation, ont une durée de vie d'environ 1 an.
corrigé énergie (kWh) = puissance (kW) * durée ( h) lampe à économie d'énergie : 0,02*3*365*3=65,7 kWh coût : 0,0929292 * 65,7 = 6,10 €. lampe incandescence : 0,1*365*3= 109,5 kWh coût : 0,0929292 * 109,5 = 10,17 €. économie : 4,07 €.
|
||||||
|
|