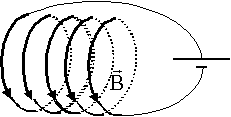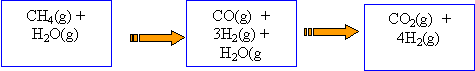Aurélie jan 04

champ magnétique - force de Laplace - énergie de liaisons

devoir commun première S




Google



 

  1. Le conducteur rectiligne AB est parcouru par un courant continu et plongé dans le champ magnérique B.
    - Quels sont la direction et le sens de la force de Laplace à laquelle il est soumis : donner la réponse par une phrase, puis représenter cette force sur le schéma.
  2. Une tige de cuivre peut rouler sur des rails de cuivre horizontaux. L'ensemble est alimenté en courant continu. La tige se déplace vers la droite. Représenter le vecteur champ magnétique auquel elle est soumise et donner la réponse par une phrase.
    - Calculer la valeur de l'intensité de cette force lorsque le champ magnétique a une valeur de 0,2 T, le courant une intensité de 10 A, et que l'écartement des rails est de 8 cm.
  3. Une bobine circulaire est placée dans l'entrefer d'un aimant de haut-parleur (voir figure ci-contre, vue de dessus ou en coupe : N et S représentent les pôles de l'aimant). La bobine est parcourue par un courant continu dans le sens indiqué par la flèche.
    - Représenter le vecteur champ magnétique B au point M sachant qu'il est radial (c'est-à-dire porté par les rayons du cercle), ainsi que la force de Laplace F qui s'exerce sur une portion de circuit de la bobine au point M.
  4. Représenter le vecteur champ magnétique à l'intérieur du solénoïde ci-contre parcouru par un courant.
    - Indiquer les noms des faces du solénoïde.
    - Calculer l'intensité de ce champ sachant que le solénoïde mesure 25 cm, qu'il comporte 200 spires et qu'il est parcouru par un courant constant d'intensité 2 A. On donne la constante de perméabilité magnétique du vide (et de l'air) : µ0 = 4p.10-7 SI
  5. À quelle époque Laplace vivait-il ? Citer trois domaines des sciences dans lesquels il a effectué des travaux remarquables (en dehors de l'électromagnétisme).
  6. Un cadre rectangulaire indéformable ABCD est formé par un fil conducteur enroulé sur du carton. Le fil peut être relié à un générateur. L'enroulement comporte 100 spires rectangulaires bobinées sur le carton. Il est suspendu à un dynamomètre. Sa partie horizontale inférieure AB est immergée dans un champ magnétique uniforme B horizontal, orthogonal à AB et dirigé vers l'avant.
    - Montrer que les forces électromagnétiques agissant sur les portions CB et DA immergées dans le champ magnétique sont opposées, quel que soit le sens du courant dans l'enroulement.
    - Lorsque l'intensité I du courant dans l'enroulement est nulle, le dynamomètre indique 1,9 N. Pourquoi ?
    - On fait passer un courant d'intensité I = 10,0 A : le dynamomètre indique 2,5 N. Déterminer la valeur de la force électromagnétique qui agit sur la portion AB du cadre, ainsi que la direction et le sens de cette force, et le sens du courant.
    - Quelle sera l'indication du dynamomètre si l'on inverse le sens du courant ? Justifier.
 

 

 

 

 


corrigé
Le conducteur traversé par un courant d'ntensité I et placé dans un champ magnétique non colinéaire à AB est soumis à la force de Laplace F. Cette force est perpendiculaire au plan défini par AB et le vecteur champ magnétique B. Son sens est donné par la règle des 3 doigts de main droite .( pouce : courant ; index : champ ; majeur : force )

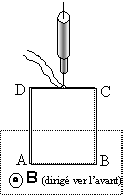
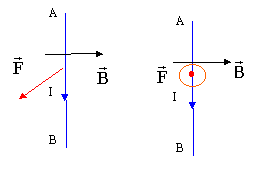
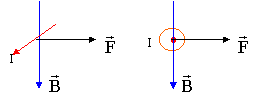
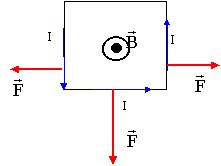
On applique la même règle :

d'après les bornes du générateur le courant I vient vers l'avant ; la force F est horizontale vers la droite d'après le déplacement de la tige.

valeur de F : F= I L B sin 90 = 10*0,08*0,2 = 0,16 N

Le champ B est radial, donc dirigé selon un rayon, et dans le sens de N ves S (convention sur les champs magnétiques).

la force est perpendiculaire au plan défini par le champ et le courant et dirigée vers l'avant de la figure.

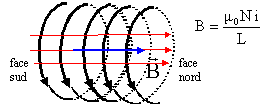
B= 4*3,14 10-7 * 200 * 2 / 0,25 = 2 mT.

Laplace : 1749 - 1827 (fin XVIIIe début XIXe siècle)

Trois domaines des sciences dans lesquels il a effectué des travaux remarquables : la mécanique céleste (application des lois de Newton au mouvement des planètes), calcul des probabilités, incertitudes sur les mesures physiques, cosmologie (origine du système solaire dans la " nébuleuse de Laplace "), analyse mathématique (opérateur laplacien).

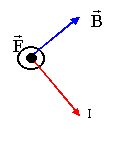
le dynamomètre indique 1,9 N : c'est le poids du cadre.

le dynamomètre indique 2,5 N : la force électromagnétique qui agit sur la portion AB du cadre, est donc verticale vers le bas et vaut 2,5 - 1,9 = 0,6 N.

si l'on inverse le sens du courant, le sens de F change mais pas sa direction ni sa valeur : elle sera verticale vers le haut. Le dynamomètre indiquera 1,9 - 0,6 = 1,3 N.

production d'hydrogène :

Le dihydrogène est un produit industriel très utilisé. Un des procédés employé pour le produire est le " reformage du gaz naturel par la vapeur d'eau ". Il se déroule en deux étapes représentées par les équations chimiques (1) et (2). L'équation (3) est le bilan représentant la transformation globale.

Équation (1) : CH4(g) + H2O(g) --> CO(g) + 3H2(g) Q1

Équation (2) : CO(g) + H2O(g) --> CO2(g) + H2(g) Q2

Équation (3) : CH4(g) + 2H2O(g) --> CO2(g) + 4H2(g) Q3

  1. Calculer l'énergie molaire de réaction Q1.
  2. Calculer l'énergie molaire de réaction Q2.
  3. Calculer l'énergie molaire de réaction Q3.
  4. On se propose de vérifier que si une réaction est la somme de réactions successives, son énergie molaire de réaction est la somme des énergies molaires des réactions successives. Vérifiez cette affirmation sur l'exemple précédent.
  5. Représenter les transformations successives en remplissant des rectangles contenant le système de départ, le ou les systèmes intermédiaires et le système final : (un système chimique est l'ensemble des substances présentes au moment considéré, affectées de leur nombre de moles)

énergie de liaison en kJ/mol : DC-H= 410 ; DCO= 1090 dans CO ; DC=O= 798 ( dans CO2); DO-H= 460 ; DH-H= 436 ;

DC-O= 356

corrigé
énergie molaire d'une réaction = somme des énergies de liaison des liaisons cassées - somme des énergie de liaison des liaisons formées.

Q1 = 4DC-H + 2DH-O - DCO - 3DH-H = 4×410 + 2×460 - 1090 - 3×436 = 162 kJ/mol.

Q2 = DCO + 2DH-O - 2DC=O - DH-H = 1090 +2×460 - 2×798 - 436 = -22 kJ/mol.

Q3 = 4DC-H + 4DH-O - 2DC=O - 4 DH-H = 4×410 + 4×460 - 2×798 - 4×436 = 140 kJ/mol.

 

On vérifie que Q3 = Q1 + Q2 ; les équations chimiques vérifient (1) + (2) = (3) lorsqu'on fait la somme membre à membre des équations 1) et (2) on obtient l'équation (3).

Un système chimique est l'ensemble des substances présentes au moment considéré, affectées de leur nombre de moles :

Le méthanol CH3OH est un liquide qui bout à 64,5 °C sous la pression atmosphérique normale. À cette température il faut lui fournir 37,4 kJ/mol pour le vaporiser.

  1. Quelle énergie faut-il fournir à une mole de méthanol liquide pour élever sa température de 25 °C à 64,5 °C ? On donne la chaleur molaire du méthanol c = 81,6 kJ/°C/mol.
  2. Quelle est l'énergie mise en jeu pour vaporiser, à la pression normale, une mole de méthanol pris à 25 °C ?
  3. Déterminer l'énergie de cohésion de la molécule de méthanol à 25 °C, en kJ/mol.
  4. Comparer les énergies de cohésion intermoléculaire et intramoléculaire du méthanol.

     

corrigé
énergie faut-il fournir à une mole de méthanol liquide pour élever sa température de 25 °C à 64,5 °C ?

Q1 = n. c. Dq = 1×81,6×(64,5 - 25) = 81,6×39,5 = 3 223 kJ.

énergie mise en jeu pour vaporiser, à la pression normale, une mole de méthanol pris à 25 °C :

Q2 = 3 223 + 37,4 = 3260 kJ

énergie de cohésion de la molécule de méthanol à 25 °C, en kJ/mol ( 3liaisons C-H ; une liaison C-O et une liaison O-H)

d'où E = 3DC-H + DC-O + DH-O = 3×410 + 356 + 460 = 2046 kJ/mol.

Comparaison des énergies de cohésion intermoléculaire et intramoléculaire du méthanol :

l'énergie intermoléculaire de cohésion du méthanol liquide est son énergie de vaporisation (pour une mole) : 37,4 kJ ;

l'énergie intramoléculaire de cohésion du méthanol est celle calculée à la 3ème question : 2046 kJ (pour une mole).

Leur quotient vaut : 2046 / 37,4 = 54,7 . La 2ème est 54,7 fois plus grande que la 1ère .

retour -menu