|
première S |
||||||
|
||||||
|
|
Un générateur idéal de fem E = 12 V est utilisé pour alimenter le pont de résistances représenté ci-contre :R1 = 20 W ; R2 = 5,0 W ; R3 = 15 W ; R4 = 60 W. 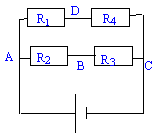
corrigé R1 et R4 en série, équivalent à : R5= R1+R4 = 20+60 = 80 W. R2 et R3 en série, équivalent à : R6= R2+R3 = 5+15 = 20 W. R5 et R6 en dérivation, équivalent à : R= R5R6 / (R5+R6 )=20*80 / (20+80)= 16 W. I1 = E/ R5= 24/80 =0,3 A ; I2 = E/ R6= 24/20 =1,2 A ; puissance consommée dans R1 et R4 : E I1 = 24*0,3 = 7,2 W puissance consommée dans R2 et R3 : E I2 = 24*1,2 = 28,8 W puissance fournie par le générateur : E(I1+I2)= 24*1,5= 36 W UAD= R1I1 = 20*0,3 = 6 V ; UDC= R4I1 = 60*0,3 = 18 V ; UAB= R2I2 = 5*1,2 = 6 V ; UBC= R3I2 = 15*1,2 = 18 V ; UBD= UBA+ UAD= -UAB+ UAD -6+6= 0.
|
|||||
|
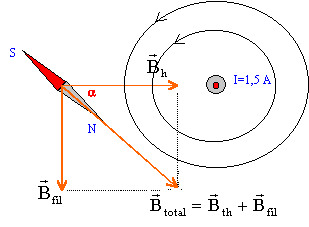
On place un fil de cuivre vertical en face du pôle nord d'une boussole horizontale orientée dans le champ magnétique terrestre. Lorsqu'on fait circuler un courant d'intensité 1,5 A dans le fil, on constate que la boussole est déviée d'un angle a= 45 ° par rapport à sa position initiale. 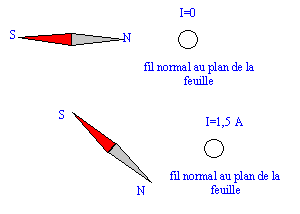
corrigé 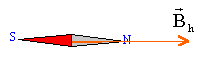
les lignes de champ magnétique créées par le courant électrique traversant le fil sont des cercles concentriques
valeur du champ crée par le courant : tan a = Bfil/Bh =1 car a=45°. Bfil=Bh = 20 mT. si l'intensité est égale à 5 A alors B'fil = 5/1,5 Bfil = 3,33 Bfil . tan a '= B'fil/Bh = 3,33 Bfil/Bh = 3,33 d'où a '= 73,3°.
|
||||||
|
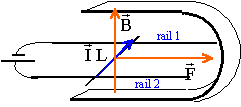
Deux rails conducteurs rectilignes sont disposés horizontalement comme indiqué sur la figure. Ils sont distants de L=10 cm. Une tige de cuivre de masse m=20 g est libre de se déplacer sur ces deux rails et assure le contact électrique. L'ensemble est placé à l'intérieur d'un aimant en U qui crée un champ magnétique uniforme B vertical et de valeur B=100 mT. 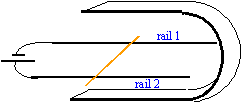
corrigé Le conducteur mobile sur les rails, traversé par un courant I et placé dans le champ magnétique B est soumis à une force de Laplace F= I L B, perpendiculaire au plan défini par le conducteur et le champ.
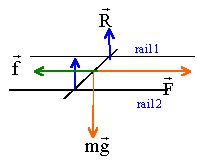
F= I L B= 2 *0,1*0,1 = 0,02 N. La tige est également soumise à son poids P, à l'action des rails R et aux frottements f.
le poids et l'action des rails, perpendiculaires à la vitesse ne travaillent pas. travail moteur de F : Wmot = 0,02*0,02 = 4 10-4 J les frottements sont négligés. la variation d'énergie cinétique est égale au travail de la force de Laplace Ecfin-Ec init = 2 10-4 = ½mv²fin. vfin = racine carrée (2*2 10-4 / 0,02) =0,14 m/s. la tige se déplace dans le plan horizontal : l'énergie potentielle de pesanteur ne varie pas. Le mouvement de la tige est rectiligne uniforme : la tige est pseudo-isolée le poids et l'action des rails sont opposées la force de Laplace et les frottements sont opposés. d'où f= 0,02 N.
|
||||||
|
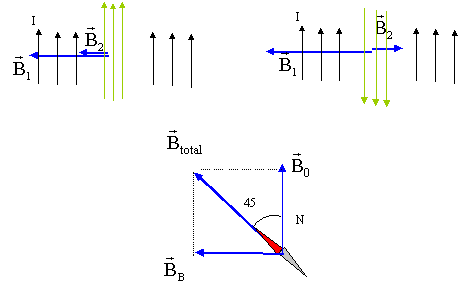
On dispose d'un solénoïde de longueur 50cm et comportant 200 spires et d 'une bobine plate comportant 20 spires de rayon 12,5cm. Le solenoide est placé dans la bobine de facon que leurs axes et leurs centres soient confondus. L'axe commun des deux bobines est perpendiculaires au plan meridien magnetique. On place une petite aiguille aimantée au centre commun O et on branche le solénoïde et la bobine en serie dans un circuit parcouru par un courant dintensite I . L'aiguille aimantée dévie alors de 45 degrés. Montrer que 2 cas sont possibles. Déterminer dans chaque cas l'intensite du courant. Données : champ crée au centre de la bobine plate de rayon r : B= Nm0I/(2r) ; N nombre de spires composante horizontale du champ terrestre B0 =2 10-5 T corrigé deux possibilités : le champ du solénoide s'ajoute ou se retranche à celui de la bobine, tout dépend du sens du branchement les deux bobines en série sont traversées par la même intensité I
la boussole s'oriente suivant le champ total l'angle faisant 45 °, tan 45 = 1; champ total des bobines = champ terrestre = 2 10-5 T solénoide : m0 nI avec n=N/L= 200/0,5 = 400 spires par mètre. Bsolénoide = 4*3,14 10-7 * 400 I = 5 10-4 I bobine plate : Bbob= Nm0I/(2r) =20*4*3,14 10-7 * I / (2*0,125)=10-4 I champ total des bobines: 6 10-4 I = 2 10-5 soit I= 0,033 A. ou 4 10-4 I= 2 10-5 soit I= 0,05 A.
|
||||||
|
|