On mesure la conductance G de V₁= 100 mL d'une solution S₁ d'acide éthanoïque de concentration C₁=1 mol/L : G= 1,6 mS. La surface des électrodes de la cellule est S= 1 cm² et leur distance est d= 1cm.

Le pH d'une solution S₂ d'hydroxyde de sodium ( V₂= 100 mL) vaut pH=13. On mélange les deux solutions.

Conductivité molaire ionique à 25 °C en S m² mol^-1 : l_CH3COO- = 5 ; l_H3O+ = 35 ; l_Na+ = 5 ; l_HO- = 20 .

pKa (CH₃COOH/CH₃COO^-)=4,8 ; Ka(CH₃COOH/CH₃COO^-)=1,6 10^-5.

1. Ecrire l'équation chimique de la réaction entre l'acide éthanoïque et l'eau.
   - Etablir le tableau d'avancement et déterminer l'avancement maximal.
   - A partir de la mesure de la conductance, calculer la concentration des ions présents dans la solution S₁.
   - En déduire le taux d'avancement final et conclure.
2. Calculer la concentration C₂ de la solution S₂.
   - Cette solution a été préparée à partir d'une solution d'hydroxyde de sodium de concentration C=0,5 mol/L. Expliquer le protocole opératoire à suivre pour réaliser S₂. Nommer la verrerie.
3. Ecrire l'équation chimique de la réaction acido-basique qui a lieu entre l'acide éthanoïque et l'ion hydroxyde.
   - Calculer la constante d'équilibre K de cette réaction.
   - Faire l'inventaire des espèces chimiques présentes à l'état final dans la solution et calculer la concentration finale de l'acide éthanoïque et de sa base conjuguée.

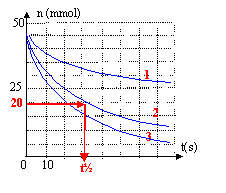
Dans une enceinte fermée, la réaction du dioxyde de soufre sur le dioxygène donne du trioxyde de soufre. Ces trois gaz se comportent comme des gaz parfaits. La réaction est considérée comme totale. Les courbes suivantes donnent les variations de quantités de matière en fonction du temps. Les quantités initiales n₀(SO₂) et n₀(O₂) sont égales. La courbe 2 correspond au dioxyde de soufre. On note t½ le temps de demi réaction.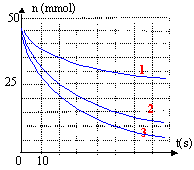

 

Répondre par vrai ou faux : réponse exacte = +0,5 point ; réponse fausse = -0,5 point ; pas de réponse = zéro

1. Le mélange est stoechiométrique.
2. la quantité de matière maximum de trioxyde de soufre formé est 0,02 mol.
3. Après retour à la température de départ la pression a retrouvé sa valeur initiale.
4. La courbe 3 représente l'évolution de la quantité de matière de dioxygène au cours du temps.
5. Aucune des trois courbes ne donne l'avancement de la réaction en fonction du temps.
6. La vitesse de la réaction est nulle à t=0.
7. Le coefficient directeur de la tangente à la courbe 2 à la date t=20 s est égal à la valeur de la vitesse de réaction à cette date.
8. La valeur de t½ est voisine de 30 s.

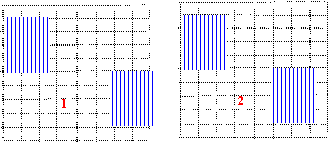
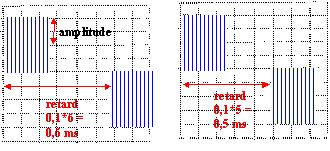
répondre vrai ou faux aux 10 questions suivantes : 1 point par question ; une erreur ou une absence de réponse enlève 0,25 pt ;deux erreurs conduisent à zéro pur la question.

1. Propagation d'une onde mécanique progressive :
   a- La propagation s'accompagne d'un transfert de matière.
   b- La propagation s'accompagne d'un transfert d'énergie.
   c-La vitesse de propagation dépend de la rigidité du milieu.
   d- On appelle retard la durée qui sépare l'émission de deux ondes successives.
   b et c sont vraies.
2. Propagation d'une onde mécanique périodique sinusoïdale
   a- Deux points distants d'un nombre entier de longueur d'onde vibrent en phase
   b- Deux points quelconques du milieu de propagation ont des trajectoires de même nature.
   c- La trajectoire d'un point situé à une longueur d'onde de la source est une sinusoïde.
   d- La longueur d'onde est la durée au bout de laquelle un point donné revient à sa position de départ.
   a : vraie ; b : vraie ; en d on définit la période temporelle
3. Propagation du son dans l'air :
   a- Il s'agit de la transmission de proche en proche de la vibration de couches d'air.
   b- Cette perturbation s'effectue parallèlement à la direction de propagation.
   c- La longueur d'onde d'un son périodique dépend de la fréquence.
   d- Dans un même milieu, un observateur entend les sons aigus plus rapidement que les sons graves issus simultanément de la même source.
   a : vraie ; b : vraie ; c : vraie ( la longueur d'onde dépend aussi du milieu) ; d : faux
4. La vitesse de propagation du son est de 333 m/s. Un avion volant à mach 1 vole " à la même vitesse que le son " ce qui correspond à 1000 km/h à l'altitude de l'avion. En utilisant ces données :
   a- La vitesse du son est indépendante de l'altitude.
   b- Une augmentation de température se traduit par une diminution de la vitesse du son.
   c- Il est impossible de voir arriver un avion qui franchit le mur du son.
   d- Le "bang" d'un avion volant à mach 1, à une altitude de 1 km est perçu environ 6 secondes après son passage à la verticale de l'observateur.
   a : fausse 1000 / 3,6 = 277 m/s ; b, c, d fausses.
5. On utilise les ultrasons émis à la fréquence de 40 kHz ; leur célérité dans les conditions de cette observation est 340 m/s.
   a- La distance parcourue pendant une période est 8,5 mm.
   b- La célérité est modifiée si on change la nature du gaz dans lequel ils se propagent.
   c- La fréquence est modifiée si on change la nature du gaz dans lequel ils se propagent.
   d- Si la fréquence des ultrasons est divisée par deux, alors leur vitesse de propagation dans un milieu donné est également divisée par deux.
   a : vraie ( 340/ 40000 = 8,5 mm ) ; b : vraie ; c, d : faux ;( d : la longueur d'onde double)
6. Un générateur de salves ultrasonores et deux récepteurs sont sur un même axe. Les récepteurs sont séparés d'une distance d. ces deux appareils sont reliès à un oscilloscope dont les règlages sont 0,1 ms/div et 50 mV/div. On obtient la figure 1. La célérité des ondes ultrasonores est 340 m/s.

   a- Le retard de l'onde reçue par l'un des récepteur par rapport à l'autre est environ 0,1 ms.
   b- Les deux récepteurs sont distants de d=20 cm.
   c- On déplace l'un des récepteurs, on obtient la figure 2. La nouvelle distance d' est supérieure à d.
   d- L'amplitude du signal reçu est 0,1 V.
   a : faux ; b : vrai d= 340 *6 10^-4 = 0,2 m vrai ; c : faux ( d' = 340*5 10^-4 = 0,17 m) ; d : vrai (2*0,05 V)

   
7. Une onde à la surface de l'eau est crée par une lame vibrant à la fréquence de 100 Hz. Sa célérité est 1 m/s.
   a- Après réflexion sur le bord de la cuve à onde, deux perturbations de sens opposé qui se croisent s'annihilent, c'est à dire qu'après le croisement , les perturbations ont disparu.
   b- Cette onde peut être diffracté par un ouverture de largeur 2 mmm.
   c- S'il y a diffraction, la forme de l'onde après l'ouverture est identique à la forme de l'onde avant l'ouverture.
   d- La longueur d'onde de l'onde incidente est identique à la longueur d'onde de l'onde diffractée.
   a : faux ; b : vrai (l= 1/100 = 0,01 m = 10 cm du même ordre que 2mm) vrai ; c:faux; d : vrai
8. Un haut parleur émet un son de fréquence f= 1000 Hz devant une fenètre de largeur a= 0,34 m. Le son émis diffracté par la fenètre ne parvient avec suffisamment d'amplitude ( et n'est donc pas audible) que si l'on se trouve dans la zone comprise entre les deux premières extinctions de part et d'autre de l'axe médian. Une personne est située en A. La célérité des ondes sonores est 340 m/s.

   a- Elle n'entend pas le son
   b- Elle n'entendra correctement que sur l'axe médian.
   c- Elle entend si la fréquence du son est doublée.
   d- Elle entend mieux les sons graves que les sons aigus
   (écart angulaire q=l/a avec l= 340 /1000 =0,34 m ; q= 1 rad = 57 ° supérieur à 45 ° position de A) a : faux ; b : faux si f double, alors l et donc q est divisée par deux c : faux ;
   sons graves basses fréquences donc l est plus grand ainsi que q : d : vrai

9. A propos de la lumière :
   a- La lumière est une onde transversale, dont la célérité est la même dans tout milieu transparent.
   b- La lumière blanche est constituée de plusieurs radiations qui ont la même longueur d'onde.
   c- La dispersion par un prisme est l'équivalent de la diffraction pour les ondes mécaniques progressives.
   d- La dispersion de la lumière blanche par un prisme montre que l'indice du milieu varie avec la fréquence.
   d : vrai
10. On éclaire une fente de largeur a avec une diode laser émettant une lumière rouge de longueur d'onde l= 650 nm ; on observe sur un écran placé à D= 1 m du fil une tache centrale de largeur L.
    a- L'écart angulaire du faisceau augmente si la largeur a utilisée augmente.
    b- L'écart angulaire du faisceau augmente si la distance de la fente à l'écran augmente.
    c- L'écart angulaire du faisceau augmente si la distance de la fente à la diode augmente.
    d- L'écart angulaire du faisceau diminue en utilisant un laser émettant une lumière bleue.
    écart angulaire q=l/a : d : vrai ( l _bleu voisine 450 nm)

    ---

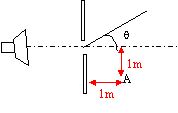
Une tige métallique MN de longueur L et de masse m est posée sur deux rails conducteurs parallèles séparés d'une distance D. La tige est perpendiculaire aux rails et glisse sans frottement sur les rails. La base des rails est alimentée par un générateur de courant continu stabilisé imposant une intensité I dans le circuit. Le plan où sont fixés les rails est incliné d'un angle a avec l'horizontale, les rails étant parallèles à la ligne de plus grande pente. Le montage est placé dans un champ magnétique uniforme et vertical de valeur B. L'étude se fait dans le référentiel terrestre.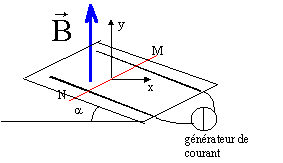

g= 10 m/s² ; L=20 cm ; m=100 g ; D= 10 cm; I= 10 A ; a =45° ; h=1,25 m ; l=1 m ; H=20 m

Partie I :

1. Indiquer le sens du courant dans la tige pour espérer réaliser l'équilibre de la barre sur les rails. Justifier.
2. Représenter le schéma en coupe de la barre dans le plan Oxy. Faire le bilan des forces s'appliquant à la barre et les représenter sur un schéma.
3. Pour quelle valeur de B la tige est-elle en équilibre sur les rails ?

Partie II :

Le champ magnétique est supprimé. La tige est lâchée sans vitesse initiale sur le plan incliné d'une hauteur h par rapport à la table, ensuite elle continue son trajet sur le plan horizontzl de longueur l. Les frottements sont négligés. Le rayon de la tige est suffisamment petit pour que le mouvement de la tige puisse être assimilé à un mouvement de translation dans le référentiel terrestre. Le mouvement de la tige est étudié dans le repère fixe O'xz.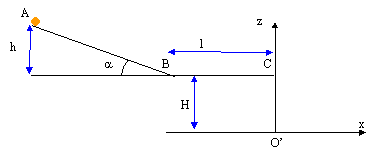

1. Déterminer qualitativement la nature du mouvement de G, centre de gravité de la tige entre A et B puis entre B et C.
2. Déterminer la vitesse de la tige en B.
3. Déterminer la vitesse de la tige en C.

Partie III : on étudie le mouvement de chute libre de la tige à partir de C avec v_C= 5 m/s.

1. Etablir les équations horaires du centre d'inertie de la tige.
2. En déduire l'équation de la trajectoire.
3. Soit d la distance horizontale entre l'impact de la tige sur le sol et la verticale du point C. Exprimer d en fonction de h et H. Calculer D.

---

corrigé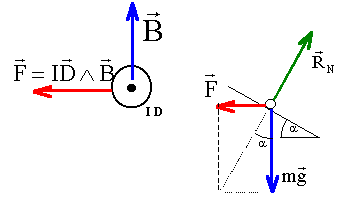

---

A l'équilibre tana = F/P= I D B / (mg)

soit B= mg tana / (ID) = 0,1*10*tan45 / (10*0,1)= 1 tesla.

---

entre A et B la tige est soumise à son poids P et à l'action normale R_N du support.

R_N perpendiculaire à la vitesse ne travaille pas

le poids effectue un travail moteur en descentede A à B : W_P= mg h l'énegie cinétique de la tige augmente ; donc la vitesse augmente ; G a un mouvement uniformément accéléré.

½mv_B² = mgh soit v_B= racine carrée (2gh) = (2*10*1,25)^½= 5 m/s.

entre B et C le poids et l'action du plan sont opposées : la tige est pseudo-isolée et le mouvement de G est rectiligne uniforme. v_C=5 m/s.

---

vecteur vitesse initiale ( v_C; 0) ; vecteur position initiale :( 0 ; H)

vecteur accélération : (0, -g )

le vecteur vitesse est une primitive du vecteur accélération : (v_C ; -gt)

le vecteur position est une primitive du vecteur vitesse :

x = v_Ct ; z= -½gt² + H

trajectoire : t = x / v_C ; d'où z = -½g x² / v_C² + H

au point d'impact I sur le sol : z=0 soit x_I² = 2 Hv_C² / g

or v_C² = 2gh ; x_I² = 4 Hh

d = racine carrée (4Hh) = (4*20*1,25)^½= 10 m.

---