Aurélie jan 04

Kiné Rennes d'après concours 2004

potassium-argon -lentilles - chute d'une bille - dihydrogène - chimie




Google



Les roches volcaniques contiennent du potassium dont un isotope, le potassium 40 est radioactif. Sa demi vie est t½=1,5 109 ans. Le noyau fils obtenu est l'argon 40 (gaz). Lors d'une éruption la lave au contact de l'air perd l'argon 40. Ce phénomène est appelé dégazage puisque juste après l'éruption, la lave ne contient plus d'argon 40.

  1. L'analyse d'un échantillon de roche de masse 1 kg montre qu'il contient mK=1,5 mg de potassium 40 et mAr= 0,0118 mg d'argon 40. Quelle est la date approximative de l'éruption dont est issu cet échantillon ? On considérera dans tout l'exercice que les atomes de potassium 40 et d'argon 40 ont la même masse.
  2. Pour déterminer l'âge des roches lunaires récupérées par les astronautes d'Apollo II on a évalué les quantités relatives de potassium 40 et d'argon 40 retenu dans la roche. Un échantillon de 1 g de roche contient V=82 10-4 mL d'argon 40 et m= 1,66 10-6 g de potassium 40. Le volume des gaz est mesuré dans les conditions normales de température et de pression. Estimer l'âge des roches lunaires.

masse molaire en g/mol : Ar=40 ; K=40 ; NA= 6,02 1023 mol-1 ; Vm=22,4 L/mol.

 

corrigé
au départ à t=0, N0 noyaux de potassium et aucun noyau d'argon.

nombre de noyaux de potassium 40 à la date t : NK=N0e-lt soit N0/ NK= elt

avec l= ln2 / t½ = 0,693 / 1,5 109 = 4,,62 10-10 an-1.

NK= mK/40 NA= 1,5 10-3 / 40 *6,02 1023 = 2,26 1019 noyaux

nombre de noyaux d'argon à la date t : NA=N0-NK

NA=mAr/40 NA= 0,0118 10-3 / 40 *6,02 1023 = 1,77 1017 noyaux

NA / NK =1,77 1017/ 2,26 1019 =7,8 10-3.

NA / NK = (N0-NK) / NK = N0/NK-1

N0/NK = NA / NK +1 = 7,8 10-3 +1 = 1,00783

1,00783 = elt ; ln 1,00783 = 4,62 10-10 t

t = 7,8 10-3 / 4,62 10-10 = 1,6 107 ans.

même méthode

NA=VAr/22,4 NA= 82 10-4 10-3 / 22,4 *6,02 1023 = 2,2 1017 noyaux

NK= mK/40 NA= 1,66 10-6 / 40 *6,02 1023 = 2,5 1016 noyaux

NA / NK = 2,2 1017/ 2,5 1016 = 8,8

N0/NK = NA / NK +1 = 8,8 +1 = 9,8

9,8 = elt ; ln 9,8 = 4,62 10-10 t

t = 2,28 / 4,62 10-10 = 4,94 109 ans.

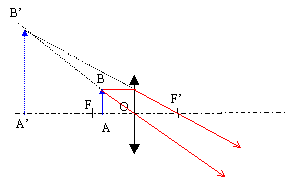
On considère un objet AB plan perpendiculaire à l'axe optique des instruments utilisés. A est sur l'axe optique. La taille AB= 0,5 cm. Soit une lentille convergente L1 de vergence C=50 d.

  1. Placer sur un schéma la lentille, ses foyers, le centre optique O1; on place AB à 1,5 cm à gauche de la lentille : construire l'image A'B'.
    - Déterminer graphiquement et par le calcul la taille et la position de l'image.
  2. On place l'objet AB à 5 cm à gauche de la lentille. Déterminer par le calcul la taille et la position de la nouvelle image A'1B'1.
corrigé
on écrit en bleu et en gras les mesures algébriques.

C=1/OA'-1/OA avec OA= -1,5 10-2 m ; C=50 d.

1/OA' =1/OA+C= -100/1,5 +50 = -16,66 soit OA' = -1/16,66 = -6 10-2 m = -6 cm.

grandissement : g=OA'/OA = A'B'/AB = -6/-1,5 = 4

taille de l'image virtuelle et droite : 4*0,5 = 2 cm.

C=1/OA'1-1/OA avec OA= -5 10-2 m ; C=50 d.

1/OA'1 =1/OA+C= -100/5 +50 = 30 soit OA'1 = 1/30= 3,33 10-2 m = 3,33 cm.

grandissement : g=OA'1/OA = A'1 B'1 /AB = 3,33/-5 = -0,66

taille de l'image réelle renversée par rapport à l'objet : 0,66*0,5 = 0,33 cm.

chutte d'une bille :

Une bille en acier de masse m et de diamètre d est abandonnée à t=0 sans vitesse initiale dans un tube vertical qui contient une solution de détergent pour vaisselle. A t=0 la bille est entierement immergée.

La force de frottement est de la forme f= 0,173 d²r0v².

d : diamètre de la bille ; r0 masse volumique de la solution de détergent ; v : vitesse du centre d'inertie de la bille.

L'équation différentielle relative à la vitesse du centre d'inertie de la bille est : dv/dt = 8,38-7,62 v²

  1. Déterminer la vitesse limite atteinte par la bille.
  2. Par la méthode d'Euler, déterminer la vitesse de la bille lorsque t=0,2 s. On prendra un pas Dt=0,04 s.
  3. Toujours en utilisant la méthode d'Euler, déterminer la date à laquelle on peut considérer que la bille atteint sa vitesse limite.
  4. Déterminer la masse de la bille.
  5. Déterminer le rayon de la bille.

g=9,81 m/s² et r0 =1000 kg/m3.

corrigé
vitesse limite atteinte par la bille : dv/dt =0 soit = 8,38-7,62 vlim²=0

vlim²=8,38 / 7,62 = 1,14 et vlim =1,067 m/s.

d'une part Dv/Dt= a soit vn+1-vn= a Dt (1) avec Dt = 0,04 s

d'autre part a=Dv/Dt= 8,38-7,62 v² (2)

v0= 0 m/s ; (2) donne a0 = 8,38 m/s²

t= 0,04 s : (1) donne v1 = v0 + a0Dt = 0 + 8,38*0,04 =0,335 m/s

t= 0,08 s : a1 = 8,38-7,62 v²1 =8,38-7,62*0,335² = 7,52 m/s²

v2 = v1 + a1Dt = 0,335 + 7,52*0,04 = 0,636 m/s.

t= 0,12 s : a2 = 8,38-7,62 v²2 =8,38-7,62*0,636² = 5,3 m/s²

v3 = v2 + a2Dt = 0,636 + 5,3*0,04 = 0,848 m/s.

t= 0,16 s : a3 = 8,38-7,62 v²3 =8,38-7,62*0,848² = 2,9 m/s²

v4 = v3 + a3Dt = 0,848 + 2,9*0,04 = 0,946 m/s.

t= 0,2 s : a4 = 8,38-7,62 v²4 =8,38-7,62*0,946² = 1,3 m/s²

v5 = v4 + a4Dt = 0,946 + 1,3*0,04 = 0,998 m/s.

t= 0,24 s : a5 = 8,38-7,62 v²5 =8,38-7,62*0,998² = 0,791 m/s²

v6 = v5 + a5Dt = 0,998 + 0,791*0,04 = 1,03 m/s.

t= 0,28 s : a6 = 8,38-7,62 v²6 =8,38-7,62*1,03² = 0,3 m/s²

v7 = v6 + a6Dt = 1,03 + 0,3*0,04 = 1,042 m/s.

t= 0,32s : a7 = 8,38-7,62 v²7 =8,38-7,62*1,042² = 0,105 m/s²

v8 = v7 + a7Dt = 1,042 + 0,105*0,04 = 1,046 m/s.

t= 0,36s : a8 = 8,38-7,62 v²8 =8,38-7,62*1,046² = 0,039 m/s²

v9 = v8 + a8Dt = 1,046 + 0,039*0,04 = 1,0475 m/s.

à t = 0,4 s la vitesse limite est atteinte.

masse de la bille :

la bille est soumise à son poids, vertical vers le bas , valeur mg=rmétal Vbille g

à la poussée d'Archimède, verticale vers le haut, valeur r0 Vbille g

à la force de frottement verticale, vers le haut : f= 0,173 d²r0v².

la seconde loi de Newton s'écrit suivant un axe vertical orienté vers le bas :

m g-r0 Vbille g -0,173 d²r0v²= mdv/dt

g ( 1-r0 Vbille /m) -0,173 d²r0 / m v²= dv/dt

g ( 1-r0 /rmétal) -0,173 d²r0 / m v²= dv/dt

identifier à : 8,38-7,62 v² = dv/dt

8,38 = 9,81 ( 1-1000 /rmétal) ; 1-1000 /rmétal=8,38/9,81=0,855

1-0,855 = 1000 /rmétal ; rmétal= 1000 / 0,145= 6900 kg/m3.

d'autre part : 0,173 d²r0 / m = 7,62 avec m = rmétal 4/3 pr3et d²= 4 r² et r0 =1000

173 *3/ (6900*3,14 r) = 7,62 ; r = 173*3/(6900*3,14*7,62)=3,14 10-3 m = 3,14 mm.

volume de la bille : 4/3*3,14*(3,14 10-3 )3=1,3 10-7 m3

masse de la bille : 6900*1,3 10-7 =9 10-4 kg.

préparation du dihydrogène

 On effectue l'électrolyse de l'eau acidifiée pour préparer le dihydrogène. On travaille sous une tension U=1,85 V et avec une intensité I= 10 kA. L'équation de la transformation qui se produit s'écrit : 2H2O(l)= 2H2(g) + O2(g)

  1. A quelle électrode se dégage le dihydrogène ?
    - A quelle pôle du générateur est-elle branchée ?
    - Ecrire l'équation de la réaction d'électrode correspondante.
  2. Quel est le volume de dihydrogène obtenu en 1 heure ? ( Vm = 24 L/mol)
  3. Calculer l'énergie électrique consommée pour produire 1 m3 de dihydrogène.
corrigé
le dihydrogène se dégage à la cathode négative, reliée à la borne moins du générateur

l'ion H+ est réduit : 2H+ + 2e- = H2(g)

ou 2H3O+ + 2e- = H2(g)+ 2H2O(l)

Qté d'électricité : Q= I t = 104*3600 =3,6 107 C

Qté de matière d'électrons : 3,6 107 /96500 =373 mol

Qté de matière dihydrogène : 0,5*373 =186,5 mol

volume dihydrogène : 186,5*24 = 4,47 103 L = 4,47 m3.

énergie consommée en une heure : U I t = U Q = 1,85 *3,6 107 = 6,66 107 J

énergie consommée par m3 de gaz produit :6,66 107 /4,47 =1,49 107 J.


Solubilité de l'acide benzoïque

On réalise à 20 °C une solution d'acide benzoïque en introduisant une masse m=1,22 g d'acide benzoïque dans un volume V= 100 mL d'eau distillée. Le pH de la solution obtenue vaut environ 3. La solubilité de l'acide benzoïque est 2,4 g/L à 20°C. Masse molaire acide benzoïque : 122 g/mol.

  1. Montrer que la solution est saturée.
  2. L'équation de la réaction de l'acide benzoïque avec l'eau s'écrit :
    C6H5-COOH + H2O= C6H5-COO- + H3O+.(1)
    On fait trois proposition afin de dissoudre la totalité de l'acide benzoïque dans l'eau :
    a- Ajouter de l'eau distillée.
    b- Ajouter quelques gouttes d'acide nitrique.
    c- Ajouter quelques gouttes d'une solution concentrée d'hydroxyde de sodium
    Approuver ou réfuter chaque proposition en justifiant.
  3. Suite à l'une des trois opérations la solution a un pH=5. par ailleurs à pH=5 la composition centésimale est la suivante :
    acide benzoïque 14% et ion benzoate : 86 %. En déduire la constante d'acidité ka associée à la réaction (1).

 

corrigé
1,22 g dans 0,1 L correspond à 12,2 g /L valeur bien supérieure à la solubilité ( 2,4 g/L)

la solution est donc saturée

en ajoutant suffisamment d'eau ( environ 0,4 L) on va dissoudre tout le solide : 1,22 / (0,1+0,4) =2,44 g/L

en ajoutant des ions hydroxyde HO-, on déplace l'équilibre (1) vers la formation d'ion benzoate qui lui est soluble dans l'eau.

On va dissoudre tout le solide.

par contre en ajoutant de l'acide nitrique on déplace l'équilibre (1) vers la formation d'acide benzoïque et le solide ne se dissout pas.

Ka = [C6H5-COO-][H3O+]/[C6H5-COOH] avec [C6H5-COO-]=[H3O+] =10-5 mol/L

[C6H5-COOH] = 14 / 86[C6H5-COO-] = 1,63 10-6 mol/L

Ka =10-5 *10-5 / 1,63 10-6 = 6,1 10-5.

Détermination du degré alcoolique d'une boisson.

On prèlève 10 mL d'un vin blanc auquel on ajoute de l'eau et on distille ce mélange. Le distillat contient l'alcool du vin. On verse ce distillat dans une fiole jaugée de 100 mL et on complète avec de l'eau distillée jusqu'au trait de jauge. Soit S1 la solution obtenue. Dans un bécher on introduit 10 mL de la solution S1, 20 mL de solution de dichromate de potassium K2Cr2O7 à 0,1 mol/L et environ 20 mL d'acide sulfurique à 2 mol/L. On obtient la solution S2. Sa couleur orangée demeure. On ajoute alors une solution de sulfate de fer II à 0,5 mol/L. Le volume nécessaire pour que le mélange vire au vert est 8,9 mL.

Quelle est la concentration de l'alcool dans l'échantillon de vin blanc ?

couples redox : Cr2O72-/Cr3+ ; Fe3+ / Fe2+ ; CH3COOH / CH3CH2OH

corrigé
oxydation de l'éthanol par l'ion dichromate :

CH3CH2OH + H2O = CH3COOH + 4H+ + 4e-.

Cr2O72-+ 14H++6e- = 2Cr3+ + 7H2O

3 CH3CH2OH + 2Cr2O72-+ 16H+= 3CH3COOH + 4Cr3+ + 11H2O (1)

oxydation de l'ion fer II par l'ion dichromate en excès :

Fe2+ = Fe3++e-.

Cr2O72-+ 14H++6e- = 2Cr3+ + 7H2O

6 Fe2+ + Cr2O72-+ 14H+ = 6Fe3++ 2Cr3+ + 7H2O (2)

Qté de matière d'ion Fe(II ): 0,5 * 8,9 10-3 = 4,45 10-3 mol

Qté de matière d'ion dichromate en excès : 4,45 10-3 /6 = 7,42 10-4 mol

Qté initiale de dichromate de potassium : 0,1*20 10-3 = 2 10-3 mol

Qté d'ion dichromate ayant oxydé l'alcool : 2 10-3 -7,42 10-4 =1,258 10-3 mol

Qté de matière d'alcool dans 10 mL de S1: 1,5*1,258 10-3 =1,89 10-3 mol

Qté de matière d'alcool dans le distillat :10*1,89 10-3 =1,89 10-2 mol

Qté de matière d'alcool dans 10 mL de vin blanc :1,89 10-2 mol

concentration de l'alcool : 1,89 10-2 /0,01 = 1,89 mol/L.

pourcentage de cuivre et d'argent dans un alliage .

Un alliage de cuivre et d'argent de masse m= 6,54 g est chauffé avec de l'acide sulfurique concnetré. Il se produit les réactions d'équations :

2H2SO4 + Cu = Cu2+ + SO42- + SO2(g) + 2H2O.

2H2SO4 + 2Ag = 2Ag+ + SO42- + SO2(g) + 2H2O.

Après refroidissement on mesure le volume de gaz à 25°C sous une pression p=1,02 105 Pa: il vaut 1,43 L

Calculer les pourcentage massique de cuivre et d'argent contenus dans cet alliage.

masse molaire en g/mol : Ag= 107,9 ; Cu= 63,5. R= 8,31 Jmol-1 K-1.

corrigé
soit mCu la masse de cuivre et mAg la masse d'argent : mCu + mAg =6,54.

Qté de matière de cuivre nCu = mCu / 63,5 ; Qté de matière d'argent : nAg = mAg / 107,9

63,5 nCu + 107,9 nAg =6,54 (1)

Qté de matière de dioxyde de soufre : nCu +½nAg =1,43 / Vm.

calcul du volume molaire : Vm = RT/p= 8,31*(273+25)/1,02 105=24,28 L

nCu +½nAg =1,43 / 24,28 = 5,89 10-2.(2)

d'où nCu = 5,89 10-2-½nAg

repport dans (1) : 63,5 (5,89 10-2-½nAg )+ 107,9 nAg =6,54

3,74 -31,75 nAg + 107,9 nAg =6,54

nAg =(6,54-3,74)/ (107,9-31,75)=2,8 /76,15 =3,68 10-2 mol

d'où nCu = 5,89 10-2-0,5*3,68 10-2= 4,05 10-2 mol

mCu = 63,5*4,05 10-2 = 2,57 g ; mAg = 107,9*3,68 10-2 = 3,97 g ;

% massique en cuivre : 257/6,54 = 39,3 % ; % massique en argent : 397/6,54 =60,7 %.

retour -menu