Aurélie jan 04

Manipulateur radio d'après concours 2004 (Rennes)

mécanique -datation au carbone 14- l'aspirine




Google



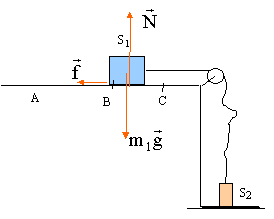
On entraîne un solide S1 de masse m1 par la chute d'un solide S2 de masse m2 sur une hauteur H. Ainsi lancé sur la longueur H, le solide S1 frottant sur le support horizontal parcourt la distance d avant de s'arrèter. Le fil de liaison est supposé inextensible et de masse négligeable. On néglie la masse de la poulie de transmission. On note f la valeur de la force de frottement qui est constante tout le long du parcourt AC. La vitesse initiale en A est nulle.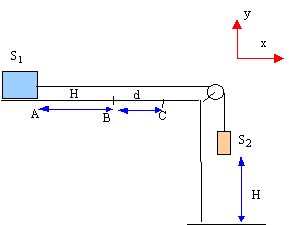

étude dynamique sur le parcourt AB :

  1. Faire le bilan des forces appliquées sur les solides sur le parcours AB.
  2. Appliquer la deuxième loi de Newton aux deus solides
    - Projeter ces relations sur les axes Ox et Oy et déterminer l'expression de l'accélération "a" du solide S1 en fonction de m1, m2, g et f.
  3. La mesure de l'accélération du mobile sur ce parcourt est a= 3 m/s². Calculer la valeur de la force de frottement f.
  4. Le temps pour réaliser ce parcours AB est 0,5 s. Calculer la vitesse au point B et déterminer H.

étude dynamique sur le parcourt AB :

  1. Faire le bilan des forces appliquées au solide S1 durant ce parcours.
  2. La vitesse en B est vB=1,5 m/s. Déterminer la distance d.

m1 = 1,4 kg ; m2 = 850 g ; g= 9,8 m/s².

corrigé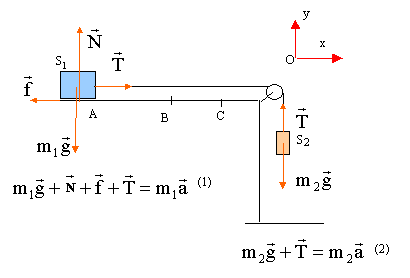

(1) s'écrit sur l'axe Ox : -f + T=m1a

(2) s'écrit sur l'axe Ox : -m2g + T=- m2a

éliminer la tension T : -m2g +m1a +f = -m2a

a = (m2g -f) / (m1+m2).

f = m2g- a (m1+m2) = 0,85*9,8- 3*(1,4+0,85) =8,33 -6,75 = 1,6 N.

le mouvement de S1 est rectiligne uniformément accéléré, sans vitesse initiale

Les origines des espaces et des dates sont prises au départ en A.

v(t) = a t ; x(t) = ½at² ; v²B = 2aH

vB= 3*0,5 = 1,5 m/s ; H= v²B /( 2a) = 1,5²/6= 0,375 m.

sur le parcours BC seule la force de frottement travaille ( poids et action normale du support sont perpendiculaires à la vitesse)

W(f) = f d cos (180 ) = -fd

variation de l'énergie cinétique entre B et C : DEc= 0-½m1v²B.

théorème de l'énergie cinétique : -fd = -½m1v²B.

d= ½m1v²B / f = 0,5*1,4*1,5²/ 7 = 0,225 m.

"Le carbone 14 est produit dans la haute atmosphère où les protons du rayonnement cosmique percutent les molécules qui composent l'air. Les réactions nucléaires qui résultent de ces chocs produisent des neutrons secondaires. Ces neutrons ont une forte probabilité de réagir avec l'azote de l'air ( 14N) pour donner un proton et un isotope du carbone : le carbone 14. dans le milieu naturel la production du carbone 14 et sa disparition par désintégration radioactive s'équilibrent. On estime qu'il y a environ 10-12 fois moins d'atomes de carbone 14 que d'atomes de carbone stable (12 C). Il en résulte une radioactivité faible du carbone.... Lors de la mort de l'organisme cet équilibre est rompu. Les atomes de carbone 14 disparaissent peu à peu."

Données : numéro atomique C : Z=6 ; N: Z=7.

La demi vie du carbone 14 est T=5730 ans ; lors de la désintégration du carbone 14 on détecte des particules b-.

masse atomique molaire C=12 g/mol

NA= 6,02 1023 mol-1.

A partir du texte répondre aux questions :

  1. Donner la composition des noyaux des deux isotopes du carbone ainsi que celui de l'azote.
  2. Ecrire la réaction nucléaire qui produit le carbone 14 dans l'atmosphère.
  3. Après avoir défini l'activité A d'un échantillon, déterminer l'activité d'un échantillon contenant 1 g de carbone lorsqu'il se trouve à l'équilibre.
  4. Définir la particule b-. Ecrire la réaction nucléaire de désintégration du carbone 14.
  5. Donner la loi de décroissance radioactive des noyaux de carbone 14.
  6. Dans la grotte de Chauvet (Ardèche) on a récupéré des fragments de charbon de bois qui avaient permis de réaliser les gravures pariétales. Le nombre Nch d'atomes de carbone 14 dans 2 g de charbon a donné Nch= 2,1 109 atomes. Calculer l'âge attribué à ces gravures.
corrigé

carbone 12 : 6 protons et 6 neutrons ; carbone 14 : 6 protons et 8 neutrons ; azote 14 : 7 protons et 7 neutrons

147N + 10n --> 146C + 11p

146C -->AZX + 0-1e ( électron)

activité A: nombre de désintégrations par seconde ; elle s'exprime en becquerel (Bq)

A= l N

dans 1 g de carbone il y a : 1/12*6,02 1023 = 5 1022 atomes de carbone

soit environ N= 5 1022 * 10-12 = 5 1010 atomes de carbone 14.

l T½=ln2 avec T½ = 5730 ans = 5730*365*24*3600 = 1,8 1011 s

l = ln2 / 1,8 1011 = 3,85 10-12 s-1.

activité A = 3,85 10-12 * 5 1010 = 0,2 Bq.

loi de décroissance radioactive : NCh = N0 e -lt ou ln(N0 /NCh)= lt

dans 2 g de charbon Nch= 2,1 109 atomes donc dans 1 g : Nch= 1,05 109 atomes 14C.

N0 = 5 1010 atomes de carbone 14 dans 1 g ; l = ln2 / 5730 = 1,21 10-4 an-1.

ln(N0 /NCh)= ln(5/0,105 )= 3,86

t = 3,86 / 1,21 10-4 = 3,2 104 ans.

 On prépare V1= 10 mL d'une solution aqueuse S1 d'acide éthanoïque de concentration C1 = 0,2 mol/L. On ajoute rapidement à cette solution V2 = 15 mL d'une solution aqueuse S2 d'hydrogénocarbonate de sodium ( Na+ + HCO3-) de concentration c2 = 0,1 mol/L. On suppose que les réactions de l'acide éthanoïque et de l'ion hydrogénocarbonate avec l'eau est négligeable. l'acide éthanoïque appartient au couple CH3COOH / CH3COO- de pka1 = 4,8 ; l'ion hydrogénocarbonate est la base conjuguée du couple acide base H2O, CO2 dissous / HCO3- de pKa2 = 6,4

  1. Ecrire l'équation de la réaction acido-basique susceptible de se produire lors du mélange des solutions S1 et S2 et calculer la constante d'équilibre associée K.
  2. Exprimer puis calculer le quotient de réaction initial Qr i. En déduire le sens d'évolution spontané du système chimique.
  3. Dresser le tableau d'avancement du système chimique et calculer la valeur de l'avancement à l'équilibre xéq.
    - Calculer le taux d'avancement final. La réaction est-elle totale ?
    - Calculer les concentrations des espèces chimiques présentes en solution à l'état final.
  4. La solubilité du dioxyde de carbone dans les conditions de l'expérience est 0,04 mol/L. Qu'observe-t-on ? Le système chimique évolue-t-il ? Justifier.
    corrigé
    CH3COOH + HCO3- = CH3COO- + H2O+ CO2
K= [CH3COO- ]éq[ CO2 dissous]éq / ( [CH3COOH ]éq[HCO3-]éq )

avec Ka1 = [CH3COO- ]éq[H3O+] / [CH3COOH ]éq

et Ka2 = [HCO3- ]éq[H3O+] / [ CO2 dissous]éq

K= Ka1 /Ka2 = 10-4,8 / 10-6,2 = 101,4= 25,1.

quotient de réaction initial Qr i= [CH3COO- ]i[ CO2 dissous]i / ( [CH3COOH ]i[HCO3-]i ) =0

Qr i < K donc évolution spontanée dans le sens directe ( gauche à droite).

avancement
CH3COOH
+ HCO3-
= CH3COO-
+ CO2
+ H2O
initial
0
0,2*0,01

= 2 10-3 mol
0,1*0,015

=1,5 10-3 mol
0
0
solvant
en cours
x
2 10-3 -x
1,5 10-3 -x
x
x
fin
xéq
2 10-3 -xéq
1,5 10-3 -xéq
xéq
xéq

xmax =

1,5 10-3 mol
2 10-3 -xmax
1,5 10-3 -xmax

fin
1,38 10-3 mol.
0,62 10-3 mol.
0,12 10-3 mol.
1,38 10-3 mol.
1,38 10-3 mol
K= 25,1 = x2éq / ((2 10-3 -xéq)(1,5 10-3 -xéq))

25,1(2 10-3 -xéq)(1,5 10-3 -xéq) = x2éq .

24,1 x2éq - 8,785 10-2 xéq+ 7,53 10-5 = 0

D= (8,785 10-2)²-4*24,1*7,53 10-5 =4,58 10-4 ; racine carrée ( )= 0,0214.

xéq = ( 0,0878 -0,0214) / (2*24,1) = 1,38 10-3 mol.

taux d'avancement final t = xéq / xmax = 1,38 /1,5 = 0,92 réaction partielle.

[Na+]fin = 0,1 *15 / (10+15) = 0,06 mol/L

[CH3COO- ]éq = [ CO2 dissous]éq = 1,38 10-3 / 25 10-3 = 0,0552 mol/L

[CH3COOH ]éq= 0,62 10-3 / 25 10-3 = 0,0248 mol/L

[HCO3-]éq =0,12 10-3 / 25 10-3 = 0,0048 mol/L

[ CO2 dissous]éq supérieure à la solubilité du dioxyde de carbone ; donc une partie du gaz se dégage

une partie du CO2 se dégage : tout ce passe comme si l'un des produits était partiellement éliminé et l'équilibre est donc déplacé vers la droite, dans le sens direct.

retour -menu