|
ondes(8 points) -expérience de Millikan (12 points)- l'aspirine ( 5points)- pile
zinc argent (5 points)
|
||||||
|
||||||
|
|
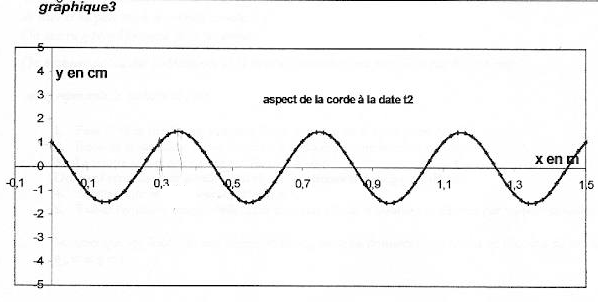
On considère une corde horizontale de longueur L= 1,5 m. On impose à l'extrémité S d'abscisse x=0 de la corde un mouvement vertical sinusoïdal de fréquence f et d'amplitude a. L'équation horaire du mouvement de S est notée yS(t). A l'instant t=0 le point S passe en montant au point d'ordonnée 0. Des ondes périodiques progressives se propagent le long de la corde à la célérité v. Le graphique 1 donne la représentation graphique de yS(t) ainsi que la représentation graphique de yM(t) équation horaire d'un point M de la corde d'abscisse xM. 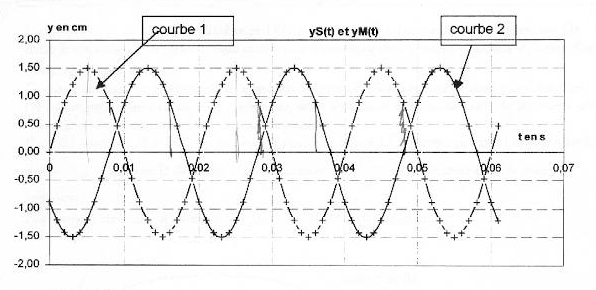 Les graphiques 2 et 3 donnent les représentations de la corde à deux dates différentes t1 et t2. Les échelles sont différentes dans les directions horizontale et vertical pour plus de clarté. 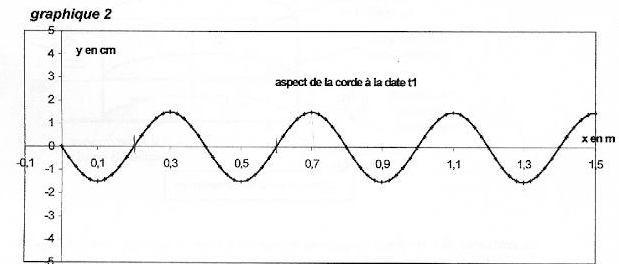
Indiquer la ou les bonnes réponses en justifiant rapidement à l'aide de données, lois, théorèmes définitions ou propriètés. Les réponses non justifiées ne seront pas prises en compte.
corrigé La courbe 1 représente yS(t) : à l'instant t=0 le point S passe en montant au point d'ordonnée 0. L'amplitude du mouvement de S est Ym=1,5 cm : valeur lue entre y(t)=0 et la valeur maximale de y(t). La période du mouvement de S est T=0,02 s = 20 ms La longueur d'onde est l=0,4 m = 40 cm ( lecture entre deux maximum sur le graphe 2) L'onde est une onde transversale ( déformation perpendiculaire à la direction de propagation), progressive, progressive périodique La célérité de l'onde est v= l T= 0,4/0,02 = 20 m/s. Le retard horaire du mouvement de M sur celui de la source est q=8 ms ( lecture entre le premier maxi courbe1 et le premier maxi courbe 2 sur le graphe 1) L'abscisse du point M peut avoir comme
valeur xM= vq = 20*8 10-3 = 0,16 m = 16 cm = 160 mm. La corde a été représentée sur la figure 3 à la date t2 qui peut être : 8 ms + un nombre entier de période ( 28 ms) Si on double la fréquence du signal la longueur d'onde est divisée par 2 (l = v/ n avec v constante) La célérité d'une onde le long d'une corde est proportionnelle à la racine carrée de la tension de la corde .Si on double la tension de la corde sans changer la fréquence du signal, la longueur d'onde est alors multipliée par 1,4 ( racine carrée de 2)
|
|||||
|
On étudie le mouvement d'une goutte d'huile chargée électriquement en chute verticale et soumise à l'action d'un champ électrique E constant. Ce champ est produit entre les armatures horizontales d'un condensateur plan, placé dans l'air. On admet que ce champ est uniforme entre les armatures, il est orienté de la plaque positive A vers la plaque négative B. Entre les armatures A et B du condensateur il existe une tension UAB positive ou nulle. On peut relier la tension UAB à la valeur du champ E par la relation E= UAB /d avec d la distance des armatures. Une charge subit dans ce champ E une force colinéaire au vecteur E ; F=qE. ( les vecteurs sont écrits en gras et en bleu) 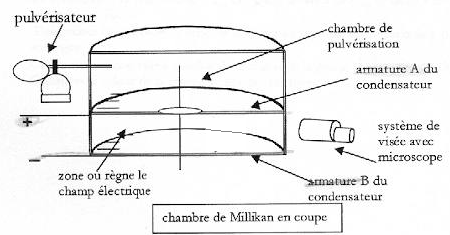 Une goutte d'huile sphérique de rayon r, de masse m, de charge q, tombe entre les armatures du condensateur. On observe la chute de la goutte dans la zone entre les armatures A et B à l'aide d'un système de visée et on peut ainsi obtenir sa vitesse v. On pose g l'intensité de la pesanteur. On néglige la poussée d'Archimède et la force de frottement est modélisée par f= -6prhv où h représente la viscosité de l'air.
corrigé 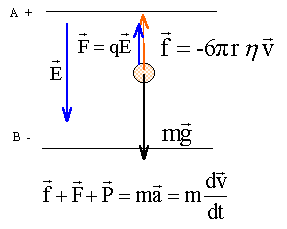
la charge q portée par la goutte est négative ( électrons) La somme vectorielle des forces appliquées à la goutte est égale au produit de la masse de la goutte par l'accélération de son centre d'inertie. Toutes les forces sont verticales et de plus le vecteur vitesse initiale est nulle : en conséquence le mouvement s'effectue sur la verticale. projection de la deuxième loi de Newton sur un axe vertical orienté vers le bas -6prhv -|q|uAB/d +mg = ma à t=0 la force de frotement est nulle ( car la vitesse initiale est nulle) donc l'accélération initiale vaut : g-|q|uAB/(md ) équation différentielle relative à la vitesse v(t) : -6prhv -|q|uAB/d +mg = mdv/dt dv/dt +6prh / m v = g-|q|uAB/(md ) (1) lorsque la vitesse limite est atteinte ( mouvement rectiligne uniforme dv/dt=0) 6prh / m vlim = g-|q|uAB/(md ) vlim =[mg-|q|uAB/d] / (6prh ) v(t) = vlim( 1- e-t/t) ; dv/dt = vlim/t e-t/t. repport dans l'équation différentielle (1) vlim/t e-t/t + 6prh / m vlim-6prh / m vlim e-t/t = g-|q|uAB/(md ) vlim e-t/t [1/t-6prh / m] + 6prh / m vlim= g-|q|uAB/(md ) expression de t : 1/t-6prh / m =0 ; t = m / (6prh ). v = vlim( 1- e-t/t) ; v / vlim= 1- e-t/t ; 1- v / vlim=e-t/t ; (vlim-v) / vlim=e-t/t ; |(v-vlim)/v| = e-t/t ; 0,01<= e-t1/t ln 10-2 <= -t1/t ; 4,6 <=-t1/t ; t1>= 4,6 t ; t1>= 4,6 m / (6prh ). rayon de la goutte r : masse (kg) = volume (m3) fois masse volumique (kg m3) m = 4/3pr3r ; or vlim =[mg-|q|uAB/d] / (6prh ) ; si la tension uAB est nulle : vlim =mg / (6prh ) vlim = 4/3pr3r g / (6prh ) ; vlim = 2r2r g / (9h ) r2 = 9h vlim / (2r g). r =[9*18 10-6 * 4 10-5 / ( 2*800*10)]½ =6,3 10-7 m la goutte est immobile sous l'action de son poids et de la force électrique de Coulomb; ces deux forces sont opposées et ont la même valeur |q|uAB/d =mg ; |q|= mgd /uAB = 4/3pr3r gd/ uAB . |q| vaut 3 fois la charge élémentaire e = 1,6 10-19 C la goutte est chargée de 3 électrons.
|
||||||
|
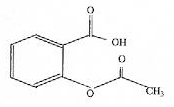
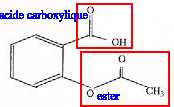
saponification de la fonction ester : solution de soude concentrée, chauffage à reflux durant 30 min. CH3-COO-C6H4-COO- : base conjuguée AH + H2O= A- + H3O+. Qr éq=[A-][H3O+]/[AH ] = 10-3,5. cette valeur est très faible, la réaction de l'aspirine avec l'eau est très limitée. Dans l'estomac le pH est très inférieur au pka du couple acide base : la forma qcide AH prédomine. Dans l'intestin, le pH est supérieur au
pka du couple acide base : la forme base conjuguée prédomine.
on utilise l'acide éthanoïque (ou acétique) par contre, en utilisant l'anhydride
acétique ( ou éthanoïque) CH3-CO-O-CO-CH3 , la
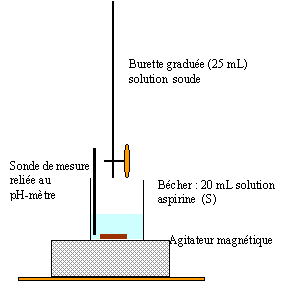
réaction sera rapide et totale. AH+ HO- --> A-+H2O à l'équivalence on a une solution acéthylsalycilate de sodium contenant la base A- : le pH sera donc supérieur à 7. 0 l'équivalence les quantités de matière d'acide et de soude sont en proportions stoéchiomètriques. 20 Ca = 7,7 *0,05 soit Ca = 7,7*0,05/20 = 1,925 10-2 mol/L or la fiole jaugée ne contient que 0,1 L, donc 1,925 10-3 mol d'aspirine issu du comprimé. masse d'aspirine dans un comprimé : 180*1,925 10-3 = 0,346 g = 346 mg l'écart avec l'indication de l'étiquette est inférieure à 1%.
|
||||||
|
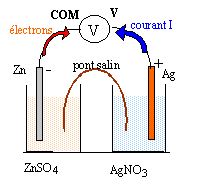
Un élève veut réaliser une pile zinc argent et dispose pour cela d'une lame d'argent, d'une lame de zinc, d'un bécher contenant un volume V1 = 100 mL de solution aqueuse de nitrate d'argent de concentration initiale en ion argent C1 = 0,2 mol/L, d'un bécher contenant un volume V2= 100 mL de solution de sulfate de zinc de concentration initiale en ion zinc C2 = 0,1 mol/L, d'un pont ionique au nitrate de potassium saturé. Le volume de chaque lame métallique est 10 mL. Pour vérifier son fonctionnement il dispose d'un voltmètre,
d'un ampèremètre d'un conducteur ohmique de résistance R et d'un
interrupteur. Constante d'équilibre de la réaction entre le zinc métal et les ions argent : K= 1052. Masse molaire atomique (g/mol) : Ag : 107,9 ; Zn : 65,4. masse volumique (g/mL) mAg= 7,1 : m Zn = 10,3. A sens d'évolution spontané du système :
B Pile en fonctionnement : L'élève réalise la pile et branche un voltmètre aux bornes de celle-ci.
corrigé Zn(s) + 2Ag+ = Zn2+ + 2Ag(s) Qr i =[ Zn2+] /[Ag+]²= 0,1/0,2²= 2,5 valeur inférieure à K, donc évolution dans le sens direct. à l'anode négative, le zinc s'oxyde : Zn(s) = Zn2+ + 2e-. à la cathode positive, les ions argent se réduisent : 2Ag+ + 2e- = 2 Ag(s) - Zn / Zn2+ // Ag+ / Ag +
en solution : les ions Zn2+ migrent vers le zinc métal ; les ions sulfates négatifs migrent en sens contraire les ions argent positif s'éloignent de l'argent métal; les ions nitrates négatif migrent en sens contraire. dans le pont salin : la demi pile de droite s'appauvrit en ion Ag+ : pour conserver l'électroneutralité de la solution les ions K+ du pont salin y migrent. la demi pile de gauche gagne des ions Zn2+
: pour conserver l'électroneutralité de la solution les ions NO3-
du pont salin y migrent.
Or la charge d'une mole d'électrons vaut en valeur absolue 96500 C Qté de matière d'électrons :0,965 * 5*60 / 96500 = 3 mmol Zn(s) = Zn2+ + 2e-. Qté de matière de zinc disparu : 1,5 mmol soit en masse 65,4*1,5 10-3 = 0,098 g initialement 10*10,3 = 103 g de zinc masse finale de zinc :103-0,098 = 102,9 g. Qté de matière d'ion zinc apparu : 1,5 mmol initialement on avait 100*0,1 = 10 mmol d'ion zinc au total 11,5 mmol ion zinc dans 100 mL : [Zn2+]=11,5/100 = 0,115 mol/L. Ag+ + e- = Ag(s) Qté de matière d'agent formé : 3 mmol soit en masse 107,9*3 10-3 = 0,32 g initialement 10*7,1 = 71 g d'argent masse finale d'argent : 71,32 g. Qté de matière d'ion agrent disparu : 3 mmol initialement on avait 100*0,2 = 20 mmol d'ion argent au final 17 mmol d'ion argent dans 100 mL : [Zn2+]=17/100 = 0,17 mol/L. |
||||||
|
|