|
gravitation -radioactivité - dipôle LC - chute d'une bille - diffraction - solution d'ammoniac préparation du dihydrogène - solubilité
du chlorure d'argent
|
||||||
|
||||||
|
|
On considère 2 corps sphériques A et B, de centre GA et GB, de rayon r, de masse m et de masse volumique µ. Ils sont au contact l'un de l'autre. On appelle G la constante de gravitation universelle. 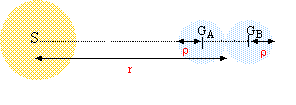 Données et approximations utiles : le volume d'une sphère de rayon R est V = 4/3 p R3; 1 / (r - r )² - 1 / (r + r )² =approximativement 4r / r3 1,33 = approximativement 2,2 = approximativement 1,5²
Si µ = 1000 kg.m-3, calculer r0 en km. Si r0 = 1000 000 km, calculer µ. corrigé intensité des forces gravitationnelles entre ces deux corps : forces attractives dirigées suivant GAGB de même valeur : F= Gm²/(2r)²= Gm²/ (4r²) force attractive exercée par saturne sur A: FA= GMm/(r-r)² force attractive exercée par saturne sur B: FB= GMm/(r+r)² différence de ces deux valeurd : FAB= GMm( 1/(r-r)² - 1/ (r+r)²)= GMm 4r/r3. les deux corps tendent à se séparer si FAB devient supérieure à F. à la limite de la séparation : GMm 4r/r03=Gm²/ (4r²) M 4r/r03=m/ (4r²) soit r03=16Mr3/m avec m= 4/3pr3m d'où : r03=12M/p *1/m. r0=(12M/p )1/3*1/m1/3= 1,3 109 /m1/3. m intervient au dénominateur : r0 sera dautant plus grand que les matériaux seront moins denses. Les plus légers seront donc à une distance plus grande de saturne alors que les plus denses sront plus proches. si m = 1000, alors m1/3=10 et r0= 1,3 109/10 = 1,3 108 m = 1,3 105 km. si r0= 109 m alors m1/3=1,3 109 / 109 = 1,3 et m= 2,2 kg/m3.
|
|||||
|
Quand on envoie des deutons- ou noyaux de deutérium 21H sur une substance contenant du sodium 23, il y a formation de sodium 24 et d'une autre particule X. Pendant un intervalle de temps D T très bref, le rapport entre le nombre de noyaux de sodium 24 formés et D T est constant et vaut Q. Données : 10Ne ; 11Na ; 12Mg Demi-vie du sodium 24 : t ½ = 14h ln 2 = 0,7 ; Q = 108 s-1 ; e-1 = 0,37
corrigé 2 21H+ 1123Na-->1124Na + AZX conservation de la charge électrique: 2+11=11+z soit Z=2 conservation du nombre de nucléons : 4+23=24+A soit A=3 donc AZX est 32He 1124Na --> 1224Mg + -10e formation de 1124Na : DN1 = QDt désintégration du 1124Na suivant la loi de décroissance radioactive: N= N0e-lt. dériver par rapport au temps : dN/dt = -lN0e-lt soit dN= -lN dt ou D N2= -lN D t valeur négative bilan : DN = DN1 + D N2=QDt -lN D t à la limite : dN/dt = Q- lN soit dN/dt + lN = Q.
(1)
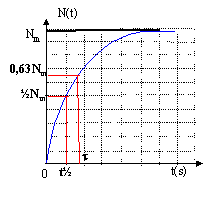
repport dans (1) : B/t e -t/t+ Bl-Ble -t/t= Q B(1/t-l)e -t/t + Bl= Q par identification Bl= Q soit 1/t-l=0 soit l=1/t et B= Q/l = Q/l =Qt. N (t) =Q/l(1-e -lt) si t tend vers l'infini N(t) tend vers Nm= Q/l ; N (t) =Nm(1-e -lt) or l t½=ln2 d'où Nm=Q t½ / ln2. à t= t½ , N(t½)= 0,5 Nm. à t= t , N(t) = 0,63 Nm.
|
||||||
|
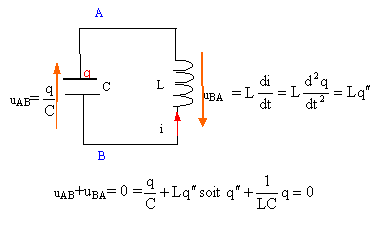
Un générateur de courant constant délivre un courant d'intensité i0 = 200 mA en étant connectées à l'ensemble d'une bobine et d'un condensateur reliés en parallèle (voir schéma). La bobine dont le coefficient d'inductance vaut L = 200 mH possède une résistance nulle. La capacité du condensateur est C= 200 nF. A l'instant t = 0 considéré comme origine des temps, on ouvre l'interrupteur K. 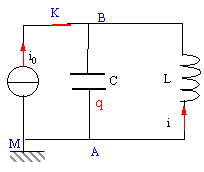
en conséquence la tension aux bornes de la bobine u=Ldi0/dt est nulle. bobine et condensateur sont en dérivation, donc la tension aux bornes du condensateur est nulle et le condensateur ne se charge pas. Par contre la bobine stocke l'énergie ½Li0² =0,5*0,2*0,2² = 4 10-3 J. donc à t=0 : intensité dans la bobine : i0 tension aux bornes du condensateur uAB=0.
charge q et tension aux bornes du condensateur sont proportionnelles : q=Cu d'où u"+ 1/(LC) u=0. on pose w0²= 1/(LC) = 1/(0,2*20010-9)= 108/4 soit w0= 5000 rad/s période T= 2 p/ w0=
2*3,14/5000 =1,256 ms.
charge q(t) = Cu(t) = CA sin (w0t + j ). dériver par rapport au temps pour obtenir l'intensité : i = CAw0cos (w0t + j ). à t=0 l'intensité vaut i0 dans la bobine : i0 = CAw0cos ( j ). i0, CAw0étant positifs on élimine la valeur j=p. A= i0 /( Cw0)= umax = 0,2/(200 10-9 *5000)=1000*0,2 = 200 V. i(t) =0,2 cos(w0t
)
échange permanent d'énergie entre bobine et condensateur : le condensateur stocke au plu s : 4 10-3 = ½Cu²max soit u²max= 8 10-3 /C = 8 10-3 / 2 10-7 =4 104 ; umax = 200 V.
|
||||||
|
Une bille sphérique de volume V = 4 cm3, de masse volumique rs = 3 g.cm-3 est lâchée sans vitesse initiale dans un liquide de masse volumique rl = 0,8 g.cm-3. On observe qu'elle a un mouvement de chute verticale.
corrigé la bille est soumise à son poids, vertical vers le bas , valeur mg=rs V g à la poussée d'Archimède, verticale vers le haut, valeur rl V g à la force de frottement verticale, vers le haut : f= kv. la seconde loi de Newton s'écrit suivant un axe vertical orienté vers le bas : rs V g -rl V g -kv = rs V dv/dt g -rl / rs g -k/(Vrs) v = dv/dt dv/dt +k/(Vrs) v =g ( 1-rl / rs) si la vitesse limite est atteinte le mouvement est rectiligne uniforme et dvlim/dt=0 k/(Vrs) vlim =g ( 1-rl / rs) vlim = g ( 1-rl / rs)Vrs /k. k= g ( 1-rl / rs) Vrs / vlim . rs = 3000 kg/m3 ; V= 4 10-6 m3 ; Vlim = 2,2 10-2 m/s. k=10(1-0,8/3) 4 10-6 *3000 / 2,2 10-2 = 10(1-0,26)*1,2/2,2 = 4 u S.I. |
||||||
|
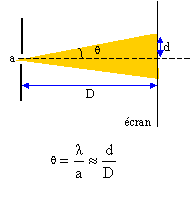
Un pinceau lumineux monochromatique, de longueur d'onde dans le vide l = 600 nm, traverse une fente de largeur a. La figure de diffraction est observée sur un écran placé perpendiculairement au pinceau lumineux à une distance D = 2m.
corrigé fréquence n = c/l = 3 108 / 600 10-9 = 5 1014 Hz. la fréquence ne dépend pas du milieu de propagation, elle caractérise la radiation.
|
||||||
|
On considère une solution d'ammoniac de concentration c.
Ke = 10-14
produit ionique de l'eau [ HO-][H3O+] = 10-14 à 25 °C [ HO-]10-pH = 10-14 ; [ HO-]=10-14 /10-pH ; [ HO-]=10pH-14 ; taux d'avancement t =[ HO-] / c =10pH-14 /c t1 = 1010,6-14 / 0,01 =10-1,4 =0,04. t2 = 1010,1-14 / 0,001 =10-0,9 =0,126 trois fois plus grand que la valeur précédente avant dilution. Qr,éq=[NH4+]éq[ HO-]éq/ [NH3]éq =(tc)² / (c(1-t))=t²c/(1-t) la constante
d'équilibre Qr,éq est constante si la température ne change
pas ; en conséquence en diluant, la concentration diminue et t va
augmenter.
|
||||||
|
Le dihydrogène peut être fabriqué en faisant l'électrolyse de l'eau acidifiée. Un procédé utilise une tension U = 2 V et une intensité I = 20 kA. L'équation de la transformation s'écrit : 2H2O (l) = 2H2 (g) + O2 (g) réaction (1)
Données. - Les couples oxydoréducteurs qui entrent en jeu dans l'électrolyse sont : O2 (g) / H2O (l) et H+ (aq) / H2 (g) - On prendra : 1 Faraday (F) = 105 C ; 1 kilowatt.heure (kWh) = 3,6 MJ Volume molaire des gaz dans les conditions de fabrication Vm = 25 L.mol-1.
x = quantité de matière H2 à la date t. don 2x = quantité de matière d'électrons à la date t. Quantité d'électricité : Q= I t = 20 000* 3600 = 7,2 107 C or la charge d'un mole d'électrons est, en valeur absolue 105 C : 7,2 107 = 2 x 105 soit x =360 mol. volume dihydrogène (L) = Qté de matière dihydrogène (mol) fois volume molaire des gaz 360*25 = 9000 L= 9 m3. énergie consommée ( kWh) : U(V) I (kA) t(h) =2*20*1 = 40 kWh |
||||||
|
On désigne par s et s' les solubilités respectives du chlorure d'argent AgCl (s) exprimées en mol.L-1 dans l'eau pure et dans une solution saturée d'ammoniac.
Données : Masses molaires en g.mol-1 : Ag 108 ; Cl : 35,5 corrigé AgCl(s)=Ag++ Cl- avec K1 =[Ag+][Cl-]=s²= 10-10 d'où s= 10-5 mol/L. masse molaire AgCl= 108+35,5 = 143,5 g/mol s= 143,5 10-5 g/L Ag+ + 2NH3 =[Ag(NH3)2]+ avec K2 = [[Ag(NH3)2]+] /( [Ag+ ][NH3]²) K2 est très grand ; la solution d'ammoniac est saturée donc [NH3] = constante. le numérateur [[Ag(NH3)2]+] est alors très supérieur au dénominateur [Ag+ ] : [[Ag(NH3)2]+] voisin s'. s'=[Ag+ total ]=[Ag+ ]+ [[Ag(NH3)2]+] = [Cl-] s' =[Ag+ ](1+[[Ag(NH3)2]+] /[Ag+ ]) = [Cl-] s' =[Ag+ ](1+K2[NH3]²) = [Cl-] s'²=[Ag+ ][Cl-](1+K2[NH3]²) = K1(1+K2[NH3]²) =K1(1+K2c²) voisin de K1K2c². s' = (K1K2)½c = (10-10*2,5 107)½*2= (25 10-4)½ * 2 =0,1 mol/L ou 14,3 g/L. valeur 104 fois plus grande que la solubilité s
dans l'eau.
|
||||||
|
|