|
d'après concours Geipi
2004
culture générale - oscillateur
non amorti - dipôle (RL) - fission et fusion - différents
ressorts - pile Cu-Ag - dipôle RC- onde
lumineuse et diffraction
|
|
|
|
- Cet été, 64000 hectares de forêt ont
brûlé en France. Cette surface est équivalente à celle d’un carré de
côté a.
- Calculer a.
- Quelle est la pression au bout du tube d’un aspirateur en
fonctionnement ? 0,7 bar ; 1,3 bar ; 3 bar ; 10 bar ; 30 bar.
- Si le Soleil se lève à 8h à Brest, à quelle heure se
lèvera-t-il à Strasbourg ? avant 8 heures ; après 8 heures.
- Avec quel décalage ? inférieur à une seconde ; compris entre 1 et 60
secondes ; compris entre 1 et 10 minutes; compris entre 10 et 30
minutes ; supérieur à 30 minutes
- Le projet international ITER a pour sujet l’étude :
Réchauffement climatique ; Fusion nucléaire ; Biotechnologies Matériaux
Supra conducteurs ; Station spatiale internationale ; Couche d’ozone.
- Classez les ondes électromagnétiques de la plus petite à la
plus grande longueur d’onde. A Rayon Gamma ; B Onde hertzienne ; C
Infra rouge ; D Lumière visible ; E Ultra violet ; F Rayon X.
- On retrouve la présence significative de plomb (Pb) dans :
le gaz carbonique ; le cristal ; une batterie de voiture ; l’eau lourde
l; ’acier inox ; le PVC
corrigé
1 ha = 104
m² ; 64 000 ha = 6,4 108 m²
côté du carré : a = 2,5 104 m.
dépression : 0,7 bar.
avant 8 heures : décalage supérieur à 30 minutes.
ITER : fusion nucléaire.
de la plus courte à la plus grande longueur d'onde ( du plus
énergétique au moins énergétique) :
A Rayon Gamma ; F Rayon X ; E Ultra violet ; D Lumière visible
; C Infra rouge ; B Onde hertzienne.
présence significative de plomb : cristal ; batterie de
voiture.
|
|
sujet 2
On étudie le mouvement d’un oscillateur non amorti constitué
d’un solide (S) de masse M = 300 g, lié à un ressort dont l’autre
extrémité est fixe. Le solide (S) peut se déplacer en translation
rectiligne sans frottement selon l’axe Ox horizontal. Le mouvement du
centre d’inertie de (S) enregistré à l’aide d’un ordinateur est
représenté sur la figure ci-dessous.
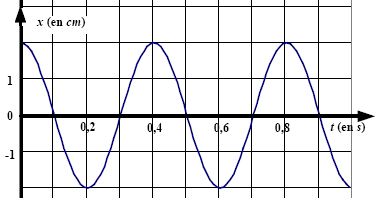
Son équation horaire est de la forme : x = A cos (wt +f) avec x
l’élongation , A l’amplitude des oscillations, T= 2p/w= la période des oscillations et f la phase. A l’instant t = 0 le solide (S) est
libéré sans vitesse initiale, le ressort étant étiré.
- Calculer la fréquence f du mouvement.
- Ecrire l’équation horaire de la vitesse et la calculer pour
l’instant t = 0,5 s.
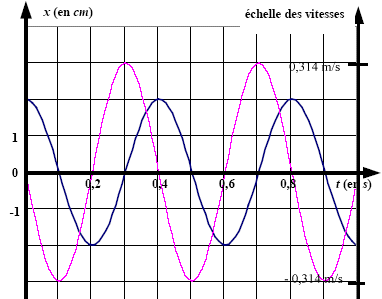
- Calculer les vitesses maximale Vmax et minimale Vmin.
Tracer la courbe représentant la vitesse en fonction du temps.
- Calculer l’accélération a et la force Fr
agissant sur le solide à l’instant t = 0.
- On ajoute une surcharge m au solide (masse totale M+m) et
on libère sans vitesse avec la même élongation que dans l’expérience
précédente. On note que la période a augmenté de10%. Quelle est la
valeur de la masse m de la surcharge ?
corrigé
période T= 0,4 s ( lecture graphe)
fréquence f = 1/T
= 1/0,4 = 2,5 Hz.
La vitesse v(t)
est la dérivée de x(t) par rapport au temps :
x = A cos (wt +f)
; v(t) = -Aw
sin (wt +f)
Vmax = Aw avec A= 0,02 m (lecture graphe) et w = 2p/T=
2*3,14/0,4=15,7 rad/s
Vmax =
0,02*15,7 = 0,314
m/s ; Vmini
=-Aw = -0,314 m/s.
l'accélération est la dérivée de la vitesse par rapport au
temps : a(t) = -A w² cos
(wt +f) = -w² x(t)
a(t=0) = -w² x(t=0)=
-w²A= - 15,7² *0,02 = -4,9
m/s² ( le signe moins indique que l'accélération à le sens
contraire de l'axe Ox)
force de rappel à t=0 : Fr =Ma(t=0) = -MAw² = -0,3*4,9 = -1,48 N.
période T= 2p [M/k]½
soit t² = 4p²M / k.
avec surcharge :T '= 2p [(M+m)/k]½
soit T '² = 4p²(M+m)/k.
T '² / T² = (M+m) / M = 1+m/M
T ' /T= [1+m/M]½ avec T ' / T = 1,1 et T '² / T²
=1,1² = 1,21.
1+m/M= 1,21 soit : m= 0,21 M= 0,21*0,3 = 0,063 kg = 63 g.
|
|
sujet 3 :
On étudie le montage suivant. Initialement K1 et K2
sont ouverts depuis un temps très long, la bobine est considéré comme
idéale (sa résistance interne est nulle).
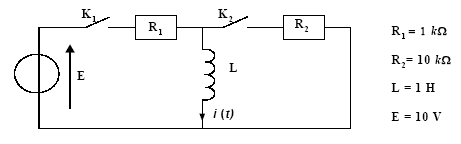
A t = 0, on ferme l’interrupteur K1, l’interrupteur
K2 reste ouvert.
- Ecrire l’équation différentielle vérifiée par le courant i
(t) dans la bobine.
- La solution de cette équation différentielle est de la
forme i(t) =A +Bexp(-t/t), donner les
expressions littérales de A, B et t. Donner
la valeur numérique de t.
- Donner la valeur numérique de i (t) pour t = 0,5 ms et pour
t = 5 ms.
A t = T on ouvre K1 et on ferme K2 de façon
simultanée.
- En prenant une nouvelle origine des temps telle que t'= 0
corresponde à t = T, écrire l’équation différentielle vérifiée par i
(t') , courant dans la bobine.
- La solution de cette équation différentielle est de la
forme i(t') =A' +B'exp(-t'/t'), donner
l’expression littérale de t'. Que vaut A' ?
Donner la valeur numérique de t' .
- Indiquer la valeur numérique de B' dans les deux cas
suivants : T= 0,5 ms et pour T = 5 ms.
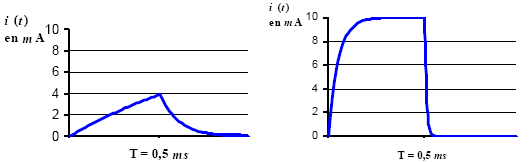
- Tracer l’allure de i (t) dans les deux cas suivants : T =
0,5 ms et pour T= 5 m
corrigé
E= R1i + Ldi /dt
solution de cette équation différentielle : i(t) =A +Bexp(-t/t),
avec t = L/R1 = 1/1000
= 1 ms = 10-3 s.
A valeur du courant en régime permanent : A = E/R1
= 10*/1000 = 0,01 A = 10 mA et B= -A.
i(t=0,5 ms)= 0,01(1-exp(-0,5/1))= 3,94
mA.
i(t=5 ms)= 0,01(1-exp(-15/1))= 9,93 mA.
Ldi/dt + R2i=0
solution de cette équation différentielle : i(t') =A'
+B'exp(-t'/t'),
avec t' =
L/R2 = 1/10000 = 0,1 ms = 10-4
s.
B' valeur initiale de l'intensité à t= T, fermeture de K2,
ouverture de K1.
B'= 3,94 mA si T= 0,5 ms ; B'= 9,93 mA si T= 5 ms.
|
|
sujet 4
Première partie : fission de l’uranium
Parmi les réactions, très variées, de fission de l’atome
d’uranium 235 bombardé par des neutrons lents, on considère la réaction
suivante : 235 92U + 01n-->
139 xXe +94 38Sr + y01n
- Compléter l’équation en calculant x et y.
- À partir du tableau placé à la fin de l’énoncé, calculer :
a) l’énergie E, en joules puis en MeV, libérée par la fission d’un
noyau d’uranium 235,
b) l’énergie E', en joules, libérée par la fission d’une masse M = 1 kg
d’uranium 235.
Deuxième partie : Fusion de l’hydrogène
- L’hydrogène possède trois isotopes stables11H,
21H et 31H,
- Ecrire les différentes réactions qui, à partir de deux noyaux
d’isotopes identiques ou différents, conduisent à la formation d’un
noyau d’hélium accompagné ou non d’une ou plusieurs particules
- Parmi ces possibilités, on s’intéresse à celle qui produit un neutron
en plus du noyau d’hélium. A partir des données de l’énoncé :
a) encadrer la réaction correspondante parmi celles écrites dans le
document réponse
b) calculer l’énergie E, en joules, accompagnant la production d’un
noyau d’hélium,
c) calculer l’énergie E' libérée par la fusion totale d’une masse M = 1
kg de mélange contenant le même nombre d’atomes des deux isotopes.
Troisième partie : comparaison des deux procédés
Cocher dans le tableau du document réponse, les cases
correspondantes aux réponses qui vous semble correctes.
|
fission
|
fusion
|
|
Plus grande abondance des réserves de combustible
|
|
|
|
Production moindre de déchets radioactifs
|
|
|
|
Pas de risque d’emballement des réactions
|
|
|
|
Technologie utilisée en production industrielle
|
|
|
Données : 1 u = 1,67 10-27 kg, c = 3 108
m.s-1, e = 1,6 10-19 C. On néglige la masse des
électrons.
|
noyau ou particule
|
23592U
|
139xXe
|
9438Sr
|
10n
|
21H
|
31H
|
42He
|
|
masse (u)
|
235,044
|
138,918
|
93,915
|
1,009
|
2,013
|
3,015
|
4,001
|
corrigé
235 92U + 01n-->
139 xXe +94 38Sr + y01n
conservation de la charge : 92 = x+38 soit x= 54
conservation du nombre de nucléons : 235 +1= 139+94+y soit y =
3.
diminution de masse |Dm|=235,044-(138,918+93,915+2*1,009)=0,193
u = 0,193*1,67 10-27 = 3,223 10-28 kg.
énergie libérée E= |Dm| c² = 3,223
10-28 * (3 108)²=2,9 10-11
J=2,9 10-11 / 1,6 10-19 = 1,81 108
eV= 181 MeV.
énergie libérée pour 1 kg d'uranium 235 :
235,044*1,67 10-27 = 3,92 10-25 kg
1 / 3,92 10-25 = 2,55 1024 réactions de
fission
E' = 2,55 1024 * 2,9 10-11 = 7,4 1013 J.
21H + 21H -->42He
11H + 31H -->42He
21H + 31H -->42He + 10n
31H + 31H -->42He +2 10n
diminution de masse |Dm|=2,013+3,015-(4,001+1,009)=0,018
u = 0,018*1,67 10-27 = 3 10-29 kg.
énergie libérée E= |Dm| c² = 3 10-29
* (3 108)²=2,7 10-12
J
énergie libérée pour 1 kg des deux isotopes :
(2,013+3,015)*1,67 10-27 = 8,4 10-27 kg
1 / 8,4 10-27 = 1,19 1026 réactions de
fusion
E' = 1,19 1026 * 2,7 10-12 = 3,2 1014 J.
|
fission
|
fusion
|
|
Plus grande abondance des réserves de combustible
|
|
x
|
|
Production moindre de déchets radioactifs
|
|
x
|
|
Pas de risque d’emballement des réactions
|
|
x
|
|
Technologie utilisée en production industrielle
|
x
|
|
|
|
sujet 5
On considérera dans ce problème des ressorts à spires non
jointives et de masses négligeables. Les extrémités des ressorts se
situeront sur un axe horizontal. Soit un solide (S) de masse M et
d’épaisseur négligeable est accroché aux ressorts. Les seules forces
agissant sur cet objet seront exercées par les ressorts. Premier cas :
Le solide (S) est accroché à un seul ressort (de raideur k et de
longueur au repos l0) et dont l’autre extrémité est fixe.
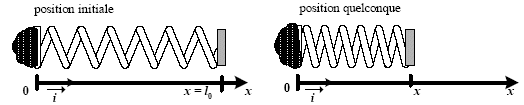
- Ecrire l’équation différentielle du mouvement de (S) de
masse M.
- Donner l’expression de la période T du mouvement.
- Deuxième cas : Le solide (S) est accroché à deux
ressorts. Le ressort 1 de gauche a une raideur k1 et une
longueur au repos l0. Le ressort 2 de droite a une raideur k2
et une même longueur au repos l0. Les extrémités des
ressorts non liées à (S) sont fixes.
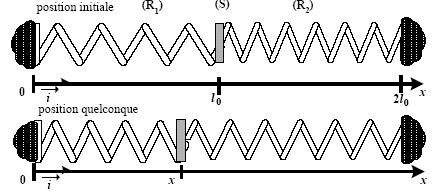
Donner l’expression des forces s’exerçant sur (S).
En déduire l’équation différentielle du mouvement.
Cette association de deux ressorts est équivalant à un ressort unique
de raideur keq. Donner l’expression de keq .
- Le solide (S) est accroché au ressort (R2) de
raideur k2 et de longueur au repos l02. L’autre
extrémité de (R2) est liée au ressort (R1) de
raideur k1 et de longueur au repos l01. L’autre
extrémité (R1) est fixe.
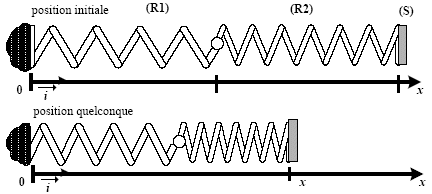
Comparer la force exercée par le ressort 2 sur (S) R2/SF
à la force exercée par le ressort 1 sur le ressort 2 FR1/R2.
Cette association de deux ressorts est équivalant à un ressort unique
de raideur k'eq et de longueur à vide l0 eq.
Donner les expressions de l0 eq. et k'eq.
corrigé
équation différentielle du mouvement de
S : k(x-l0) + mx"=0 ou x"+ k/m (x-l0) =0
période T= 2p (m/k)½.
tension du ressort 1 : T1 = k1(l0-x),
horizontale vers la droite
tension du ressort 2 : T2 = k2(2l0-x-l0)=
k2(l0-x), horizontale vers la droite
équation différentielle : k1(l0-x) + k2(l0-x)
= mx"
( k1+ k2)(l0-x) = mx",
raideur équivalente : keq = k1+ k2.
même valeur R2/SF = FR1/R2 et
même sens.
longueur à vide du ressort unique équivalent : l0 eq
= l0 1 + l0 2.
raideur équivalente : k'eq = k1 k2
/ ( k1+ k2)
|
|
sujet 6
On souhaite réaliser une pile faisant intervenir les couples
oxydant/réducteur du cuivre et de l’argent : Cu2+ / Cu et Ag+
/ Ag. Dans une expérience préliminaire, chacun des métaux est plongé
dans une solution contenant des ions de l’autre élément :
a) lorsqu’un fil d’argent est plongé dans une solution de
chlorure de cuivre II, on n’observe aucune transformation.
b) lorsqu’une lame de cuivre est plongée dans une solution de
nitrate d’argent, elle se couvre d’une couche noirâtre et la solution
prend une teinte bleutée.
- Ecrire l’équation d’oxydoréduction faisant intervenir les
quatre espèces chimiques dans le sens de transformation auquel
correspond la constante d’équilibre K = 4 1015.
- On réalise une pile : Ag /Ag+ // Cu2+
/ Cu selon le schéma ci-dessous :
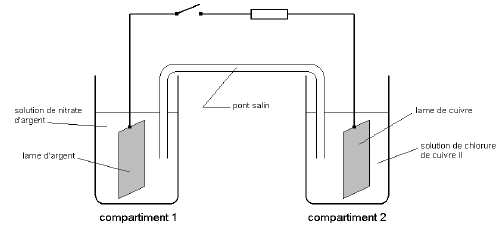
Chaque compartiment contient 20mL d’électrolyte de
concentrations respectives en cations : [Ag +]0
= 0,1 mol.L-1 et [Cu2+]0 = 0,1 mol.L-1.
Le pont salin contient une solution gélifiée de chlorure de sodium à 1
mol.L-1.
-Calculer le quotient de réaction Qr initial au début de l’expérience
(interrupteur ouvert).
On relie les électrodes par un conducteur ohmique (en fermant
l’interrupteur).
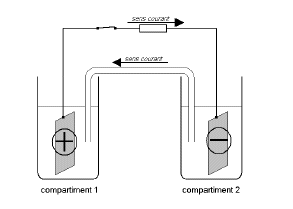
- Préciser sur le schéma le sens du courant dans la branche comportant
le résistor et dans le pont salin ; indiquer la polarité des électrodes.
On laisse débiter la pile pendant 90 minutes ; on mesure au bout de ce
temps une variation de masse de l’électrode d’argent de 30 mg.
-Calculer la quantité d’électricité Q fournie par la pile pendant ces
90 minutes.
- En considérant que la conduction ionique est assurée essentiellement
par les espèces du pont salin, calculer les concentrations en ions dans
chaque demi-pile au bout de 90 minutes.
- Si on poursuit longtemps l’expérience, on observe l’intensité
diminuer progressivement jusqu’à ce que la pile s’arrête de débiter.
Donner alors la valeur prise par le quotient de réaction Qr final.
- Calculer l’avancement final de la réaction.
Données : Masses molaires (g/mol): N: 14 ; O : 16; Cl= 35,5 ; Cu : 63,5
; Ag = 108
Constante d’Avogadro : NA = 6,023.1023 mol-1
; faraday : 1 F = 96500 C ; charge élémentaire : e = 1,6.10-19
C.
corrigé
l’argent se couvre d’une couche noirâtre
et la solution prend une teinte bleutée :
la réaction spontanée est : Cu(s) + 2Ag+ = Cu2+
+ 2Ag(s)
cette réaction est celle du bilan du fonctionnement de la pile.
Qr i = [Cu2+]0/[Ag+]02=0,1
/ 0,1² = 10
Qté de matière d'argent deposé : 0,03/108 = 2,78 10-4 mol
Or la réduction de Ag+ ( Ag+ + e-
=Ag) met en oeuvre un électron : donc 2,78 10-4 mol
d'électrons.
La charge d'une mole d'électrons vaut, en valeur absolue 96500
C
Qté d'électricité : 96500*2,78 10-4 = 26,8 C.
les ions argent disparaissent ( compartiment
1) : -2,78 10-4 mol:
0,1*0,02=2 10-3 mol d'ion argent initialement
2 10-3 - 2,78 10-4 = 1,72 10-3
mol dans 20 mL
[Ag+]= 1,72 / 20 = 0,086
mol/L.
[NO3-]=0,1 mol/L en conséquence la
solution du compartiment étant électriquement neutre, les ions sodium
migrent du pont salin dans le compartiment 1. [Na+]=
0,1-0,086 = 0,014 mol/L.
les ions cuivre apparaissent ( compartiment 2)
: +½*2,78 10-4 = 1,39 10-4 mol
0,1*0,02=2 10-3 mol d'ion cuivre II initialement
2 10-3 + 1,39 10-4 = 2,14 10-3
mol dans 20 mL
[Ag+]= 2,14 / 20 = 0,107
mol/L.
la solution du compartiment étant électriquement neutre, les
ions chlorure migrent du pont salin dans le compartiment 2.
2[Cu2+]=[Cl-]= 2*0,107 =0,214 mol/L.
Qr= [Cu2+]/[Ag+]2
avec [Cu2+] croissante et [Ag+] décroissante
Qraugmente : valeur prise par le quotient de
réaction Qr final = K= 4 1015.
|
Cu(s)
|
+ 2Ag+
|
=Cu2+
|
+ 2Ag(s)
|
|
initial
|
supposé en excès
|
0,02*0,1 = 2 10-3 mol
|
0,02*0,1 = 2 10-3 mol
|
n
|
|
en cours
|
2 10-3 -2x
|
2 10-3 -x
|
n+2x
|
|
final
|
2 10-3 -2xf =0
|
2 10-3 -xf
|
n+2xf
|
xf = 10-3 mol.
|
|
sujet 7
La réalisation de cartes de circuits électroniques nécessite
la production d’un éclair délivrant une énergie E= 11,5 J pendant une
durée TE= 2,3 ms. Cet éclair est émis, à l’aide du montage
ci-dessous, par le tube à éclair d’un flash électronique. L’énergie
provient de la décharge d’un groupement série de condensateurs
identiques. Le groupement a une capacité équivalente totale CN
= 100 µF. La tension à ses bornes, avant décharge, est notée U0.
- Donner la valeur numérique : a) PE de la
puissance électrique mise en jeu durant un éclair ;
b) U0 de la tension avant décharge.
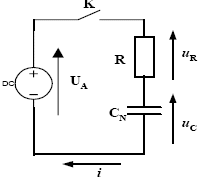
- On procède à une vérification expérimentale de la valeur de
la capacité totale CN à l’aide du montage suivant où R est
une résistance de forte valeur et UA une tension continue de
6V. A l’instant t = 0, le condensateur étant déchargé, on ferme
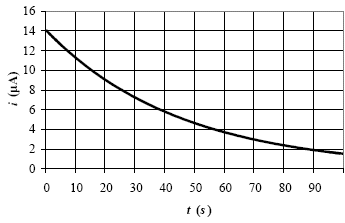
l’interrupteur K et on relève alors l’évolution i = f (t)du courant i
en fonction du temps t. On en donne, ci-après, la courbe représentative.
Donner les valeurs numériques : a) UC (0) de la tension uC
(t) à l’instant t = 0 ;
b) UR (0) de la tension uR (t) à l’instant t = 0 ;
c) R de la résistance.
- Choisir, parmi les équations proposées, celle représentant
l’évolution du courant i. I0 est la valeur du courant i(t) à
l’instant t = 0. La constante de temps de ce circuit est notée t=RCN.
i(t) = I0 (1-exp(-t/t)) ; i(t) = I0
(1+exp(-t/t)) ; i(t) = I0 exp(-t/t) ; i(t) = I0 exp(+t/t) ;
A partir de la courbe i = f(t) et en utilisant la valeur particulière
i(t) du courant à l’instant t = t,
déterminer la valeur numérique expérimentale de la capacité CN.
corrigé
puissance électrique mise en jeu durant
un éclair = énergie (J) / durée (s)=11,5/2,3 10-3 = 5000 W.
énergie stockée par le condensateur : E=½CU²0 soit U0
= (2E/C)½=(2*11,5 / 10-4 )½ = 480 V.
à t = 0 le condensateur est déchargé et l'intensité du courant
vaut 1,4 10-5 A : la tension à ses bornes uC est nulle.
la tension aux bornes du résistor vaut 6= uC+uR
soit uR=6 V.
uR=R i soit R= 6 / 1,4 10-5 = 4,28 105 ohms.
i(t) = I0 exp(-t/t)
tracer la tangente à l'origine du graphe i(t) ; elle coupe
l'axe des temps à t=t = 50 s.
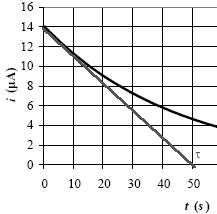
50 =R CN soit CN= 50 / 4,28 105
= 1,17 10-4 F soit 117 mF.
|
|
sujet 8
Un laser émet des impulsions lumineuses, de longueur d’onde l = 633 nm, qui sont transportées par une fibre
optique de longueur L = 250 m. Un récepteur est disposé à l’entrée de
la fibre, et un autre à la sortie de la fibre optique. Ils permettent
de détecter le passage des impulsions lumineuses et de les visualiser
sur l’écran d’un oscilloscope. Le dispositif est schématisé ci-dessous.
On rappelle que la célérité de la lumière dans le vide est c = 3,00.108m.s-1.

On observe à l’oscilloscope les signaux ci-dessous, la vitesse
de balayage étant 0,200 µs / div :
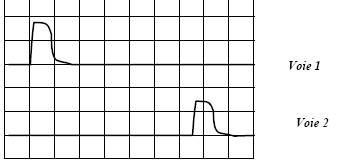
- Quel est le domaine de longueurs d’onde correspondant à la
lumière visible ?
- Calculer les fréquences limites de la lumière visible.
- A partir de l’enregistrement des signaux captés par les
deux récepteurs, calculer la célérité v de la lumière émise par le
laser dans la fibre optique.
- En déduire l’indice de réfraction n du matériau dont la
fibre est constituée.
- Préciser comment varient les caractéristiques suivantes
lorsque le faisceau du laser passe de l’air dans la fibre : a)
fréquence b) longueur d’onde c) célérité d) couleur.
- On fait maintenant fonctionner le même laser en continu, et
on place sur le trajet du faisceau émis par le laser un cheveu
d’épaisseur e. On enregistre l’intensité lumineuse reçue le long d’un
axe horizontal sur un écran perpendiculaire au faisceau du laser, placé
à une distance D = 32 cm après le cheveu, et on obtient la courbe
présentée page suivante (l’intensité lumineuse dans la région centrale
est tellement importante que le capteur est saturé).
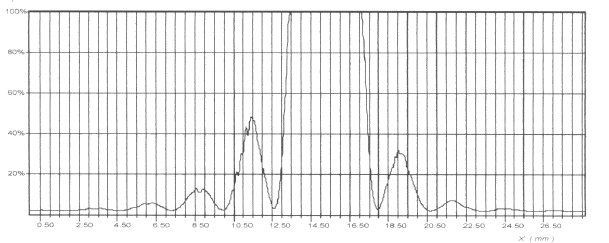
a) Comment appelle-t-on le phénomène observé ?
b) On propose plusieurs relations entre la largeur d de la tache
centrale, D, l et l’épaisseur e du cheveu.
Choisir la relation exacte. Ecrire l’équation aux dimensions de la
solution que vous avez retenue.
d= 2lD/e ; d=l/e
; d=2D/(le) ; d= e/(2l)
; d= eD/l.
c) Calculer l’épaisseur e du cheveu.
d) Quelle serait la largeur approximative de la tache centrale si on
utilisait un laser émettant de la lumière bleue au lieu de lumière
rouge ?
corrigé
Domaine des longueurs d'onde du visible
: de 400 nm à 780 nm.
fréquences limites f = c/l.
fUV = 3 108 / 400 10-9 = 7,5 1014 Hz.
fIR = 3 108 / 780 10-9 = 3,84 1014 Hz.
Dt = 6,5 *0,2
10-6 = 1,3 10-5 s ; L= 250 m ; v= 250/1,3 10-5
= 1,92 107 m/s.
indice de réfraction = rapport des vitesses = 3 108/1,92
108 = 1,56.
la fréquence reste identique, donc la couleur reste identique.
la célérité diminue donc la longueur d'onde augmente (l= v/f)
phénomène de diffraction
d= 2lD/e ;
l : mètre [m] ; D mètre [m] ; e
mètre [m] donc d en mètre
épaisseur du cheveu : e= 2lD/ d
la tâche centrale a une largeur voisine de 5
mm ( lecture graphe) soit d= 5 10-3 m ; D= 0,32
m et l= 633 10-9 m
e= 2*633 10-9 *0,32 / 5 10-3 = 8 10-5
m = 80 mm.
en lumière bleue l voisin 450 nm :
d= 2lD/e = 2*450 10-9*0,32/
80 10-6 = 3,6 10-3 m =3,6
mm.
|
|
retour -menu
|