1. Un cycliste de masse m=78 kg aborde avec une vitesse de 20 km/h une descente rectiligne de longueur 800 m et inclinée d'un angle a par rapport à l'horizontale.On modélisera les frottements par une force unique de valeur constante 40N directement opposée au vecteur vitesse. Au bas de la pente la vitesse du cycliste est 90 km/h. Déterminer a en degré. ( 3 ; 5 ; 7; 9 ; 11 ; aucune réponse exacte)
   travail moteur du poids en decente mgL sin a = 78*9,8*800 sin a =6,11 10⁵ sin a ;
   tavail résistant des frottement : -f L= -40*800 = -3,2 10⁴ J
   énergie cinétique initiale : ½mv_i²avec v_i = 20/3,6 =5,56 m/s. ½mv_i²= 0,5*78*5,56²= 1206 J
   énergie cinétique finale : ½mv_f²avec v_f = 90/3,6 =25 m/s. ½mv_f²= 0,5*78*25²= 2,44 10⁴ J
   variation énergie cinétique = 2,32 10⁴ J
   2,32 10⁴ = -3,2 10⁴ +6,11 10⁵ sin a ; soit 5,1 degrés.
   
2. Combien d'affirmations sont exactes ?
   a- Le niveau de référence pour lequel l'énergie potentielle de pesanteur est nulle est choisi arbitrairement.
   b- l'énergie potentielle de pesanteur est définie à une constante près, seules ses variations sont déterminées.
   c- L'énergie potentielle de pesanteur est une grandeur algèbrique, elle peut être négative.
   d- La variation de l'énergie potentielle de pesanteur dépend du choix du niveau de référence.
   e- Si l'énergie mécanique du solide reste constante alors la variation d'énergie potentielle de pesanteur est égale à la variation d'énergie cinétique
   d et e sont fausses.
   
   
3. On considère une photopile de surface 120 cm² exposée dans un lieu qui reçoit en moyenne une énergie solaire au niveau du sol de 1400 kWh m^-2 par an. Dans ces conditions la photopile fournit une puissance électrique de 600 mW. Donnée : 1 Wh = 3600 J. Calculer le rendement (en %) de cette photopile. (27,4 ; 31,3 ; 34,2 ; 37,8 ; 39,5 ; aucune réponse exacte) 120 cm² = 0,012 m²
   puissance solaire par m² : 1400 *1000 *3600 / ( 365*24*3600)=1,4 10⁶ / (365*24)=159,8 W m^-2.
   puissance photopile par m² : 0,6 / 0,012 = 50 W m^-2.
   rendement 100* 50/159,8 = 31,3 %
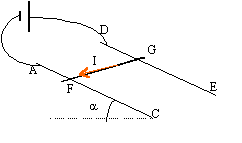
4. Une tige de cuivre homogène FG, de masse m et de longueur L peut glisser sans frottement sur deux rails en cuivre Ac et DE. La tige reste toujours perpendiculaire aux rails et maintient entre eux le contact électrique. L'ensemble est plongé dans un champ magnétique uniforme orthogonal au plan formé par les rails Ac et DE, dirigé vers le haut, de valeur B. On relie les rails à un générateur de tension qui débite un courant continu d'intensité I.
   Données : L= 12 cm ; B= 0,4 T; m=150g ; a = 15°.

   Combien d'affirmations sont exactes ?
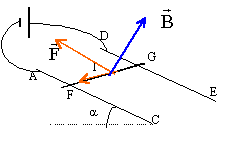
   a- La force de Laplace s'exerçant sur la tige FG s'applique au milieu de cette tige.
   b- La direction de la force de Laplace est parallèle aux rails AC et DE
   c- Le sens de la force de Laplace est vers le haut du schéma
   d- La valeur de la force de Laplace se calcule par la relation F=I B L
   e- Dans cette expérience il y a conversion d'énergie mécanique en énergie électrique

   e- est fausse, énergie électrique convertie en énergie mécanique
   
5. Déterminer la valeur de l'intensité I (en A) du courant pour que la tige soit en équilibre.
   7,9 ; 10,5 ; 14,8 ; 20,6 ; 27,2 ; aucune réponse correcte.
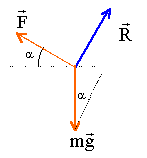
   à l'équilibre la tige est pseudo-isolée:
   La somme des vecteurs forces s'écrit en projection sur un axe parallèle au plan orienté vers le haut.
   F=I L B= m g sin a.
   I= m g sin a / (B L)= 0,15*9,8*sin15/(0,4*0,12)= 7,9 A.
   
6. On utilisait autrefois comme unité d'activité le curie (symbol Ci). Un curie correspond à l'activité d'une source contenant 1 g de radium.
   Données : demi-vie du radium 1590 ans ; masse atomique molaire du radium M = 226 g/mol ; N_A= 6,02 10²³ mol^-1.
   Déterminer la valeur de 1Ci en GBq. ( 8 ; 16 ; 22 ; 25 ; 37 ; aucune bonne réponse) 1/226 = 4,42 10^-3 mol de radium
   N= 4,42 10^-3 * 6,02 10²³ = 2,66 10²¹ noyaux de radium dans 1 g.
   lt½=ln2 = 0,693 soit l = 0,693 / (1590*365*24*3600)= 1,38 10^-11 s^-1.
   activité de 1 g de radium : A= l N= 1,38 10^-11 *3,67 10²¹ = 36,7 10¹⁰ Bq= 36,7 GBq.
7. Le polonium ²¹⁰₈₄Po subit une désintégration de type a. ²¹⁰₈₄Po = ²⁰⁶₈₂Pb + ⁴₂He
   masse des noyaux en u : ²¹⁰₈₄Po = 210,0482 ; ²⁰⁶₈₂Pb =206,0385 ; ⁴₂He = 4,0015
   1 u = 1,66 10^-27 Kg ; c= 3 10⁸ m/s. demi vie du polonium 210 : 138 jours
   Déterminer l'activité ( en Bq) d'un échantillon de polonium 210 dégageant une puissance P= 500 mW
   ( 2,4 10⁴ ; 3,5 10⁵ ; 2,7 10⁸ ; 5,1 10⁹ ; 4,1 10¹⁰ ; aucune réponse exacte. variation de masse |Dm|=|210,0482-4,0015-206,0385 |= 8,2 10^-3 u= 8,2 10^-3* 1,66 1^0-27 =1,36 10^-29 kg
   énergie libérée par chaque désintégration : |Dm| c² = 1,36 10^-29 *9 10¹⁶=1,22 10^-12 J
   énergie (J) libérée par N noyaux en une seconde 0,5 J /s.
   d'où N= 0,5 /1,22 10^-12 = 4 10¹¹ noyaux
   lt½=ln2 = 0,693 soit l = 0,693 / (138*24*3600)= 5,81 10^-8 s^-1.
   activité A =l N=5,81 10^-8 * 4 10¹¹ = 2,32 10⁴ Bq.
   

   ---

   ---

8. Une lampe spectrale émet un rayonnement de longueur d'onde l=366 nm. La quantité de photons émis par heure est N= 332 mmol /h.Données : h= 6,62 10^-34 Js ; c= 3 10⁸ m/s ; nombre d'Avogadro 6,02 10²³ mol^-1.
   Déterminer la puissance (en W) avec laquelle la lampe émet ce rayonnement (5,2 ; 16,4 ; 30,1 ; 32,3 ; 38,1 ; aucune réponse exacte) énergie d'un photon : E=hc/l= 6,62 10^-34*3 10⁸ / 366 10^-9 = 5,43 10^-19 J
   nombre de photons émis par seconde :
   0,332*6,02 10²³ /3600 = 5,55 10¹⁹ photons
   énergie libérée en une seconde : 5,55 10¹⁹* 5,43 10^-19 = 30,1 W
9. On peut modéliser une loupe par une lentille mince convergente. Une personne désire voir 5 fois plus grand les caractères d'un livre. La vergence de la lentille est C=7 d. Déterminer à quelle distance ( en cm) le lecteur doit placer sa loupe.(2,8 ; 11,4 ; 14,2 ; 17,8 ; 21,2 ; aucune réponse exacte) toutes les grandeurs sont algébriques
   l'image est virtuelle et le grandissement vaut donc +5 = OA'/OA soit OA'=5 OA
   relation de conjugaison : 7 =1/OA'-1/OA soit 7=1/(5OA)-1/OA
   7= -4 /(5OA) ; OA= -4/ (7*5)= -0,114 m = -11,4 cm.
   distance loupe-journal : 11,4 cm.
10. Un oscillateur est constitué par un solide S ponctuel de masse M accroché à l'extrémité d'un ressort à spires non jointives, de masse négligeable et de constante de raideur k. S oscille sans frottement sur une table horizontale.
    On repère la position à l'instant t de S sur un axe horizontal dont l'origine correspond à la position de S au repos. On écarte S de 3 cm de sa position d 'équilibre dans le sens des abscisses positives et on le lâche sans vitesse initiale. L'origine des temps est prise au premier passage du solide S par la position d'équilibre. L'équation horaire est de la forme x(t) = X_m cos (2p/T₀t+j).
    données: M=150g ; k=20 N/m
    Déterminer l'énergie cinétique (en mJ) à la date t=0,3 s.(8,1 ; 12,3 ; 16,4 ; 21,6 ; 31,4 ; aucune réponse exacte) période T₀= 2*3,14 racine carrée (0,150/20)=0,544 s et 2p/T₀ = 11,54 rad/s
    vitesse, dérivée de x par rapport au temps v(t)=X_m (-2p/T₀)sin (2p/T₀t+j).
    à t=0 la vitesse est maximale et l'abscisse est nulle
    x(0) =0= X_m cos (j) d'où j= ½p ou 3p/2.
    v(0)=X_m (-2p/T₀)sin (j) avec X_m = 0,03 m
    le solide se déplace en sens contraire de l'axe donc j = p/2
    v(0,3 )=0,03 (-11,54)sin (11,54*0,3+p/2).
    v(0,3 ) = -0,346 *(-0,95) = 0,328 m/s
    énergie cinétique :½mv²=0,5*0,15*0,328²= 8,1 10^-3 J= 8,1 mJ. 

Une bille d'acier de masse m et de rayon r est lâchée à la date t=0 sans vitesse initiale dans une éprouvette graduée contenant de la glycérine. le mouvement du centre d'inertie G de la bille est repéré sur l'axe (Oz). L'origine zéro correspond à la position du centre d'inertie à t=0. Un dispositif informatisé permet de représenter la vitesse v du centre d'inertie de la bille en fonction du temps. Au cours de la chute la bille est soumise à :

- son poids P

- à la poussée d'Archimède P

- à une force de frottement fluide f= kv avec k= 6prh.

L'équation différentielle du mouvement se met sous la forme dv/dt + k/m v-g(1-r₀/r)=0

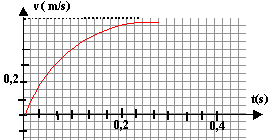
On admet que le mouvement de la bille est rectiligne uniforme après une durée égale à 5 t avec t = m/k.

1. Déterminer graphiquement la valeur de la vitesse limite v_l (m/s)
2. Etablir l'expression littérale de la vitesse limite en fonction de r₀, r, h, r et g.
3. Calculer le rayon r de la sphère en mm
   viscosité de la glycérine h = 1,5 Pa s ; masse volumique glycérine : r₀ =1,26 g/mL ; masse volumique acier : r= 7800 kg/m³. volume sphère 4/3 p r³. g =9,8 m/s² ; hauteur de chute h=80 cm
4. Pendant le régime transitoire z(t) est de la forme z(t) = v_l t + t v_l (e ^-t/t-1)
   - Calculer la distance h₁ ( en cm) parcourue par la bille à la fin du régime transitoire.
5. En déduire la durée Dt de la chute de la bille.

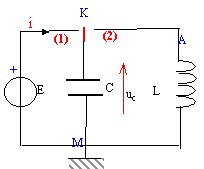
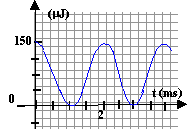
L'interrupteur en position 1 permet dans un premier temps de connecter le condensateur de capacité C aux bornes d'un générateur de fem E= 10 V. Lorsque le condensateur est chargé on bascule l'interrupteur en position 2. On suppose que les oscillations électriques ne sont pas amorties. On désigne par u_c la tension aux bornes du condensateur. Un dispositif informatique permet d'étudier l'énergie stockée dans le condensateur en fonction du temps.

1. Calculer la valeur de la capacité du condensateur ( en mF)
2. Déterminer la période propre T₀ des oscillations ( en ms).
3. En déduire la valeur de l'inductance L ( en mH) de la bobine.
4. Calculer la valeur maximale de l'intensité du courant ( en mA) dans le circuit.
5. Déterminer par une méthode de votre choix l'énergie stockée dans le condensateur ( en m J) lorsque l'intensité est égale à 25 % de sa valeur.

 masse atomique molaire (g/mol) Ag= 107,9 ; C=12 ; Ba= 137,3 ; O=16 ; H=1 Na=23 ; S=32 ; Cl=35,5.

1. On veut déterminer le pourcentage massique en hydroxyde de sodium d'un déboucheur de canalisation ménager. On réalise le dosage de 10 mL d'une solution obtenue en diluant 50 fois la solution commerciale de déboucheur par une solution d'acide chlorhydrique de concentration c_A= 0,1 mol/L. Il faut verser un volume V_Aéq = 15 mL de solution d'acide chlorhydrique pour obtenir l'équivalence.
   Donnée : densité par rapport à l'eau de la solution du déboucheur d=1,2.
   Calculer le pourcentage massique d'hydroxyde de sodium de la solution commerciale. ( 5 ; 11 ; 20 ; 25 ; 33 ; aucune réponse exacte) C_aV_Aéq=C_bV_b soit C_b = C_aV_Aéq/V_b =0,1*15/10=0,15 mol/L
   en tenant compte de la dilution : 50*0,15 = 7,5 mol/L
   masse de soude 7,5*40 = 300g
   masse de 1 L de solution : 1200 g
   soit 300/1200*100 = 25% en masse de soude.
2. L'équation de dissolution du sulfate de baryum s'écrit : BaSO₄ (s) = Ba²⁺ + SO₄^2-. La constante d'équilibre associée est : K= 10^-10 à 25°C. On définit la solubilité du sulfate de baryum dans l'eau comme la masse minimale de solide qu'il est possible de dissoudre dans 1 L d'eau à 25°C.
   Calculer la solubilité du sulfate de baryum ( en mg/L) (2,3 ; 3,4 ; 7,5 ; 12,6 ; 5,8 ; aucune bonne réponse) K=[Ba²⁺][SO₄^2-]=s²=10^-10 d'où s= 10^-5 mol/L
   masse molaire sulfate de baryum 233,3 soit 233,3*10^-5 = 2,33 10^-3 g/L= 2,33 mg/L
3. La masse d'une pastille d'hydroxyde de sodium solide est environ 0,1 g. On souhaite préparer 500 mL de solution d'hydroxyde de sodium dont le pH vaut 11,4 à 15°C. Produit ionique de l'eau à 15°C K_e= 2 10^-15.
   Calculer le nombre de pastilles de soude nécessaires.(12 ; 23 ; 29 ; 31 ; 45 ; aucune bonne réponse) [H₃O⁺][HO^-]=2 10^-15 ; [H₃O⁺] = 10^-11,4 = 4 10^-12 mol/L ;
   [HO^-] = 2 10^-15 / 4 10^-12 = 5 10^-4 mol/L
   masse de soude dans 0,5 L : 0,5*40*5 10^-4 = 0,01 g ( moins d'une pastille)

    

4. L'éthanoate de butyle est obtenu par chauffage à reflux pendant 1 heure d'un mélange de 60 mL d'acide éthanoïque et de 40 mL de butan-1-ol en présence de 2mL d'acide sulfurique concentré et de quelques grians de pierre ponce. Après séparation et purification on obtient 27 g d'éthanoate de butyle.
   Données : masse volumique butan-1-ol : 800 kg/m3 ; masse volumique acide acétique 1050 kg/m3
   masse molaire (g/mol) : acide acétique 60 ; butan-1-ol 74 ; éthanoate de buthyle 116.
   Combien d'affirmations sont exactes ?
   a- L'acide sulfurique joue le rôle de catalyseur.
   b- On chauffe le mélange pour améliorer le rendement
   c- La pierre ponce permet d'absorber l'eau au fur et à mesure de sa formation.
   d- L'acide éthanoïque est le réactif limitant.
   e- le rendement est d'environ 54% b: fausse " pour atteindre plus rapidement l'équilibre"
   c: fausse " régularise le chauffage"
   d: fausse : alcool : 40*0,8 = 32 g ; 32/ 74 = 0,432 mol
   acide éthanoïque : 60*1,05 = 63g ; 63/60 = 1,05 mol ( en excès)
   Qté de matière théorique d'ester : 0,432 mol ou 0,432*116 = 50,16 g
   rendement 100*27/50,16 = 54%

    

5. L'aspirine est préparée par action d'anhydride éthanoïque sur l'acide salycilique
   CH₃-CO-O-CO-CH₃ + HO-C₆H₄-COOH = CH₃-COO-C₆H₄-COOH + CH₃-COOH
   On introduit dans un erlenmeyer 7 g d'acide salycilique (M=138 g/mol) et 12 mL d'anhydride éthanoïque ( M=102 g/mol ; densité 1,08 ). Le rendement de la réaction est 63%
   Calculer la masse d'aspirine obtenue ( M= 180 g/mol) ( 5,75 ; 6,42 ; 6,83 ; 7,84 ; 9,13 ; aucune bonne réponse)

On effectue l'électrolyse de 200 mL d'une solution acidifiée de nitrate d'argent de concentration C=0,05 mol/L. On réalise cette électrolyse entre deux électrodes de graphite. L'argent se dépose à la cathode et du dioxygène se dégage à l'anode. L'électrolyse à durer 20 min avec un courant constant d'intensité I= 612 mA. La température du laboratoire est 17° et la pression de 1013 hPa.
couple oxydant /réducteur Ag⁺/Ag ; O₂/H₂O. N_A= 6,02 10²³ mol^-1 ; e= 1,6 10^-19 C ; R= 8,31 J mol^-1K^-1.

1. Déterminer la masse d'argent déposée à la cathode.
2. En déduire la concentration finale ( en mmol/L) en ion argent dans la solution.
3. calculer le volume ( en mL) de dioxygène dégagé au cours de l'électrolyse.

30 mL d'une solution d'acide chlorhydrique à 0,02 mol/L

10 mL de solution d'hydroxyde de sodium à 0,01 mol/L.
La transformation chimique est totale

ion	Na+	Cl-	H3O+	HO-
l Sm²mol-1	5,01 10-3	7,63 10-3	34,98 10-3	19,86 10-3

1. Ecrire l'équation de la réaction chimique entre l'acide chlorhydrique et l'hydroxyde de sodium
2. Calculer la concentration en ion oxonium ( en mmol/L) dans l'état final
3. Déterminer la conductivité s du mélange à l'état final. s = S l _i[X_i]