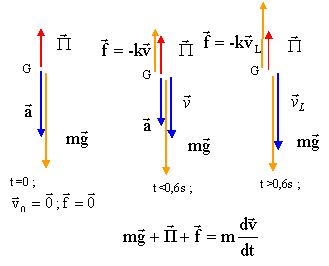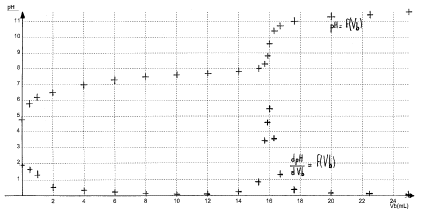
solution d’acide hypochloreux. ( 6,25 points )

On dispose d’un flacon d’une solution aqueuse S d’acide hypochloreux HClO dont l’étiquette indique une concentration molaire apportée C_A que l’on cherche. Données : teintes et zone de virage du rouge de crésol : jaune 7,2 – 8,8 rouge ; pK_Adu couple HClO(aq) / ClO^-(aq) : pKa = 7,25 ;

Le pH de la solution S est : pH = 4,8.

1. Sur un axe gradué en pH, placer les domaines de prédominance des espèces acide et basique du couple étudié.
2. On désire vérifier la valeur de la concentration C_A de l’acide hypochloreux indiquée sur l’étiquette. On dose un volume V_A= 20,0 mL de solution S par des ions hydroxyde contenus dans une solution de soude (hydroxyde de sodium) de concentration C_B= 0,01mol.L^-1. Écrire l’équation de la réaction de l’acide hypochloreux avec l’ion hydroxyde.
3. La courbe ci-dessous représente les fonctions pH = f (V_B) et dpH / dV_B= f ’(V_B). Expliquer comment l’on détermine le volume équivalent V_BEen se servant de cette courbe.
4. Quelle est la valeur de V_BE?
5. Définir l’équivalence.
6. Construire un tableau d’évolution associé à la transformation totale étudiée.
7. En déduire la valeur de la concentration molaire apportée C_A en acide hypochloreux de la solution étudiée.
8. Le dosage aurait pu être réalisé en utilisant un indicateur coloré acido-basique. Le rouge de crésol aurait-il pu être utilisé pour le dosage de cette solution S ? Justifier la réponse.

---

corrigé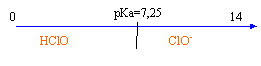

---

à pH=pKa la forme acide HClO et la forme base conjuguée ClO^- sont en quantité égale.

HClO+HO^- = ClO^- + H₂O

à l'équivalence du dosage acide base la courbe dérivée présente un maximum ; v_BE= 16 mL

à l'équivalence les réactifs mis en présence sont en quantité stoechiomètrique : avant l'équivalence l'un des réactifs est en excès ; après l'équivalence l'autre réactif est en excès.

	HClO	+HO- ajouté	= ClO-	+ H2O
initial	VACA= 0,02 CA mol	0	0	solvant
en cours	0,02 CA -x	x= CBVB	x= CBVB
équivalence	0,02 CA -xéq =0	xéq =CBVBE	xéq =CBVBE

x_éq =C_BV_BE = 0,016*0,01 = 1,6 10^-4 mol

0,02 C_A=x_éq = 1,6 10^-4 d'où C_A= 8 10^-3 mol/L.

La zone de virage de l'indicateur coloré doit contenir le pH du point équivalent ( voisin de 9 dans ce cas)

le rouge de crésol ne convient pas, la phénolphtaléine conviendrait mieux.

---

---

fonctionnement d’une pile. ( 9,5 points )

Données : un faraday est la valeur absolue de la charge électrique d’une mole d’électrons. 1 Faraday = 1F = 96500 C.mol ^-1.

On réalise une pile composée des deux demi-piles suivantes : - une lame de cuivre Cu plongeant dans 100 mL de solution aqueuse de sulfate de cuivre (Cu²⁺ (aq) + SO₄^2-(aq)) de concentration molaire apportée C₁= 0,50 mol.L^-1 ; - une lame d’argent Ag plongeant dans 100 mL de solution aqueuse de nitrate d’argent (Ag⁺(aq) + NO₃^-(aq)) de concentration molaire apportée C₂= 0,10 mol.L^-1 ; - les deux demi-piles sont reliées par un pont salin de nitrate de potassium. La pile est branchée aux bornes d’un conducteur ohmique. Un ampèremètre indique que le courant circule de l’électrode d’argent vers l’électrode de cuivre.

1. Faire un schéma de la pile en précisant : a. la polarité des électrodes ; b. le sens du courant ; c. le sens de circulation des électrons. d. Donner son schéma conventionnel.
2. Écrire les équations des réactions qui se produisent aux électrodes et donner l’équation globale de fonctionnement de la pile, en utilisant des nombres stoechiométriques entiers les plus petits possibles.
3. Calculer la valeur du quotient de réaction initial associé à l’équation précédente.
4. La constante d’équilibre associée à cette réaction est K = 2,1.10¹⁵. Le sens d’évolution du système satisfait-il aux critères d’évolution spontanée ?
5. La concentration molaire effective en ions métalliques de chaque demi-pile varie-t-elle ? Si oui, dans quel sens ?
6. Comment est assurée l’électroneutralité de chaque solution au cours du fonctionnement de la pile ?
7. Lorsque la pile cesse de fonctionner on peut considérer que tous les ions argent (I) ont été consommés. Calculer la quantité d’électricité maximale que peut fournir cette pile.
8. L’intensité mesurée par l’ampèremètre a pour valeur I = 2 mA. Pendant combien de temps la pile peut-elle fonctionner dans ces conditions ?
9. Déterminer, à l’aide d’un tableau d’avancement, la quantité d’ions cuivre (II) présents lorsque la pile cesse de fonctionner, et calculer leur concentration.

---

corrigé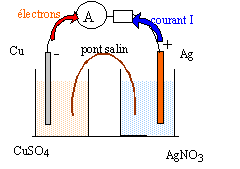

---

- Cu / Cu²⁺ //Ag⁺/Ag +

Cu = Cu²⁺ + 2e^- oxydation du cuivre

2Ag⁺ + 2e^- =2Ag réduction de Ag⁺.

2Ag⁺ +Cu=Cu²⁺ +2Ag

quotient de réaction initial Q_r,i =[Cu²⁺]/[Ag⁺]²=0,5 / 0,1² = 50.

Q_r,i < K donc évolution spontanée dans le sens direct.

[Cu²⁺] augmente et [Ag⁺] diminue.

à partir du pont salin, migration des ions nitrate dans le compartiment contenant le sulfate de cuivre et migration des ions potassium dans le compartiment contenant le nitrate d'argent afin que chaque solution reste électriquement neutre.

Qté de matière d'ion Ag⁺ au départ : 0,1*0,1 = 0,01 mol

donc 0,01 mol d'électrons sera mis en jeu.

La charge d'une mole d'électrons est 96500 C soit ici une quantité d'électricité égale à 96500*0,01 = 965 C.

durée de fonctionnement 965/ 210^-3 = 482 500 s = 134 heures.

	2Ag+	+Cu	=Cu2+	+2Ag
initial	0,01 mol	a	0,05 mol	b
en cours	0,01-2x	a-x	0,05+x	b+2x
fin	0,01-2xf=0	a-xf	0,05+xf	b+2xf

x_f= 0,005 mol et n_Cu2+ = 0,05+ 0,005 = 0,055 mol

[Cu²⁺]=0,055/0,1 = 0,55 mol/L.

---

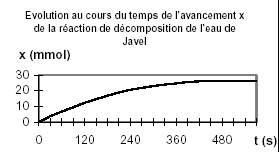
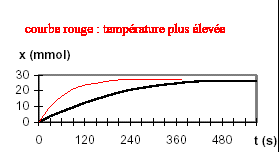
L’eau de Javel est une solution d’ions hypochlorite ClO^-(aq), d’ions chlorure Cl^-(aq), et d’ions sodium Na⁺(aq). On utilise une solution commerciale S₀ d’eau de Javel achetée en berlingot, dont le volume est V = 250 mL. L’eau de Javel se décompose lentement selon une transformation totale modélisée par la réaction d’équation :

2 ClO^-(aq) = 2 Cl^-(aq) + O₂(g) réaction (1)

Pour étudier la cinétique de la réaction (1) en présence d’un catalyseur, on dilue la solution commerciale S₀ afin d’obtenir un volume V₁= 100,0 mL d’une solution S₁ d’eau de Javel cinq fois moins concentrée. On déclenche un chronomètre au moment où l’on introduit le catalyseur dans le système chimique étudié. On mesure alors, à différentes dates, le volume de dioxygène V(O₂)_oo dégagé dans des conditions telles que le volume molaire soit : Vm = 22,4 L.mol^-1. A la fin de la transformation, le volume de dioxygène mesuré est V(O₂)_oo= 295 mL.

1. Construire un tableau d’évolution associé à la transformation totale étudiée ici.
2. Établir l’expression littérale de l’avancement x(t) de la transformation à chaque date t en fonction de V(O₂)t et Vm.
3. On note C₁, la concentration en ions hypochlorite [ClO^-]₀ à la date t = 0 s dans la solution S₁. Établir l’expression de C₁en fonction de V(O₂)_oo, V₁et Vm .
4. La courbe ci-dessous représente l’évolution de l’avancement x de la réaction au cours du temps. Donner l’expression de la vitesse volumique v de la réaction.
5. Comment cette vitesse volumique évolue-t-elle au cours du temps ? Justifier.
6. Tracer l’allure qu’aurait la courbe x = f (t) si la réaction était réalisée à une température plus élevée.

Oscillations dans un circuit LC idéal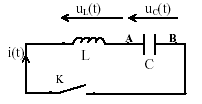

Le condensateur est initialement chargé sous une tension U₀. A un instant pris comme origine des dates, on ferme l'interupteur K et on suit l'évolution de la charge q(t) portée par l'armature A du condensateur. On néglige la résistance.

1. Exprimer les tensions u_C(t) et u_L(t) en fonction de q(t), L et C. Etablir l'équation différentielle vérifiée par q(t).
2. Montrer que la fonction q(t)=Q_m cos(w₀t) est solution de l'équation différentielle en identifiant w₀ et Q_m.
   Exprimer la période T₀ en fonction de Let C.
   - Pour U₀= 10V, C=2mF et L=0,02 H calculer w₀ et Q_m.
3. Quelle est la valeur de l'intensité du courant avant la fermeture de K ?
   - Donner l'expression littérale de l'intensité du courant. Exprimer puis calculer la valeur maximale de l'intensité I_max.
   - Comment est modifiée l'amplitude de l'intensité par la présence d'une résistance dans le circuit ?

datation d'une roche :

La méthode potasium-argon permet de dater les roches dont la teneur en potassium est significativ dans une gamme d'âges de trois milliards d'années àquelques dizaines de milliers d'années. Les roches volcaniques contiennent l'isotope 40 du potassium ; ce dernier est radioactif et se désintègre en argon 40 avec une demi-vie ou période t½= 1,4 10⁹ ans. L'agon est un gaz qui est en général retenu par la roche.

Lors d'une éruption la roche perd le'argon 40 : c'est le dégazage. A la date de l'éruption la lave ne contient donc plus d'argon. Au cours du temps l'argon 40 s'accumule à nouveau dans la roche alors que le potassium 40 disparaît peu à peu. On considère les masses des atomes de potassium 40 et d'argon 40 identiques.

1. Qu'appelle-t-on isotopes ? ⁴⁰₁₉K Que signifie les nombres 19 et 40 ? Quelle est la composition du noyau de potassium 40 ? Quel nombre caractérise l'élément chimique ?
2. L'analyse d'un échantillon de basalte montre qu'il contient m=1,4 mg de potassium 40 et une masse m'=0,2 mg d'argon 40. On prend l'origine des dates au moment de l'éruption volcanique.
   - Ecrire l'équation de désintégration du potassium 40 en argon 40 ( Z=18).
   - Quelle était la masse m₀ de potassium 40 à la date de l'éruption ? Justifier.
   - Exprimer le nombre de noyaux de potassium 40, noté N en fonction de la constante radioactive, du temps et du nombre de noyaux initiaux noté N₀.
   - Etablir l'expression entre la constante radioactive et la demi-vie . Exprimer N(t) en fonction de N₀ et t½.
   - Exprimer l'âge de la roche en fonction de m₀, m et t½. Faire le calcul.

Chute verticale d'une bille :

Une petite bille de masse m, de rayon r est totalement immergée dans un liquide de masse volumique r ; elle est abandonnée d'un point O, sans vitesse initiale à l'instant t=0.

L'axe z est vertical, orienté vers le bas; son origine est O.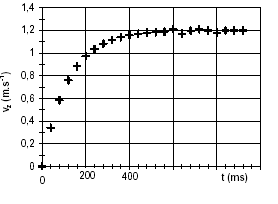

1. Déterminer graphiquement la vitesse limite de chute et le temps caractéristique noté t. Expliquer la démache.
   - Donner la relation entre la vitesse et l'accélération du centre d'inertie G de la bille à une date t.
   - Comment obtenir graphiquement la valeur de l'accélération à une date t. Comment évolue la valeur de l'accélération au cours de la chute ? Justifier.
   - Calculer l'accélération initiale.
2. Pendant la chute la bille est soumise à une force de frottement fluide de valeur f = kv , colinéaire à la vitesse et de sens contraire.
   - Donner les caractéristiques de la poussée d'Archimède notée P.
   - Quelle relation les forces exercée sur la bille vérifient-elles ? Faire des schémas représentant ces forces ainsi que le vecteur vitesse et accélération du point G à trois instants différents : à t=0 , pendant le régime initial puis pendant le régime asymptotique.
   - Etablir l'équation différentielle du mouvement en faisant intervenir la vitesse v. Montrer qu'elle peut s'exprimer sous la forme dv/dt= A-Bv. Identifier A et B et donner leurs unités.
   - Exprimer la vitesse limite en fonction de A et B.
   - Donner les valeurs numériques de A et B.
   - Montrer que la fonction v= C(1-e ^-bt) est solution de l'équation différentielle et identifier les constantes C et b. Exprimer C et b en fonction de A et B. Que représente physiquement la constante C.
3. On suppose que l'exprérience précédente est réalisée dans un long tube où règne le vide. Les repères d'espace et de temps restent les mêmes.
   - La bille atteindra-t-elle une vitesse limite ? Justifier.
   - Exprimer la vitesse au cours de cette chute et établir l'équation horaire du mouvement de la bille.

---

corrigé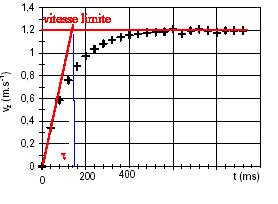

---

l'asymptote horizontale donne la vitesse limite v_L=1,2 m/s.

l'intersection de la tangente à l'origine avec l'asymptote donne le temps caractéristique t = 140 ms = 0,14 s.

le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps; ces deux vecteurs sont portés par la verticale. La relation entre les valeurs algébriques est a= dv/dt ; la vitesse a le sens du mouvement ; la valeur de la vitesse augmente jusqu' à 1,2 m/s ; la variation de la vitesse est positive, donc l'accélération a le sens du mouvement.

Graphiquement , la valeur de l'accélération est égale au coefficient directeur de la tangente à la courbe à la date t.

cette valeur diminue, la tangente à la courbe se rapproche de l'horizontale lorsque le temps augmente.

lorsque la vitesse limite est atteinte, l'accélération est nulle et le mouvement est rectiligne uniforme.

à t=0 on trouve : a=1,2/ 0,14 = 8,6 m/s².

---

la poussée d'Archimède est appliquée au centre du volume de liquide déplacé, dirigée suivant la verticale ascendante ; sa valeur est égale au poids du volume (V en m³) de liquide déplacé P=rgV avec V= 4/3pr³.

Au cours de la chute la somme vectorielle des forces appliquées à la bille est égale au produit de la masse de la bille (kg) par l'accélération du centre d'inertie de la bille (seconde loi de Newton).

projection sur un axe vertical vers le bas : mg - rg4/3pr³ -kv = mdv/dt

dv/dt = g(1- r/r_bille) -k/mv

A= g(1- r/r_bille) exprimé en m/s² ; B= k/m exprimé en s^-1.

lorsque la vitesse limite est atteinte dv/dt = 0 et A-Bv_L=0 soit v_L= A/B= 1,2 ou A= 1,2 B.

à t=0 ; [dv/dt]_t=0 = A car la vitesse initiale est nulle A= 8,6 m/s² ( question 1) et B= 7,16 s^-1.

---

v= C(1-e ^-bt)

dérivée par rapport au temps: dv/dt = bCe ^-bt

repport dans dv/dt = A-Bv : bCe ^-bt = A-BC(1-e ^-bt) = A-BC+BCe ^-b.

d'où A-BC=0 soit C= A/B exprimé en m/s ( il s'agit de la vitesse limite de chute)

bC = BC soit b=B , inverse du temps caractéristique.

Dans le cas d'une chute libre dans le vide:

- il n'y a pas de vitesse limite de chute, la bille n'est soumise qu'à son poids

l'accélération est g=9,8 m/s² au niveau du sol terrestre

vitesse = g t et hauteur de chute = ½ g t².

---