|
Physique - Chimie
services
de santé des armées d'après concours 2004
ondes - oscillations
mécaniques - projectile- radioactivité - acide
base - conductivité, cinétique, pile
|
|
|
|
Ondes (4 points)
- Ondes mécaniques
Un vibreur est le siège d’un mouvement vibratoire périodique de
fréquence f = 100 Hz. Les vibrations qu’il crée se propagent le long
d’une corde élastique, à partir de son extrémité S, avec la célérité v
= 8,0 m.s–1.
- Exprimer littéralement puis calculer la longueur d’onde l de l’onde qui se propage le long de la corde.
- Comparer le mouvement d’un point A situé à 16 cm du point S à celui
d’un point B situé à 40 cm de S. Justifier.
- 2. Ondes sonores
Les chauves-souris sont capables de repérer leurs proies grâce aux
ondes ultrasonores. Elles émettent des ultrasons et l’analyse de l’écho
renvoyé par les proies permet de localiser celles-ci. On suppose qu’une
chauve-souris veuille repérer un insecte situé à une distance d = 3,5 m
d’elle. La chauve-souris et l’insecte sont immobiles dans le
référentiel terrestre. La vitesse de propagation des ondes ultrasonores
dans l’air est v = 350 m.s–1. Le milieu ambiant est supposé
homogène et non dispersif.
- Définir un milieu non dispersif.
- Quelle doit-être la durée maximale de l’émission pour que le front de
l’onde réfléchie ne se superpose pas à l’onde émise ?
- 3. Ondes lumineuses
La lumière monochromatique issue d’un laser est diffractée par une
fente fine verticale de largeur a. La figure de diffraction est
observée sur un écran situé à la distance D de la fente. La largeur de
la tache centrale a pour valeur 2d. On appelle écart angulaire l’angle q entre le milieu de la tache centrale et la
première extinction.
- Faire une figure claire, dans le plan horizontal contenant le
faisceau laser et la figure de diffraction, en y indiquant les
grandeurs d, D et q.
- L’écran est situé loin de la fente et l’écart angulaire est petit :
on peut faire l’approximation q =tan q. ( q étant exprimé
en radians). En déduire l’expression de q
en fonction de d et D.
- L’écart angulaire q dépend de la longueur
d’onde l de la radiation utilisée ainsi que
de la largeur de la fente. Donner l’expression littérale correspondante.
- En déduire l’expression littérale de la longueur d’onde l en fonction de d, D et a.
- Calculer la longueur d’onde l sachant que
a = 0,10 mm, D = 2,0 m et d = 2,0 cm.
corrigé
longueur d'onde l =v /f = 8/100 = 0,08 m.
mouvement d’un point A situé à 16 cm (soit 2l)
du point S : A et S sont distants d'un nombre entier de longuer d'onde
: ils vibrent en phase
mouvement d’un point B situé à 40 cm ( soit 4,5 l ) de S : A et B sont distants d'un nombre
impair de demi longueur d'onde : ils vibrent en opposition de phase
Dans un milieu non dispersif la célérité des ondes est
indépendante de la fréquence des ondes.
durée maximale de l’émission pour que le front de l’onde
réfléchie ne se superpose pas à l’onde émise :
l'émission doit cesser dès que le front de l'onde réfléchie
atteint le récepteur ( la chauve souris) ; onde incidente et réfléchie
ont parcouru 2d=7 m à la célérité de 350 m/s.
t= d/v= 7 / 350 = 0,02 s.
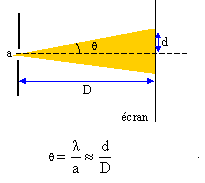
l= ad/D avec a= 10-4 m ;
d= 0,01 m et D= 2m
l= 10-4* 10-2/2
= 0,5 10-6 m = 500 nm.
|
|
(6 points)
Un pendule élastique est constitué d’un mobile de masse m =
100 g pouvant se déplacer sur un banc à coussin d’air horizontal. Ce
mobile est attaché à un point fixe par un ressort à spires non
jointives de raideur k = 10 N.m–1. À l’équilibre, la
position du centre d’inertie du mobile coïncide avec le point O,
origine du repère (O ; i ). On écarte le solide de sa position
d’équilibre et on le lance avec une vitesse v0 à un instant
pris comme origine des dates.

Le référentiel terrestre est considéré comme galiléen pendant
la durée de l’étude. Les frottements exercés par l’air peuvent être
modélisés par une force f colinéaire et de sens opposé au vecteur
vitesse v du centre d’inertie G du mobile telle que la valeur de f soit
f=mv
- Exprimer la coordonnée Fx de la force F exercée
par le ressort sur le solide en fonction de l’abscisse x du centre
d’inertie G.
- Exprimer la coordonnée fx de la force de
frottement f en fonction de la coordonnée vx du vecteur
vitesse v .
- Faire le bilan des forces appliquées au solide lors de son
mouvement (t = 0). Représenter ces forces, sans souci d’échelle, sur
deux schémas différents numérotés, (dans chacun des cas, le mobile sera
représenté dans la position qu’il occupe sur le schéma ci-dessus à
l’instant de date t1 :
- schéma n°1 : lorsque le mobile s’éloigne de sa position d’équilibre ;
- schéma n°2 : lorsque le mobile s’approche de sa position d’équilibre.
- En appliquant la deuxième loi de Newton, établir l’équation
différentielle vérifiée par l’abscisse x du centre d’inertie G du
mobile.
- On suppose maintenant que les frottements exercés par l’air
sont négligeables. Dans ce cas, l’équation différentielle du mouvement
admet une solution de la forme x = Xm cos (2p t/T0+j0)
- Donner l’expression littérale de la période propre T0 en
fonction des grandeurs caractéristiques de l’oscillateur. Calculer T0.
- Calculer les valeurs de Xm et de j0
sachant que : x(t = 0) = x0 = + 2,0 cm et vx(t =
0) = v0x = – 0,20 m.s–1.
corrigé
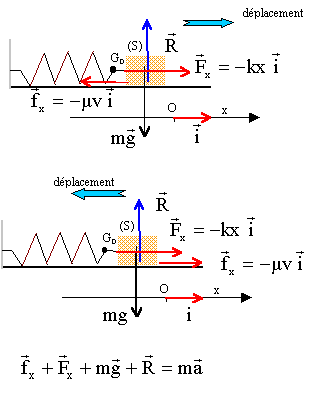
projection sur
l'axe horizontal : ( attention l'abscisse x est négative , solide à
gauche de O) Fx = -kx
déplacement à
droite, la vitesse a le sens de l'axe v>0 et fx = -mv: -kx -mv =
mx" avec v= dx/dt = x'
mx" +mx'+kx =0
déplacement à
gauche, la vitesse a le sens contraire de l'axe v <0 et fx
= -mv : -kx -mv = mx" avec v= dx/dt = x'
mx" +mx'+kx =0.
x = Xm cos (2p t/T0+j0)
période T0 = 2p(m/k)½=
2*3,14(0,1/10)½ = 6,28 * 0,1 = 0,628
s.
l'énergie mécanique au moment du lâcher
à t=0 est à la fois sous forme potentielle élastique et sous forme
cinétique :
E=½kx²0 + ½mv²0 =
0,5*10*0,02²+0,5*0,1*0,2² = 4 10-3 J
lorsque la vitesse est nulle, l'énergie
mécanique est sous forme potentielle élastique ½kX²m avec Xm,
l'amplitude en mètre.
l'énergie mécanique se conserve (
absence de frottement) 4 10-3 = ½kX²m
Xm = (8 10-3 / 10)½
= 2,8 10-2 m = 2,8 cm.
phase à t=0 :
x(t=0) = 0,02 = 0,028 cos j0
soit cos j0 = 2/2,8 = 0,714 soit
j0 =0,77 rad ou bien j0 = -0,77 rad
vitesse , dériver x(t) par rapport au temps : x' = v = -Xm2p /T0 sin (2p
t/T0+j0)
vitesse à t=0 : -0,2 m/s soit 0,2 = Xm2p /T0 sin j0
;
Xm2p /T0 étant
positif alors sin j0
doit être positif et en conséquence j0
= 0,77 rad.
|
|
mouvement d'un projectile (4
points)
Un jongleur lance une balle d’un point O, verticalement vers
le haut, avec une vitesse v0 . Le centre d’inertie G de la
balle s’élève verticalement jusqu’au point A, situé à une hauteur h au
dessus du point O, avant de redescendre. La balle, de masse m, est
considérée comme ponctuelle et en mouvement de chute libre. Dans le
référentiel terrestre, considéré comme galiléen pendant la durée de
l’étude, on choisit un axe (Oy) vertical et ascendant, ayant pour
origine le point O de lancement. L’instant du lancement de la balle est
choisi comme instant origine des dates. On note g la valeur du champ de
pesanteur.
- Établir l’équation différentielle vérifiée par la
coordonnée vy du vecteur vitesse v de la balle.
- Résoudre analytiquement cette équation.
- En déduire que le mouvement de la balle comporte bien une
phase de montée et une phase de descente. Exprimer la date t1
du changement de phase en fonction de v0, valeur de la
vitesse initiale, et de g.
- Déterminer l’équation horaire y = f(t) du mouvement de la
balle.
- Exprimer la valeur v0 de la vitesse en fonction
de h et g.
corrigé
la chute étant libre, la balle n'est soumise
qu'à son poids, vertical, orienté vers le bas
la seconde loi de
Newton conduit à accélération a, verticale, orientée vers le bas, de
valeur g.
la vitesse est
une primitive de l'accélération : vy= -gt +v0.
la vitesse
initiale vaut v0, puis la vitesse diminue durant la montée;
la vitesse s'annule à t1=v0/g puis la balle redescend et la vitesse crôit
jusqu'à la valeur v0, atteinte juste avant de toucher le sol.
la position de la
balle est une primitive de la vitesse :y(t) = -½gt²+v0t.
à la date t1=v0/g : y(t1)=h
h= -½g(v0/g)2+v0v0/g =½v0²
/g soit v0²
= 2gh.
|
|
réactions nucléaires (6
points)
Données : iode I ( Z=53) ; xénon Xe (Z=54) ; césium Cs (Z= 55)
; baryum Ba (Z= 56) ; lanthane La (Z=57)
La masse du noyau d’un élément X sera notée mX . mp
= masse du proton ; mn = masse du neutron
Un réacteur de centrale nucléaire fonctionne à l’uranium
enrichi (3% d’uranium 235 fissile et 97% d’uranium 238 non fissile).
- Le noyau d’uranium 235
- Donner la composition du noyau d’uranium 23592
U.
- Donner l’expression du défaut de masse |Dm|
de ce noyau en utilisant les notations définies précédemment.
- Donner l’expression de l’énergie de liaison du noyau d’uranium 23592
U. Préciser les unités.
- Fission de l’uranium 235
Par capture d’un neutron lent, un noyau d’uranium 235 subit une
réaction de fission d’équation :
23592 U + 10n
-->x54 Xe + 94y Sr + 310n
- Calculer les valeurs de x et de y en précisant les lois de
conservation utilisées.
- Donner l’expression de l’énergie libérée par la fission d’un noyau
d’uranium 23592 U en utilisant les notations
définies précédemment.
- Désintégration du noyau de césium 137
Les produits de fission sont radioactifs et se transmutent en d’autres
produits, eux-mêmes radioactifs. Parmi ces déchets, on trouve le césium
137, radioactif ß–, dont la demi-vie t1/2 = 30
ans.
- Écrire l’équation de la désintégration d’un noyau de césium 137, le
noyau fils étant formé dans un état excité.
- Quelle est la nature du rayonnement émis lors de la désexcitation du
noyau fils ?
- Définir la demi-vie d’un noyau radioactif.
- À un instant choisi comme origine des dates, on dispose d’un
échantillon de césium 137 de masse m0. Donner l’expression
littérale de la masse m de césium 137 restant à l’instant de date t en
fonction de m0 et de t1/2 .
- Montrer qu’à la date t = n t1/2, la fraction de la masse
initiale restante vaut : m/m0 = 1/ 2n.
- En déduire la durée approximative au bout de laquelle la masse
restante de césium 137 est égale à 0,1% de sa masse initiale.
corrigé
omposition du noyau d’uranium 23592
U : 92 protons et 235-92 =143 neutrons.
défaut de masse |Dm| = |masse des
neutrons et protons isolés et au repos - masse du noyau|
|Dm| =|92 mp+143 mn-
mU|
énergie de liaison du noyau d’uranium 23592
U , énergie qu'il faut fournir au noyau pris au repos pour le dissocier
en ses nucléons : |Dm| c², exprimée en joule.
23592 U + 10n
-->x54 Xe + 94y Sr + 310n
conservation de la charge : 92 = 54 + y soit y =38.
conservation du nombre de nucléons : 235+1 = x + 94 + 3 soit x
=139.
expression de l’énergie libérée par la fission d’un noyau
d’uranium 23592 U :
|Dm| =|mXe + mSr
+ 2mn-mU| ; E=|Dm| c².
désintégration d’un noyau de césium 137
13755 Cs-->13756
Ba* + 0-1e suivi de :13756
Ba* -->13756 Ba +00g.
le noyau de baryum excité libére de l'énergie sous forme d'un
photon g en revenant à l'état fondamental.
la demi-vie d’un noyau radioactif est la durée au bout de
laquelle la moitié des noyaux initiaux se sont désintégrés.
m(t) = m0 exp(-lt) avec lt½ = ln2
ln( m/m0) = -l t = -t /
t½ ln2
on pose n =t / t½ d'où ln( m/m0) = -n
ln2 = ln2-n ; soit m/m0 =2-n ; m/m0 = 1 /2n.
durée approximative au bout de laquelle la masse restante de
césium 137 est égale à 0,1% de sa masse initiale :
m= 10-3 m0 ; m/m0= 10-3
; 10-3 = 2-n soit ln 10-3 = - n ln2 ;
n = ln1000 / ln 2 =6,9 / 0,69 = 10
la durée est voisine de 10 demi-vie. t
= 10 t½.
|
|
étude de deux acides (9
points)
On se propose de comparer, à partir de mesures pH-métriques,
le comportement de deux acides : l’acide nitreux (HNO2 ) et
l’acide hypochloreux (HOCl).
- Étude théorique préliminaire :
On dispose d’un volume V d’une solution aqueuse d’un acide HA de
concentration molaire en soluté apporté c. La transformation mettant en
jeu la réaction de l’acide HA avec l’eau n’est pas totale.
- Écrire l’équation de la réaction de HA avec l’eau.
- Dresser le tableau descriptif de l’évolution du système chimique en
utilisant les grandeurs V, c et xéq , avancement dans l’état
d’équilibre du système chimique.
- Exprimer les concentrations molaires effectives des espèces chimiques
présentes dans l’état d’équilibre en fonction de c et de la
concentration molaire effective en ions oxonium à l’équilibre [H3O+]éq.
- En déduire l’expression du quotient de réaction dans l’état
d’équilibre Qr,éq en fonction de [H3O+]éq
et de la concentration molaire c.
- Exprimer, en fonction de [H3O+]éq et
de c, le taux d’avancement dans l’état d’équilibre.
- Préparation d’une solution de concentration déterminée :
On dispose du matériel suivant :
• Béchers de 50 mL, 100 mL et 250 mL.
• Éprouvettes graduées de 10 mL, 20 mL, 50 mL et 100 mL.
• Fioles jaugées de 50 mL, 100 mL et 250 mL, volume délivré à 0,1 %
près.
• Pipette graduée de 10 mL à ± 0,1 mL.
• Pipette jaugée de 10 mL à ± 0,05 mL.
• Poire à pipeter.
On veut préparer une solution S de l’acide HA de concentration molaire
en soluté apporté c = 1,00 × 10-3 mol.L-1 à
partir d’une solution mère S0 de concentration molaire en
soluté apporté c0 = 1,00 × 10-2 mol.L-1.
- Quelle est la verrerie à utiliser ? Justifier.
- Décrire le protocole.
- Étude expérimentale :
On a effectué un ensemble de mesures de pH pour des solutions d’acide
nitreux et d’acide hypochloreux de diverses concentrations molaires en
soluté apporté à une température de 25°C. Le tableau ci-dessous donne
les valeurs moyennes des résultats des mesures et une partie de leur
exploitation.
|
c (mol/L)
|
pH
|
[H3O+]éq
|
Qr, éq
|
-log Qr, éq
|
|
acide nitreux
|
0,001
|
3,3
|
5 10-4
|
5 10-4
|
3,3
|
|
0,005
|
2,87
|
1,4 10-3
|
5 10-4
|
3,3
|
|
0,01
|
2,7
|
|
|
|
|
acide hypochloreux
|
0,001
|
5,15
|
7,1 10-6
|
5 10-8
|
7,3
|
|
0,005
|
4,8
|
1,6 10-5
|
5 10-8
|
7,3
|
|
0,01
|
4,65
|
2,2 10-5
|
5 10-8
|
7,3
|
-Calculer les valeurs manquantes du tableau : présenter les calculs
sous forme littérale avant d’effectuer les applications numériques.
- Calculer, pour une même concentration molaire en soluté apporté c =
1,00 × 10–3 mol.L-1, les valeurs des taux
d’avancement, dans l’état d’équilibre, de la réaction de chaque acide
avec l’eau.
- Comparer le comportement des deux acides en solution aqueuse.
- Donner la définition de la constante d’acidité KA d’un
couple acide/base et en déduire son expression.
- Expliquer comment les résultats de cette étude expérimentale
permettent de trouver les valeurs respectives des pKA des
deux couples.
corrigé
HA + H2O = A- + H3O+.
|
HA
|
+ H2O
|
= A-
|
+ H3O+
|
|
initial
|
Cv
|
solvant, très grande quantité
|
0
|
0
|
|
en cours
|
Cv-x
|
x
|
x
|
|
équilibre( fin)
|
Cv-xéq
|
xéq
|
xéq
|
[A- ]éq=[ H3O+]éq=
xéq
/ v ; [HA]éq=C-xéq / v = C-[ H3O+]éq
quotient de réaction dans l’état d’équilibre Qr,éq
= [A- ]éq[
H3O+]éq/[HA]éq
Qr,éq = [ H3O+]éq2/[HA]éq=[
H3O+]éq2/ (C-[ H3O+]éq)
taux d'avancement
final : t = xéq/xmax
= xéq/Cv =[
H3O+]éq/C.
Le facteur de dilution est de 10 ( rapport des
concentrations)
le volume de la
pipette graduée doit être 10 fois plus petit que celui de la fiole
jaugée
prélever 10 mL de
la solution mère S0 à l'aide d'une pipette graduée.
placer dans un
fiole jaugée de 100 mL et compléter jusqu'au trait de jauge à l'aide
d'eau distillée. Homogénéiser.
[H3O+]éq = 10-pH = 10-2,7
= 2 10-3
mol/L.
Qr,éq = [ H3O+]éq2/
(C-[ H3O+]éq) = (2 10-3)2
/ (0,01-2 10-3) = 4 10-6 / 8 10-3 = 5 10-4 .
-log Qr,éq
= - log (5 10-4)
= 3,3.
valeurs des taux d’avancement, dans l’état d’équilibre, de la
réaction de chaque acide avec l’eau : [ H3O+]éq/C.
acide nitreux : 5 10-4 / 10-3 = 0,5.
acide hypochloreux : 7,1 10-6 / 10-3 = 7,1 10-3.
l'acide nitreux est beaucoup plus dissocié que l'acide
hypochloreux.
la réaction de l'acide nitreux avec l'eau est très avancée
alors que l'acide hypochloreux ne réagit pratiquement pas avec l'eau.
constante d’acidité KA d’un couple acide/base : Ka
= Qr, éq =[A-
]éq[ H3O+]éq/[HA]éq
pKa = -log Qr, éq
la dernière colonne du tableau donne les valeurs des pKa,
valeurs qui ne dépendent que de la température et non pas de la
concentration apportée en acide.
|
|
Cette partie comporte trois exercices. Chaque exercice
comporte des affirmations indépendantes .Toute réponse doit être
accompagnée de justifications ou de commentaires. A chaque affirmation,
vous répondrez donc par VRAI ou FAUX, en justifiant à l’aide de
définitions, de tableau d’avancement, de calculs, d’équations…
- Conductimétrie : on
prépare un volume V = 1,0 L de solution d’acide fluorhydrique par
dissolution d’une quantité de matière n = 1,0 × 10-3 mol de
fluorure d’hydrogène HF dans l’eau. On mesure, à 25°C, la conductivité
de la solution. La valeur obtenue est s=
22,3 × 10-3 S.m-1
Données : conductivités molaires ioniques à 25°C en S.m2
.mol-1: lH3O+ = 35 × 10-3
; l F- = 5,5 × 10-3
- La transformation chimique est modélisée par
l’équation de la réaction suivante :
HF(aq) + H2O(l) = H2F+(aq) + OH-(aq)
- L’avancement final de la réaction est xf = 0,55 mmol.
- La constante de la réaction a pour expression KA = x²f
/ ((n-xf)²V)
- La valeur de la constante de réaction est KA = 0,68
- Cinétique de réaction :
on suit par spectrophotométrie la cinétique de la réaction des ions
iodure avec les ions peroxodisulfate qui conduit à la formation du
diiode et d’ions sulfate. L’équation de la réaction est la suivante :
S2O82-(aq) + 2I-(aq) = I2
(aq) + 2 SO42-(aq)
Les concentrations molaires et les volumes des solutions réactives
introduites sont les suivants : [S2O82-]
= C1 = 0,50 mol/L ; V1 = 10,0 mL ; [ I-
] = C2 = 0,020 mol/L ; V2 = 10,0 mL
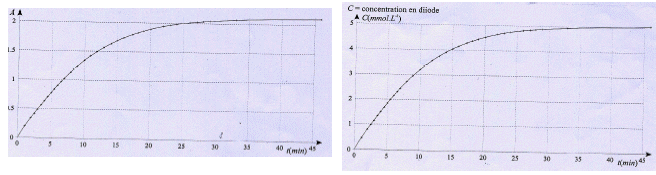
On a obtenu la courbe ci-dessous donnant l’absorbance A du système
chimique en fonction du temps t . On en a déduit la courbe donnant la
concentration molaire en diiode en fonction du temps.
Une solution de diiode jaune absorbe dans le bleu. Les
ions de la solution sont incolores.
- La longueur d’onde choisie pour le suivi spectrophotométrique
correspond à une radiation jaune.
- La loi de Beer-Lambert utilisée s’écrit A = e × l × [I2]
avec « l » épaisseur de la cuve, e le coefficient d’absorbance pour la
longueur d’onde choisie. La valeur de « e × l » pour cette cinétique
est environ égale à 0,42 L.mol-1.
- La transformation est totale.
- Etude de la pile Plomb/Zinc
: on réalise les demi-piles Zn2+(aq) / Zn(s) et Pb2+(aq)
/ Pb(s). Chaque demi-pile contient 100 mL de solution de concentration
molaire en ions Zn2+ et Pb2+ égale à 1,00 mol.L-1.
Les électrodes en Zinc et en Plomb sont en très large excès. On
considère la réaction Zn(s) + Pb2+(aq) = Zn2+(aq)
+ Pb(s) dont la constante d’équilibre a pour valeur K = 2 × 10+21
- La valeur du quotient de réaction dans l’état initial
est égale à 1.
- Le système évolue dans le sens inverse de la transformation
considérée.
- Lorsque l’équilibre est atteint, [Pb2+] = 0 mol.L-1.
- La lame de zinc constitue l’électrode positive de la pile.
- La lame de plomb est le siège d’une oxydation.
- La masse de plomb maximale formée est 0,207 g.
- La pile en fonctionnement est un système en équilibre.
Données : M (Zn ) = 65,4 g.mol-1 M ( Pb ) = 207
g.mol-1
corrigé
faux : l’équation de la réaction doit être :
HF + H2O = H3O+ + F-.
|
HF
|
+ H2O
|
= F-
|
+ H3O+
|
|
initial
|
Cv = 10-3 mol
|
solvant, très grande quantité
|
0
|
0
|
|
en cours
|
10-3 -x
|
x
|
x
|
|
équilibre( fin)
|
10-3 -xéq
|
xéq
|
xéq
|
s = lH3O+[ H3O+]éq
+l F-[F- ]éq=(lH3O++l F-)xéq / v =(lH3O++l F-) 103 xéq avec v= 1 L = 10-3 m3
xéq =s /(lH3O++l F-) = 22,3 /(35+5,5)10-3 = 0,55 mmol. exact.
[A- ]éq=[
H3O+]éq= xéq / v ; [HA]éq=(n-xéq )/ v
constante de réaction ou quotient de réaction dans l’état
d’équilibre Qr,éq = [A- ]éq[ H3O+]éq/[HA]éq
Qr,éq = x²f / ((n-xf)v) la
proposition est donc fausse.
valeur de la constante de réaction est KA =(0,55 10-3)2
/ ((1-0,55)10-3)= 0,68 10-3;
le volume est v= 1 L.
la valeur
proposée est donc fausse.
le diiode absorbe dans le bleu et transmet la
couleur complémentaire le jaune
on doit choisir
une radiation bleu pour laquelle l'absorption de la solution de diiode
est maximum. ( proposition fausse)
La loi de Beer-Lambert utilisée s’écrit A = e × l × [I2]
soit e × l = A / [I2]
à t supérieur à 40 minutes la concentration en diiode de varie
plus et vaut 5 10-3 mol/L tandis que l'absorbance est
voisine de 2,1.
e × l = A / [I2] = 2,1 / 5 10-3 = 420 L/mol ; la valeur proposée est donc fausse.
|
S2O82-(aq)
|
+ 2I-(aq)
|
= I2 (aq)
|
+ 2 SO42-(aq)
|
|
initial
|
C1V1= 5 10-3 mol
|
C2V2= 2 10-4 mol
|
0
|
0
|
|
en cours
|
5 10-3 -x
|
2 10-4 -2x
|
x
|
2x
|
|
fin
|
5 10-3 -xmax
|
2 10-4 -2xmax
|
xmax
|
2xmax
|
si le thiosulfate est en défaut : 5 10-3 -xmax =0 soit xmax = 5 10-3 mol
si l'ion iodure
est en défaut : 2 10-4 -2xmax =0 et xmax =10-4
mol , valeur à
retenir
on obtient au
plus, si la transformation est totale 10-4 mol de diiode
dans 20 mL
[ I2]fin = 10-4
/ 0,02 = 5 10-3 mol/L = 5 mmol/L ( valeur lue sur le graphe)
donc
transformation totale et la proposition est vraie.
Zn(s) + Pb2+(aq) = Zn2+(aq)
+ Pb(s)
Qr= [Zn2+] / [Pb2+] ; Qr
i= [Zn2+]i / [Pb2+]i
= 1 vrai.
Qr i< K donc évolution spontanée dans le sens
direct : la proposition est fausse.
les ions Pb2+ sont réduits et disparaissent de la
solution : la pile est usée quand ces ions Pb2+ ont tous
disparu.
[Pb2+] fin = 0 mol.L-1. vrai.
La lame de zinc s'oxyde Zn (s) =Zn2+ + 2e-
et constitue l'anode négative de la pile ; la proposition est fausse.
les ions Pb2+ sont réduits en plomb. La lame de plomb est le
siège d’une réduction ; la proposition est fausse.
La masse de plomb maximale formée est 0,1 mol soit 0,1*207 = 20,7 g ; la valeur proposée est fausse.
La pile en fonctionnement est un système hors équilibre ; la
proposition est fausse.
|
|
retour -menu
|



