Après l'installation d'un système de climatisation, on réalise une étude acoustique d'un bureau. On considère que le bruit engendré par le soufflage de l'air est assimilable à une source sonore. L'équipement aéraulique ne devra pas engendrer un niveau sonore global à l'intérieur du bureau supérieur à 35 dB_A. On mesure, par octave, la puissance acoustique de la source et le temps de réverbération au niveau du bureau.

fréquence (Hz)	125	250	500	1000	2000	4000
niveau de puissance Lw(dB)	35	42	41	39	36	36
niveau de réverbération T(s)	0,7	0,6	0,6	0,5	0,5	0,4

Données .- le volume du bureau est 30 m³.

- l'expression du niveau de pression acoustique dans le cas d'un local clos avec réverbération est L_p = L_w + 10 log(4/A)

L_p est le niveau de pression acoustique en un point en dB.

L_w est le niveau de puissance acoustique en dB.

A est l'aire d'absorption équivalente en m².

- on admet que la formule de Sabine est : T = 0,16 V/A

où T est la durée de réverbération en s et V est le volume du local en m³.

- les valeurs des pondérations acoustiques, par octave, exprimées en dB_A, sont :

fréquence (Hz)	125	250	500	1000	2000	4000
pondération (dBA)	-16,1	-8,6	-3,2	0	+2	+1

1. Donner la définition de la durée de réverbération utilisée dans la formule de Sabine.
2. Calculer le niveau global de puissance acoustique de la source en dB.
3. Compléter le tableau document-réponse puis calculer le niveau de pression acoustique global pondéré en dB_A en un point du bureau.
   -Quel paramètre peut-on chercher à augmenter pour obtenir un niveau conforme aux exigences ? 

fréquence (Hz)	125	250	500	1000	2000	4000
niveau de puissance Lw(dB)	35	42	41	39	36	36
niveau de réverbération T(s)	0,7	0,6	0,6	0,5	0,5	0,4
A (m²)
Lp(dB)
pondération (dBA)	-16,1	-8,6	-3,2	0	2	1

Une pompe hydraulique (cf. schéma ci-dessous) débite 300 m³.h^-1 d'eau froide.

Sa conduite d'aspiration a un diamètre d₁ = 200 mm. Sa conduite de refoulement a un diamètre d₂ = 100 mm.

Dans cette étude toutes les pertes de charge sont négligées.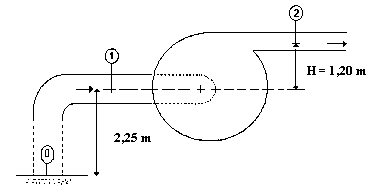

Données :

la masse volumique de l'eau est r₀ = 1000 kg.m^-3 ; g = 9,8 m.s^-2 ; la pression atmosphérique est P₀ = 10⁵ Pa

pour un fluide en écoulement permanent entre 2 points 1 et 2, recevant d'une machine une puissance P, l'équation de Bernoulli est : p₂-p₁+rg(z₂-z₁)+½r(v₂²-v₁²)=P/Q_v.

où Q_v est le débit volumique.

1. Calculer la vitesse d'écoulement V₁ dans la tuyauterie d'aspiration.
2. Calculer la vitesse d'écoulement V₂ dans la tuyauterie de refoulement.
3. La pompe aspire l'eau stagnante d'un bassin ouvert situé 2,25 m au-dessous du niveau (1), d'entrée de la pompe. Calculer la pression p₁ à l'entrée de la pompe, en (1).
4. Calcu1er le débit massique Q_m de la pompe en kg.s^-1.
5. Sachant que la pression de l'eau à la sortie de la pompe, en (2), est p² = 1,60 10⁵ Pa, calculer la puissance mécanique utile P_u fournie par la pompe pour assurer ce débit. Cette pompe est actionnée par un moteur électrique. Le rendement global du groupe est de 80 %. Calculer la puissance électrique P_a consommée.

La fabrication du fer s'effectue dans une tour appelée haut-fourneau. On le charge avec du coke (carbone C) et du minerai de fer dont la teneur massique en oxyde de fer Fe₂O₃ est 20 %. En fin de transformation, on obtient du fer et du dioxyde de carbone. On mélange 30 kg de coke et 10³ kg de minerai de fer.

1. Ecrire et équilibrer l'équation-bilan de la réaction qui se produit dans le haut-fourneau.
2. Calculer les nombres de moles des 2 réactifs présents avant la réaction. Quel est le réactif en excès ?
3. Calculer la masse de fer obtenu lorsque tout l'oxyde de fer a été consommé.
4. Calculer le volume de dioxyde de carbone gazeux dégagé, exprimé en m³.

On donne C=12 ; O=16 ; fe=56 g/mol ; volume molaire des gaz = 24 L/mol.

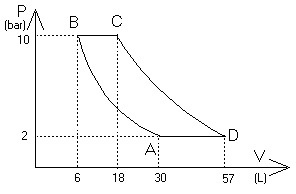
machine thermique :

Une machine thermique met en jeu une masse constante d'un gaz parfait et lui fait décrire le cycle suivant selon des transformations réversibles:

- Une compression isotherme qui fait passer le gaz de l'état A (pression 2 bar; volume 30 L ; température 16°C) à l'état B (P_B; V_B = 6 L ; T_B).

- Un échauffement isobare de l'état B à l'état C (p_C ; V_C = 18 L ; T_C).

- Une détente adiabatique de l'état C à l'état D (p_D ; V_D ; T_D).

- Un refroidissement isobare de l'état D à l'état A.

1. Calculer le nombre de moles gazeuses mises en jeu.
2. Calculer les variables d'état dans les états A, B, C et D.
   -Reproduire dans votre copie, puis compléter, le tableau ci-dessous.

   	pression (Pa)	volume (m3)	température (K)
   état A
   état B
   état C
   état D

3. Représenter ce cycle dans le diagramme de Clapeyron (p, V).
4. Calculer le travail et la quantité de chaleur échangés au cours de la transformation de l'état B à l'état C.

   Données numériques : constante des gaz parfaits: R = 8,31 J.K^-1.mol^-1.

   chaleur molaire à pression constante C_p = 29,1 J.K^-1.mol^-1.

   dans une transformation adiabatique pV^g = constante, avec g = 1,4 pour le gaz considéré.

thermodynamique d'un gaz

Une cuve de 500 L contient du propane C₃H₈ considéré comme un gaz parfait. Elle alimente une chaudière à gaz dont le brûleur a une puissance de 3 kW.

1. La pression est de 10 bars pour une température de 10 °C. Calculer la masse de propane contenue dans la cuve.
2. La nuit, la température descend à – 8 °C. Calculer la pression en bars.
3. Écrire l'équation de combustion complète du propane.
4. On admet que la combustion d'un alcane CnH_2n+2 libère de l'énergie thermique Q qui dépend de la nature de l'alcane. Pour cet alcane, la valeur de Q est de 2220 kJ. mol^-1. Pour une température de 10 °C, la pression dans la cuve est descendue à 8 bars. Calculer l'énergie libérée par la combustion de l'alcane consommé.
5. Calculer la durée de fonctionnement de la chaudière lorsque la pression est de 5 bars pour une température de 10 °C. On donne : M(C)= 12 g.mol^-1 ; M(H) = 1 g.mol^-1

Donnée numérique : constante des gaz parfaits: R = 8,31 J.K^-1.mol^-1.

1. Dans le phénomàne de conduction thermique à travers un matériau :
   - Définir le régime permanent.
   - En utilisant une des deux lois énoncées ci dessous, démontrer que, pour un problème plan, ( mur isotrope homogène, d'épaisseur L, une face à la température q₁ et l'autre à la température q ₂), la courbe de la température q en fonction de l'abscisse x évaluée sur un axe perpendiculaire aux faces du mur, soit q =f(x) est une droite.
2. Un double vitrage comporte deux vitres d'épaisseur L, séparées par une couche d'air d'épaisseur 2L. La température de l'air de la maison est q _0i , celle de l'air extérieur est q _0e < q _0i . La conducrtivité du verre est l_v, celle de l'air est l_a, le coefficient d'échange superficiel sur chacune des faces des vitres en contact avec l'air libre est h. On rappelle qu'il y a convection entre vitres et air libre ( dans la maison et l'extérieur) mais pas entre les vitres et l'air emprisonné.
   - Exprimer littéralement la résistance thermique globale R ( pur 1 m²) en fonction des données.
   - Calculer la densité de flux thermique F à travers l'ensemble.
   q _0i = 20°C ; q _0e = -10°C ; h= 12 Wm^-2 K^-1 ; L=3 mm ; l_v=1,2 W m^-1K^-1 ; l_a=0,024 W m^-1K^-1 ;
3. Calculer les températures des quatre faces des vitres notées q ₁; q '₁, q ₂ et q '₂. Tracer le diagramme des températures q =f(x)

 

---

corrigé

---

les régimes permanents pour lesquels la température en tout point du milieu est indépendante du temps, le déséquilibre est entretenu par les sources de chaleur

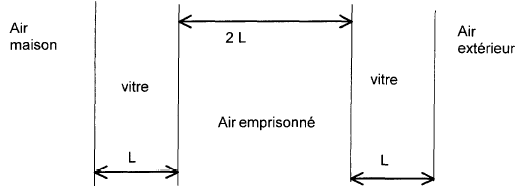
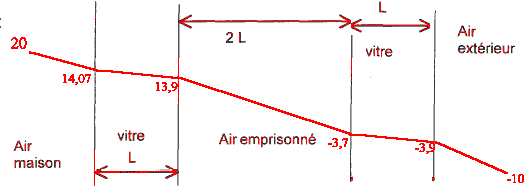
loi de Fourier : le signe - traduit le fait que les échanges tendent à uniformiser la température (autrement dit que spontanément les transferts thermiques se produisent du corps chaud vers le corps froid .

l est appelée conductivité thermique du milieu et traduit l’aptitude à conduire la chaleur.

dq= -j /l dx

intégrer entre deux états noté 1 ( corps chaud) et 2 ( corps froid) : q₂-q₁ = -j /l (x₂-x₁)

(x₂-x₁) représente l'épaisseur , notée e, du milieu homogéne

q₂-q₁ = -j e/l ; q₂= q_froid ; q₁= q_chaud

q_chaud -q_froid = j e/l.

---

résistance thermique R

convection intérieure et extérieure : 1/h+ 1/h = 2/h = 2/12 = 0,167 W^-1m²K

résistance thermique des deux vitres : 2L/l_v = 6 10^-3 / 1,2= 0,005 W^-1m²K

résistance thermique de l'air entre les vitre : 2L/l_a = 6 10^-3 / 0,024= 0,25 W^-1m²K

R= 2/h +2L/l_v + 2L/l_a= 0,167+0,005+0,25= 0,422 W^-1m²K

coefficient de transmission K= 1/R = 1/0,422 = 2,67 Wm^-2K^-1.

flux surfacique F = K(q_chaud -q_froid )=2,67(20-(-10))= 71,1 Wm^-2.

---

températures :

q₁ : q_0i -q₁ = F *1/h= 71,1/12=5,93 soit q₁ = 20-5,93 = 14,07 °C.

q'₁ : q₁ -q'₁ = F *L/l_v= 71,1*3 10^-3/1,2=0,18 soit q'₁ = 14,07-0,18 = 13,89 °C.

q'₂ : q'₁ -q'₂ = F *2L/l_a= 71,1*6 10^-3/0,024=17,78 soit q'₂ = 14,07-17,78 = -3,7 °C.

q' : q'₂ -q₂ = F *L/l_v= 71,1*3 10^-3/1,2=0,18 soit q₂ = 1-3,7-0,18 = -3,88 °C.

---

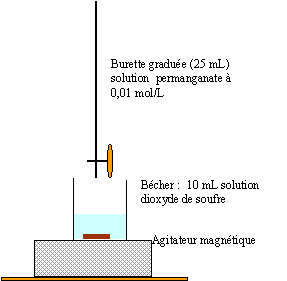
On considére la réaction entre l'ion permanganate MnO₄^- et le dioxyde de soufre SO₂.

couples : MnO₄^- /Mn²⁺ E=1,51 V ; SO₄^2- / SO₂ E=0,17 V

1. Justifier le sens de la réaction spontanée.
   - Equilibrer la demi-équation : MnO₄^- +...H⁺ +...e^--->...Mn²⁺ +...H₂O
   - L'autre demi-équation est : SO₂ + 2H₂O--> SO₄^2- + 4H⁺ + 2e^-. En déduire l'équation complète relative à la réaction entre l'ion permanganate et le dioxyde de soufre.
   - Montrer qu'il faut 2,5 mol de dioxyde de soufre pour 1 mole de permanganate.
2. On utilise cette réaction pour doser 10 mL d'une solution de dioxyde de soufre à l'aide d'une solution de permanganate de potasium dont la couleur violette est uniquement dûe à l'ion permanganate. Il faut verser 20 mL de cette solution pour obtenir l'équivalence.
   - Faire un schéma annoté du dispositif de dosage.
   - Dire comment on repère l'équivalence.
   - Calculer la concentration molaire de la solution de dioxyde de soufre si la concentration de la solution de permanganate de potassium est 0,01 mol/L.