|
doublet de lentilles |
||||
|
||||
|
|
Une petite lunette astronomique afocale est constituée d’un objectif L0 assimilé à une lentille mince convergente, de distance focale f’0 = 320 mm, de diamètre d’ouverture 2R0 = 30 mm et d’un oculaire de grossissement commercial 6,25 composé d’un doublet de lentilles minces L1 et L2 de symbole (3,2,1) I – Etude de l’oculaire (3 points)
II – Caractéristiques de la lunette (9,5 points)
III – Vérification du grossissement (2 points) Afin de vérifier la valeur du grossissement trouvée précédemment, on réalise le montage suivant : 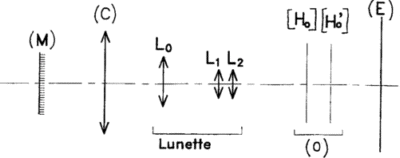 (M) est un micromètre objet gradué en mm et placé dans le plan focal objet de (C) (C) est un collimateur réglé, de distance focale f’C = 500 mm. (O) est un objectif de vergence COB = 5 dioptries qui projette l’image de (M) sur un écran (E) et de distance focale fOB. On constate que 25 mm du micromètre objet M se conjuguent à travers l’ensemble (C), lunette, (O) en une image de 81 mm sur (E)
IV – Transformation de la lunette astronomique en lunette-terrestre (1,5 points) On introduit entre l’objectif L0 et l’oculaire (L1 L2), un bloc de prismes à réflexion totale.
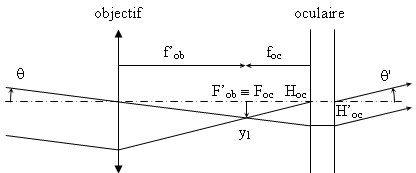
L’oculaire, de grossissement commercial GC= 6,25, a une puissance intrinsèque Pi quatre fois plus grande, donc égale à 25 dioptries, et une focale de 1/25 ème de mètre soit 40 mm. Pi = 4 GC= 4*6,25 = 25 d ; f'= 1/Pi = 1/25 = 0,04m = 40 mm. Si le symbole du doublet est donné par la suite des trois nombres p, q, r, alors : f’1 = p.a e = q.a f’2 = r.a Ici p = 3, q = 2 et r = 1 En reportant dans la première formule de Gullstrand on obtient : 1/f’ = 1/f’1 + 1/f’2 – e/f’1f’2 = 1/(3a) + 1/a – 2a/(3a.a) = (1 + 3 – 2)/(3a )= 2/(3a) Il s’ensuit : a = 2f’/3 = 2 *0,04/3 = 0,08/3 m soit a= 26,67 mm et f’1 = + 80 mm ; e = 53,33 mm ; f’2 = 26,67 mm. La méthode des foyers donne : objet à l'infini - (L1) --> F' 1 - (L2) --> F' et F - (L1) --> F2 - (L2) --> image à infini En appliquant la relation de conjugaison des lentilles minces avec origine au centre optique ( valeurs algébriques pour les distances notées en bleu et en gras) 1/O2F' = 1/O2F'1 +1/f'2 avec O2F'1 = O2O1 + O1F'1 = -53,33 + 80 = -45,3 mm ; f'2 = 26,67 mm O2F' = 13,33 mm. 1/O1F = 1/O1F2 -1/f'1 avec O1F2 = O1O2 + O2F2 = 53,33 -26,67 = 26,66 mm ; f'1 = 80 mm O1F = 40 mm. Le foyer objet F est situé après la première lentille de l’oculaire ; c’est donc un point objet virtuel. En conséquence, l’oculaire est négatif. f'1+f'2 = a(p+r) = a(3+1)=4a = 2*2a=2*qa=2e La condition d’achromatisme apparent est satisfaite (à condition que les deux verres de l’oculaire aient même nombre d’Abbe). Caractéristiques de la lunette Le grossissement de la lunette G est le rapport du diamètre apparent de l’image instrumentale q’ au diamètre apparent de l’objet q. G= q’ / q.
Les angles q’ et q étant supposés petits, leur rapport est égal à celui de leurs tangentes. Si l’on fait un calcul en valeur algébrique avec les conventions usuelles de signe : G= tanq’/tanq=(y1/foc) / (y1/f'ob)= f'ob/foc = 320/(-40)= -8. Le grossissement algébrique négatif indique que l'image est renversée par rapport à l’objet, ou plus précisément que cette image est vue « à l’envers » par l’observateur. Géométriquement, le faisceau issu d’un point objet situé à l’infini dans une direction au dessus de l’axe optique (voir schéma ci-dessus) donne un faisceau image à travers la lunette qui semble, pour l’observateur placé après l’oculaire, provenir d’un point virtuel, éloigné, situé dans une direction en dessous de l’axe optique. D’où la perception d’une image renversée. L’encombrement de l’instrument est défini par la distance qui sépare les lentilles extrêmes : E=L0L2 = L0F'0+ F'0Foc+FocL1+L1L2 = 320+0-40+53,33= 334 mm. Comme l’objet est à l’infini, le demi-champ objet de pleine lumière correspond à la plus grande inclinaison du faisceau utile qui traverse la lucarne d’entrée sans diaphragmation. La pupille d’entrée Pe est le conjugué objet du diaphragme d’ouverture à travers les composants optiques qui le précèdent. Ici, elle est confondue avec l’objectif L0. La lucarne d’entrée Le est le conjugué objet du diaphragme de champ à travers les composants optique qui le précèdent. Ici, le conjugué objet de L1 à travers L0 s’obtient aisément : 1/L0Le = 1/L0L1 -1/f'0=1/(320-40)-1/32d'où L0Le =2240 mm FLe= FL1* L0Le / L0L1 = 20*2240/280 = 160 mm.
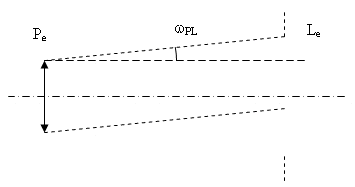
tan wPL= (RLe-RPe) / LePe = (80-15) / 2240 = 0,029 ; wPL= 1,66°. Les champs image et objet sont dans le rapport du grossissement, d’où si l’on suppose les angles petits : w'PL= 8 wPL=13,28°. Le champ de contour peut être éliminé en plaçant dans le plan d’une image réelle un diaphragme et en donnant à celui-ci le diamètre du champ de pleine lumière à cet endroit-là. Les deux images intermédiaires de l’objet sont dans les plans [F’0], confondu avec [Foc], et [F2]. L’oculaire étant négatif, le premier de ces deux plans est virtuel. Il ne peut donc être utilisé. Reste le second plan. Situé entre L1 et L2, il est bien réel. Le champ de pleine lumière en [F2] est le conjugué objet du champ image à travers L2. La relation image/objet fait intervenir la distance focale de L2 : tan w'PL= (RPL2) / f'2 d'où FPL2= 2 f'2tan w'PL=2*26,67 tan 13,28 = 12,6 mm. On place sur le schéma les trois lentilles, les plans (F’0], [F2] et les trois diaphragmes (L0, L1 et PL2 en [F2]). On construit le conjugué objet du bord inférieur b2 de PL2 à travers L1, en joignant ce point au centre optique de L1 et en recherchant l’intersection b1 de ce segment avec [F0]. On trace le faisceau utile à la limite du champ de pleine lumière dans le premier espace intermédiaire en joignant b1 aux bords de L0. La partie du faisceau entre L1 et L2 est virtuelle. Le faisceau coupe le plan de la lentille L1 sur les bords du diaphragme de champ. La direction du faisceau parallèle objet sera obtenue en traçant la droite qui passe par b1 et O1. Le faisceau utile dans le second espace intermédiaire a pour sommet b2 ; il s’appuie sur les bords du diaphragme de champ. Enfin le faisceau image parallèle a pour direction la droite b2O2. La limite de résolution objet due à la diffraction est donnée, en radian, par : LRdiff= 1,22l/(2R0)= 1,22*550 10-6 /30= 2,24 10-5 rad. La limite de résolution due à l’œil estLRoeil=4 10-4 /G= 4 10-4 /8=5 10-5 rad. La limite de résolution de l’association instrument + œil est le plus grand de ces deux résultats, à savoir 5 10-5 rad. Ainsi, c'est l’œil qui limite la résolution de l’ensemble Vérification du grossissement L’objet yC en M donne à travers (C) une image à l’infini de diamètre apparent , tel que q=yC/ f'c La lunette donne de cette image à l’infini une image intrumentale, également à l’infini, de diamètre apparent q ’, tel que q ’= Gq. Enfin, l’objectif de projection donne de l’image instrumentale une image réelle y’ob, telle que : y’ob=f'obq' Les trois équations précédentes donnent la relation demandée : G= |gy|f'c /f'ob avec gy =y’ob/yC Application numérique : G = (81/25)(500/200) = 8,1 Cette valeur est en accord à 1/80e près (incertitude relative de 1,25%) avec la valeur calculée au II.1. Transformation de la lunette astronomique en lunette terrestre Les prismes ont pour fonction : de redresser l’image objective et donc de permettre à l’observateur de voir « à l’endroit » à travers les jumelles ; de réduire l’encombrement longitudinal de l’instrument en repliant les faisceaux lumineux par réflexion. Le champ objet à 1000 m est L = 2 * 1000 * tanwPL = 2 * 1000 * 65 / 2240 = 58 m Le premier nombre
« 8 » correspond au grossissement des jumelles, et le second « 30 », au
diamètre en millimètre de l’ouverture de l’objectif
|
|||
|
Les 3 lentilles composant la lunette sont taillées dans un verre d’indice nV = 1,52. L’épaisseur des lentilles étant faible, l’absorption de la lumière est négligeable et pour chaque dioptre on peut écrire : R + T = 1 avec R le coefficient de réflexion en intensité et T celui de transmission en intensité. Or le coefficient de réflexion en intensité R d’un dioptre éclairé en incidence quasi normale et séparant deux milieux homogènes et isotropes d’indices respectifs n1 et n2 est donné par la formule : R=[(n2-n1)/(n1+n2)]2.
corrigé Pour la lunette comportant 3 lentilles et donc 6 dioptres, TL= T6=0,95746=0,77 soit 77% Le traitement antireflet utilise le principe des interférences destructives. On suppose la lumière monochromatique. Un rayon tombant sur la couche antireflet (AR) est dédoublé en : un rayon (1) réfléchi sur le dioptre air/AR, un rayon (2) réfléchi sur le dioptre AR/verre. Compte-tenu de la petitesse de l’épaisseur de l’antireflet, la différence de marche entre ces deux rayons est très faible (inférieure de toute façon à la longueur de cohérence). Ils peuvent interférer. Les interférences sont destructives si les vibrations (1) et (2) sont en opposition de phase. L’intensité vibratoire est alors minimum. Le reflet est totalement éteint si, de plus, les amplitudes des deux vibrations sont égales. La première condition définit l’épaisseur de l’antireflet, et la seconde son indice de réfraction. L’antireflet est optimisé pour un angle d’incidence donné (en général 0°) et une longueur d’onde particulière. En lumière polychromatique et incidence oblique, les performances de l’antireflet diminuent. L’indice théorique du matériau idéal serait : nM= racine carrée (nV)= racine carrée (1,52) = 1,23. Comme les indices vont croissant, de l’air vers le verre (1 c v), les deux réflexions sont de même nature et la différence de marche, en incidence normale est : d= 2ncec. Comme les vibrations sont en opposition de phase, F=(2k+1) p. La relation entre déphasage et différence de marche étant F=2 p d/l, la condition d’épaisseur s’écrit : ec=(2k+1)l/(4nc) La première solution (k = 0) est choisie, car c’est celle qui donne la meilleure efficacité de l’antireflet en lumière polychromatique et incidence oblique. ec=560/(4*1,35)=103,7 nm.
|
||||
| |
||||
|
|