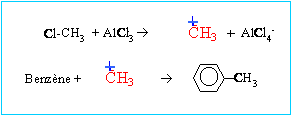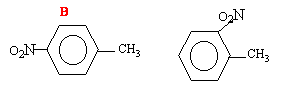Aurelie juin 04

spectrophotométrie - radioactivité - pile Daniell - chimie organique

d'après BTS biochimiste 03



Google



spectrophotométrie

A l'aide d'un spectrophotomètre, on réalise une série de mesures d'absorbance A de solutions de violet cristallisé, àla longueur d'onde l= 580 nm. La cuve a une épaisseur l =1 cm. On obtient les résultats suivants en fonction de la concentration massique r des solutions :
r gL-1
0,6 10-3
1,5 10-3
2,4 10-3
3 10-3
4,5 10-3
6 10-3
A
0,075
0,25
0,42
0,515
0,775
1,04
Données : violet cristallisé C25H30N3 ; M=408,19 g/mol

  1. Définir la transmittance T et l'absorbance Ad'une solution.
  2. Enoncer la loi de Berr-Lambert; expliciter tous ces termes et donner leurs unités.
  3. Quel est le critère de choix de la longueur d'onde à laquelle s'effectue les mesures ? Pourquoi ?
  4. Montrer que la loi de Berr est vérifiée pour cette série de solutions.
  5. Déterminer la valeur du coefficient d'absorption molaire du violet cristallisé.
  6. La mesure de l'absorbance d'une solution de violet cridtallisé de concentration inconnue, réalisée dans ces conditions, donne A= 0,531. Déterminer la concentration molaire c et la concentration massique r de cette solution.
corrigé
La transmission T est définie comme le rapport de l'intensité transmise I à l'intensité incidente I0.

T = I / I0 ; log T= -A.

A= log (I0/I) = elc ( A est l'absorbance ou densité optique)

où e est un coefficient caractéristique de la substance appelé coefficient d'absorbance (L mol-1 cm-1), l est l'épaisseur de la cuve (cm) et c la concentration de la solution (mol/L).

Les solutions colorées présentent une longueur d’onde lumineuse où l’absorption est maximale. Cette longueur d’onde maximale l max ne dépend pas de la concentration, c’est une grandeur caractéristique de l’ion absorbant. Elle est utilisée pour effectuer les mesures photométriques sur des solutions de différentes concentrations.
r gL-1
0,6 10-3
1,5 10-3
2,4 10-3
3 10-3
4,5 10-3
6 10-3
A
0,075
0,25
0,42
0,515
0,775
1,04
r /A gL-1
8 10-3
6 10-3
5,7 10-3
5,8 10-3
5,8 10-3
5,76 10-3
r /A étant à peu près constant, la loi de Beer est vérifiée.

r /A = 5,8 10-3 g L-1.

C/A=5,8 10-3 / masse molaire (g/mol) = 5,8 10-3 /408,19 =1,42 10-5 mol/L = 1,42 10-2 mol m-3.

r /A = 1 /(el) avec largeur l = 10-2 m ;

1,42 10-2 = 1/(10-2 e ) = 100 / e soit e = 100 /1,42 10-2 = 104 /1,42 =7042 m2 mol-1.

ou bien : 1,42 10-5= 1/(1* e ) soit e = 1/1,42 10-5=70420 Lmol-1 cm-1.

si A= 0,531 alors C/A= 1,42 10-5 mol/L soit C= 0,531*1,42 10-5 = 7,54 10-6 mol/L

r = 7,54 10-6*408,19 =3,08 10-3 g/L.

 

radioactivité

Le 3215P est un isotope radioactif du phosphore émetteur b-, de période T=14 jours. Il est utilisé dans le traitement de certaines pathologies du sang ; la dose thérapeutique est de 4 106 Bq par kg de masse corporelle à 10% près.

  1. Ecrire la réaction de désintégration radioactive. Préciser les lois de conservation.
  2. Montrer que la constante radioactive l vaut 4,95 10-2 j-1. L'exprimer en s-1.
  3. Quelle doit être l'activité d'une gélule renfermant cet isotope, destinée à traiter un patient de 90 kg ? En déduire le nombre d'atomes de 3215P contenus dans cette gélule, puis la masse corespondante.
  4. On a préparer à un jour donné J0 une capsule d'activité A0=4 108 Bq qui par la suite d'un contre temps n'a pas été utilisée. Calculer son activité A au bout de 10 jours J10. Peut-elle encore être utilisée à J10 pour traiter une patiente de 58 kg ?

Données : nombre d'Avogadro NA= 6,02 1023 ; 13Al ; 14Si ; 15P ; 16S ; 17Cl ; 18Ar.

corrigé
3215P ->3216S + 0-1e

conservation du nombre de nucléon : 32 = 32+0

conservation de la charge : 15= 16-1

lT=ln2 =0,693 soit l =0,693 / T = 0,693 / 14 = 4,95 10-2 j-1.

14 j = 14*24*3600 s =1,21 106 s ; l = 0,693 / 1,21 106 =5,73 10-7 s-1.

activité pour un patient de 90 kg : 90*4 106 = 3,6 108 Bq

nombre d'atomes de 3215P correspondant : A= l N soit N=A/ l.

N= 3,6 108 / 5,73 10-7 = 6,28 1014 atomes

Qté de matière en mol : 6,28 1014 / NA= 6,28 1014 / 6,02 1023= 1,04 10-9 mol

masse de 3215P : Qté de matière * masse molaire (g/mol) = 1,04 10-9 *32 = 3,34 10-8 g.

A= A0 e-lt ; avec l t = 4,95 10-2*10 =0,495 et A10 = 3,6 108 e(-0,495)=2,19 108 Bq.

pour une patiente de 58 kg : A= 4 106*58 = 2,3 108 Bq

la capsule précédente peut être utilisée.

pile daniell

 On étudie à 25°C, l'équilibre mis en jeu dans la pile Daniell Zn(s) + Cu2+ = Cu(s) + Zn2+.

  1. A partir des données thermodynamiques ci-dessous, déterminer l'enthalpie standart DfH0, l'entropie standart DfS0, et l'enthalpie libre standart DfG 0 de la réaction à 298 K.
    - Quel est le sens de la réaction spontanée à l'étatt standart ? Justifier.
    T=298 K
    Zn(s)
    Cu(s)
    Zn2+
    Cu2+
    DfH0 kJ/mol
    0
    0
    -153,4
    65,7
    S0 Jmol-1 K-1
    41,6
    33,2
    -109,6
    -97,1
  2. Calculer la constante d'équilibre K. Conclure.
  3. On donne à 25°C les potentiels standarts des deux couples : E0Cu2+/Cu = 0,34 V ; E0Zn2+/Zn = -0,76 V.
    - Ecrire l'équation de la réaction spontanée entre les deux couples dans les conditions standart. Justifier.
    - Est-ce en accord avec la réponse à la quaestion 1 ?
  4. Calculer a force électromotrice de la pile E0.
    On rappelle la constitution d'une pile daniell : - Zn(s) / ZnSO4 // CuSO4 / Cu(s) +
    En déduire l'enthalpie libre standart DfG0 à 298 K de la réaction précédente. Comparer avec le résultat de la question 1.

R= 8,31 J K-1 mol-1 ; 1F = 96500 C

corrigé
DfH0 = DfH0(Zn2+)- DfH0(Cu2+)= -153,4-65,7= -219,1 kJ/mol= -219,1 103J/mol

DfS0 = S0 (Zn2+) + S0 (Cu)-S0 (Cu2+)-S0 (Zn)= -109,6+33,2-(-97,1)-41,6 = -20,9 Jmol-1 K-1

DfG 0 = DfH0-TDfS0 = -219,1 103-298*(-20,9)= -212,87 103 J/mol = -212,87 kJ/mol

affinité A = -DfG 0 =212,87 kJ/mol

l'affinité étant positive, la réaction évolue spontanément dans le sens direct, de gauche à droite.

constante d'équilibre K= [Zn2+]éq/[Cu2+]éq

A= RT lnK soit ln K=A/(RT)= 212,87 103 / (8,31*298)=85,96

K= 2,15 1037 valeur très grande, donc la réaction est totale

le réducteur le plus fort appartient au couple ayant le plus petit potentiel.

le zinc est le réducteur le plus fort et l'ion cuivre II constitue l'oxydant le plus fort

le zinc s'oxyde : Zn (s)= Zn2+ + 2 électrons

l'ion cuivre II se réduit Cu2+ + 2électrons = Cu(s)

Zn(s) + Cu2+ = Cu(s) + Zn2+.

fem standart E0 =E0Cu2+/Cu - E0Zn2+/Zn =0,34 -(-0,76 )= 1,1V.

- DfG 0 = nFE0 ;

DfG 0 = -nFE0 = -2 *96500*1,1 = -2,12 105 J/mol = -212,3 kJ/mol

en accord avec la valeur de la question 1.

Chimie organique

On fait réagir du benzène avec du monochlorométhane en présence de chlorure d'aluminium AlCl3.

  1. Ecrire l'équation de la réaction. On appelle A le composé organique obtenu. Donner son nom
    - De quel type de réaction s'agit-il ?
    - Donner les différentes étapes de son mécanisme.
  2. On réalise la mononitration de A. Quel réactifs utilise-t-on pour effectuer cette réaction ?
    - Ecrire l'équation de la réaction et justifier l'obtention d'un mélange de deux isomères.
    - Donner la formule de l'isomère B majoritairement obtenu.
  3. On oxyde B par le permanganate de potassium en milieu acide. Ecrire les deux demi-équations électroniques puis l'équation de la réaction d'oxydoréduction.
    Les couples redox mis en jeu sont : NO2-C6H4-COOH / B et MnO4-/Mn2+.
corrigé
C6H6 +CH3Cl -->C6H5 -CH3 + HCl

C6H5 -CH3 : méthylbenzène

réaction de Friedel et Crafts, substitution électrophile sur le benzène

On utilise le mélange sulfonitrique ( permet de préparer NO2+) pour une nitration.

le groupe méthyl auglmente la densité électronique en ortho et en para ; on obtient donc deux isomères

le dérivé para est majoritaire ; le dérivé ortho est minoritaire ( gène stérique entre CH3 et NO2)

6 fois {MnO4- + 8H+ + 5e- = Mn2+ + 4H2O} réduction de l'oxydant

5 fois { NO2-C6H4-CH3 + 2H2O= NO2-C6H4-COOH + 6H+ + 6e-}oxydation du réducteur.

6 MnO4- + 18 H+ + 5 NO2-C6H4-CH3 = 6 Mn2++5 NO2-C6H4-COOH + 14 H2O


retour -menu